

Ο Αρχιμήδης έδωσε δύο λύσεις στο πρόβλημα της τριχοτόμησης της γωνίας. Η μία παρουσιάζεται παρακάτω.
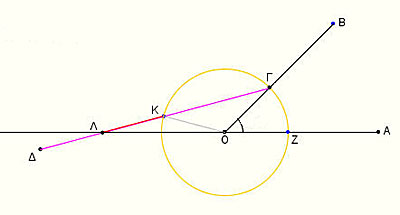
Έστω ΑΟΒ η γωνία που θέλουμε να τριχοτομήσουμε. Γράφουμε ένα κύκλο με κέντρο την κορυφή Ο της γωνίας και έστω Γ το σημείο στο οποίο τέμνει την πλευρά της ΟΒ. Σχεδιάζουμε το τμήμα ΓΛ ώστε το τμήμα ΚΛ
να είναι ίσο με την ακτίνα του κύκλου και τότε η γωνία ΚΛΟ είναι ίση με το ένα τρίτο της ΑΟΒ.
Πράγματι, το τρίγωνο ΚΛΟ είναι ισοσκελές άρα `hat(KLambdaO)=hat(LambdaOK)` (1)
Όμοια το ΚΟΓ είναι ισοσκελές άρα, `hat(OKGamma)=hat(OGammaK)` (2). Η γωνία ΟΚΓ είναι εξωτερική του τριγώνου ΚΛΟ άρα λόγω της σχέσης (1) είναι, `hat(OKGamma)=2hat(KLambdaO)` (3). Η γωνία ΑΟΒ είναι εξωτερική του τριγώνου ΓΟΛ άρα λόγω της (2) και της (3) θα είναι, `hat(AOB)=3hat(KLambdaO)`
Το πρόβλημα είναι ότι, η ΓΛ δεν μπορεί να σχεδιαστεί με κανόνα και διαβήτη, ώστε το ΚΛ να είναι ίσο με την ακτίνα του κύκλου. Η σχεδίαση της ΓΛ μπορεί να γίνει με το παρακάτω όργανο
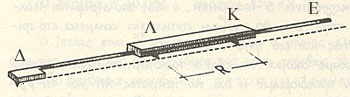
στο οποίο ο ιππέας ΚΛ μπορεί να κινείται πάνω στην ΕΔ. Το όργανο αυτό προσομοιώνουμε στην παρακάτω εφαρμογή.(διαβάστε τις οδηγίες για την λειτουργία του οργάνου και ακολουθήστε τις υποδείξεις στο κάτω μέρος)