

Ο Πάππος στο έργο του "Μαθηματική συναγωγή" έδωσε δύο λύσεις στο πρόβλημα της τριχοτόμησης μιας γωνίας. Τη μία από αυτές παρουσιάζουμε παρακάτω.
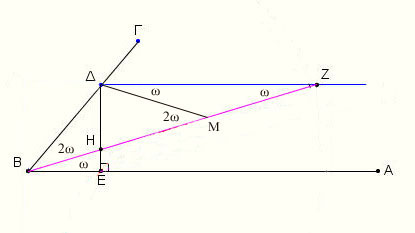
Έστω ΑΒΓ η γωνία που θέλουμε να τριχοτομήσουμε. Από ένα σημείο Δ της ΒΓ φέρουμε την ΔΕ κάθετη στη ΒΑ και την παράλληλη στην ΒΑ. Θεωρούμε το ευθύγραμμο τμήμα ΗΖ τέτοιο ώστε να είναι ΗΖ=2ΒΔ και η προέκταση του να διέρχεται από το Β.Τότε η γωνία ΖΒΑ είναι ίση με το ένα τρίτο της ΑΒΓ.
Πράγματι αν Μ το μέσο της υποτείνουσας ΗΖ του ορθογωνίου τριγώνου ΗΔΖ, θα είναι ΗΜ=ΜΖ=ΔΜ και επειδή ΗΖ=2ΒΔ θα είναι ΒΔ=ΔΜ=ΜΖ=ΜΗ.
Η γωνία ΔΖΒ=ΖΒΑ λόγω των παραλλήλων ΔΖ//ΒΑ, η γωνία ΜΔΖ=ΜΖΔ επειδή το τρίγωνο ΜΔΖ είναι ισοσκελές.
Η γωνία ΔΜΒ είναι εξωτερική του τριγώνου ΜΔΖ, άρα θα είναι 2ω και η ΔΒΜ=2ω από το ισοσκελές τρίγωνο ΒΔΜ.
Έτσι η γωνία ΑΒΓ είναι ίση με 3ω, άρα η ω είναι το ένα τρίτο της ΑΒΓ δηλ η γωνία τριχοτομήθηκε.
Το πρόβλημα τώρα είναι, πως θα κατασκευάσουμε το τμήμα ΗΖ ώστε, να έχει τα άκρα του πάνω στις γνωστές ευθείες ΔΕ και ΔΖ να έχει μήκος 2ΒΔ και η προέκταση του να διέρχεται από το Β. Το πρόβλημα
αυτό, της κατασκευής ενός τμήματος με δεδομένο μήκος του οποίου να άκρα να βρίσκονται σε γνωστές γραμμές και το ίδιο ή προεκτεινόμενο να διέρχεται από γνωστό σημείο, ήταν γνωστό στους αρχαίους ως κατασκευή
νεύσεως ή απλά νεύσις .
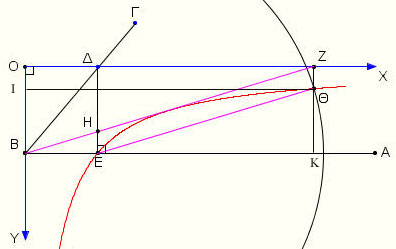
Ας υποθέσουμε ότι κατασκευάσαμε το παραπάνω τμήμα ΗΖ και ας θεωρήσουμε ένα ορθογώνιο σύστημα συντεταγμένων με τον άξονα ΟΧ πάνω στην ΔΖ και τον ΟΥ να διέρχεται από το Β. Φέρουμε την ΖΚ κάθετη στον ΟΧ , από το Ε την παράλληλη στην ΒΖ η οποία τέμνει την ΖΚ στο Θ και την ΘΙ κάθετη στον ΟΥ.
Τα τρίγωνα ΒΗΕ και ΗΔΖ είναι όμοια, άρα ισχύει η σχέση
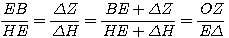 (1).
(1).
Από την (1) προκύπτει η ΗΕ·ΟΖ =ΕB·ΕΔ και επειδή ΗΕ=ΘΖ και ΟΖ=ΘΙ έχουμε ΘΖ·ΘΙ=ΕΒ·ΕΔ (2) .
Αν (x,y) είναι οι συντεταγμένες του Θ ως προς το σύστημα ΟΧΥ θα είναι x =ΘΙ και y=ΘΖ και λόγω της (2) έχουμε x·y = c (3) , όπου c το σταθερό
γινόμενο ΕΒ·ΕΔ .
Από την (3) προκύπτει ότι, το σημείο Θ ανήκει σε μια γνωστή υπερβολή και επειδή ΕΘ =ΗΖ=2ΒΔ θα ανήκει επίσης και στον κύκλο με κέντρο το Ε και ακτίνα 2ΒΔ, έτσι το σημείο Θ κατασκευάζεται ως τομή της υπερβολής και του κύκλου.