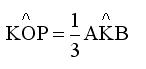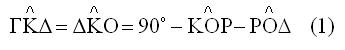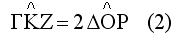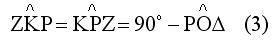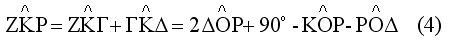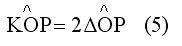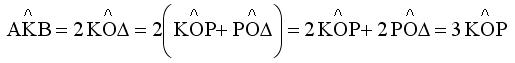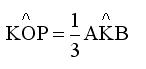Τριχοτόμηση Γωνίας -Η λύση του Blaise Pascal
Για να λύσει το πρόβλημα της τριχοτόμησης της γωνίας, ο
Pascal
χρησιμοποίησε την κοχλιοειδή καμπύλη που επινόησε ο πατέρας του .Η καμπύλη αυτή ορίζεται ως εξής. Θεωρούμε ένα κύκλο κέντρου Κ και πάνω σ' αυτόν ένα σημείο Ο το οποίο ονομάζουμε πόλον .Έστω ένα κινητό
σημείο Μ του κύκλου ,πάνω στην ΟΜ και εκατέρωθεν του Μ παίρνουμε δύο σημεία Ρ και Λ ώστε ΜΡ=ΜΛ=α ,όπου α δοθέν τμήμα. Όταν το Μ κινείται πάνω στον κύκλο τα Ρ και Λ γράφουν την κοχλιοειδή καμπύλη. Στο
διπλανό σχήμα μπορείτε να την σχεδιάσετε.
Ο Pascal παρατήρησε ότι στην ειδική περίπτωση πού πάρουμε το τμήμα α ίσο με την ακτίνα του κύκλου μπορούμε να τριχοτομήσουμε μια γωνία όπως περιγράφεται παρακάτω .Διαβάστε τις οδηγίες για το σχηματισμό
του σχήματος
Για την απόδειξη των παραπάνω έχουμε:
Επειδή η ΚΔ είναι κάθετη στη ΟΓ είναι
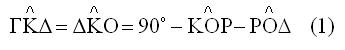
Η ΓΚΖ γωνία είναι επίκεντρη και βαίνει στο ίδιο τόξο με την εγγεγραμμένη ΓΟΖ άρα θα είναι
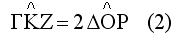
Το σημείο Ρ ανήκει στην κοχλιοειδή καμπύλη άρα ΖΡ=ΖΚ δηλ το τρίγωνο ΡΚΖ είναι ισοσκελές και επειδή η γωνία ΚΡΖ είναι κατακορυφήν με την ΔΡΟ θα είναι
Είναι επίσης
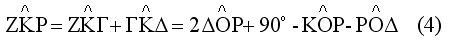
Εξισώνοντας τα δεύτερα μέλη των (3) και (4) προκύπτει
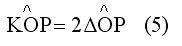
Η γωνία ΑΚΒ είναι εξωτερική στο ισοσκελές τρίγωνο ΟΚΓ άρα ισχύει λόγω και της (5).
Άρα