-
Step 1 (The tunnel of Eupalinos)
Let’s know an early technological masterpiece.
In the middle of the 5th century B.C., Samos, a Greek island, had developed trade, navigation, education and arts. The `tyrant' of Samos, Polycrates, engaged the engineer Eupalinos to carry out various public works.
One of these was to build a tunnel. The northern walls of the town ran along a mountain ridge about 250-300 metres high, and at the western extremity of this small mountain there was a spring on the north side, called Agiade today. Polycrates wanted the water piped into the town. Eupalinos organised the work so that the tunnel was begun from both sides of the hill and the two teams met in the middle. The estimates for the time required range from 5 to 15 years: the mountain is solid limestone and one has to suppose that many of the slaves doing the work died. The tunnel's existence was recorded by Herodotus (as was the mole and harbour, and the third wonder of the island, the great temple to Hera, thought by many to be the largest in the Greek world). The tunnel is 1,046 meters (3,150 feet) long and it is dug on a north-to-south direction. It is located at an altitude of 55 meters (165 feet) and buried 180 meters (540 feet) under the peak of mount Kastros.
The method Eupalinos employed to make the two groups meet in the middle of the mountain. In planning the digging, Eupalinos used what are now well-known principles of geometry, which were codified by Euclid several centuries later. Eupalinos was aware that mistakes in measurement could make him miss the meeting point of the two teams, either horizontally or vertically.The intellectual feat of determining the direction of tunnelling was equally impressive.
- But how did Eupalinos found the distance?
- Did the Pythagorean Theorem help him?
See the video first
and visit this site below
http://calteches.library.caltech.edu/689/2/Samos.pdf
to answer the questions on your sheet of paper. Step 2 (Pythagorean Theorem)
The class will be separated in 4 groups.
Each member of the group will take on a different responsibility.
Choose in your group who will take on each role and after discuss the information you have collected within the group.
All the groups will present their assignment to the class.- First Role: Biographer
Let’s find out who Pythagoras was and what was the theorem named for him.
- Answer the following questions.
- Where was Pythagoras born? Did he live there all his life?
- What three pursuits did Pythagoras dedicate his life to?
- According to Pythagoras, how could the world be understood?
- What does his most famous contribution state?
- In what other science did the make a contribution? What did he state?
The answers can be found by looking through the internet:
- Second Role: Young Scientist
Let’s prove the Pythagorean Theorem.
The following links have different proofs of the theorem. Choose one you understand and explain it to the class.
- http://sunsite.ubc.ca/LivingMathematics/V001N01/UBCExamples/Pythagoras/pythagoras.html
- http://www.cut-the-knot.org/pythagoras/index.shtml
- http://www.pbs.org/wgbh/nova/proof/puzzle/
- Third Role: Daily Mathematician
Let’s present some daily math problems.
Here are some ideas about the types of problems you could solve and applications of the Pythagorean Theorem to real life situations.- Visit the following links and find some applications of the Pythagorean Theorem, in the “real world”:
- Visit the following URLs and solve some problems using the Pythagorean Theorem:
- http://www.geom.uiuc.edu/~hipp/app1b.html
- http://www.yteach.com/page.php/resources/view_all?id=pythagoras_theorem_side_triangle_angle_diagonal_rhombus_rectangle_trapezium_equilateral&from=search
- Pythagorean Shoe Laces (pdf file)
Original file from http://www.mymaths.co.uk/integrate/file.asp?section=Shape&fileID=1870§ionID=3&topic=pythagoras
-
Try to fix 3 of the below applets. Is it difficult?
http://www.ies.co.jp/math/java/geo/pythagoras.html
- First Role: Biographer
-
Step 3 (Exercise)
Step 4 (Game)
Let’s play our game. Are you ready to answer to our story?
Every group work separately.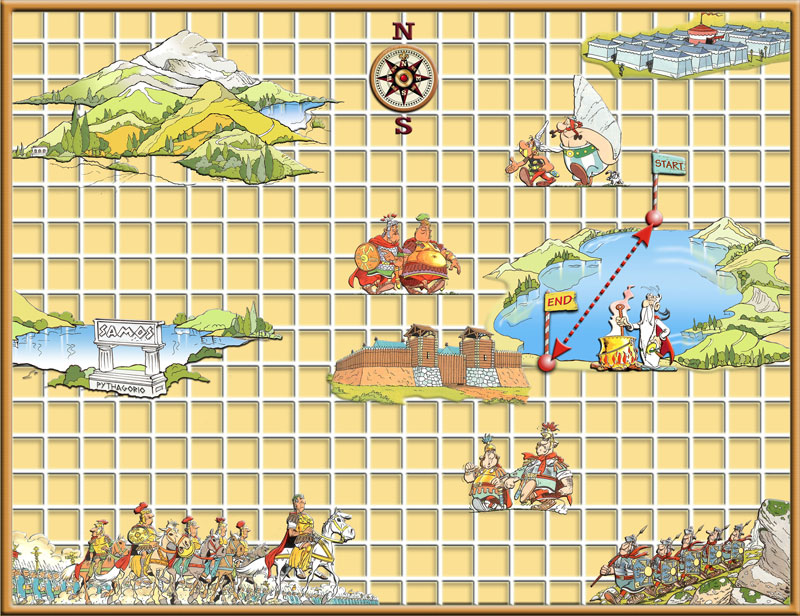
-
Instructions – Directions:
- There are two points on the map: start point START and end point END
- The aim of the game is to calculate the distance START - END without using a measuring tape
- You can move right or left, up or down but not diagonally avoiding obstructions, in order to get from point START to point END
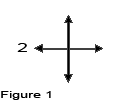 Every time you move up, down, left or right, you should note on the scheme the alteration of your movement
Every time you move up, down, left or right, you should note on the scheme the alteration of your movement
E.g.: If you move 2 squares to the left ( 2 squares west ) , mark 2 as you can see in the figure 1
-
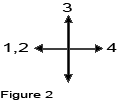 In the same way continue, always marking in the figure, the alternation of every movement
In the same way continue, always marking in the figure, the alternation of every movement
E.g.: After the first movement, you have made the following movements: 3 squares up, 4 squares to the right and one square to the left. You must have noted the following as you can see in the figure 2:
- After you have reached end point END, sum up the number on each direction
E.g. : If you have total movement to the left 6 and to the right 4 , then the total movement is 2 ( 6 – 4 = 2 ) , to the left - Do the same for the other two directions
- In that way you get to two directions with the respective numbers
- These are the lengths of the two vertical sides of the right- angle triangle of witch the hypotenuse is the distance we want to calculate
- Apply the Pythagorean Theorem and find the distance START - END
EXAMPLE
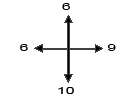
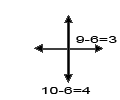
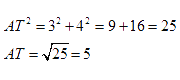
You can follow any route you want … The result will be the same
Process
You will be given 4 class periods to conduct your research on the Internet, and complete this part of the project.