-
Βήμα 1 (Το Ευπαλίνειο όρυγμα)
Ας γνωρίσουμε ένα πρώιμο τεχνολογικό επίτευγμα.
Στα μέσα του 5ου αιώνα π.Χ., το ελληνικό νησί της Σάμου, είχε αναπτύξει το εμπόριο, τη ναυσιπλοΐα, την εκπαίδευση και τις τέχνες. Ο «τύραννος» της Σάμου, ο Πολυκράτης, ζητούσε από τον μηχανικό Ευπάλινο να εκτελέσει διάφορα δημόσια έργα.
Ένα από αυτά ήταν η κατασκευή μιας σήραγγας. Τα βόρεια τείχη της πόλης ήταν χτισμένα κατά μήκος μιας κορυφογραμμή, περίπου 250-300 μέτρα ύψος, και στο δυτικό άκρο αυτού του μικρού βουνού, στη βόρεια πλευρά, υπήρχε μια πηγή που σήμερα ονομάζεται Αγιάδες. Ο Πολυκράτης ήθελε το νερό από την πηγή να μεταφερθεί στην πόλη της Σάμου. Ο Ευπαλίνος οργάνωσε τις εργασίες με τέτοιο τρόπο ώστε η σήραγγα να ξεκινήσει και από τις δύο πλευρές του λόφου και οι δύο ομάδες εκσκαφής συναντήθηκαν στη μέση. Οι εκτιμήσεις για το χρόνο που απαιτήθηκε για τη διάνοιξη της σήραγγας κυμαίνεται από 5 έως 15 έτη: το βουνό είναι από ασβεστόλιθο και μπορεί κανείς να υποθέσει ότι πολλοί από τους σκλάβους που δούλεψαν στην κατασκευή της σήραγγας πέθαναν. Η ύπαρξη της σήραγγας καταγράφηκε από τον Ηρόδοτο. Η σήραγγα έχει μήκος 1.046 μέτρα (3.150 πόδια) και είναι σκαμμένη από βορρά προς νότο. Βρίσκεται σε υψόμετρο 55 μέτρων (165 πόδια) και σε βάθος 180 μέτρα (540 πόδια) κάτω από την κορυφή του όρους Κάστρου
Η μέθοδος - τεχνική που χρησιμοποίησε ο Ευπάλινος για να κάνει τις δύο ομάδες που έσκαβαν να συναντηθούν στη μέσο του βουνού (πράγμα ακόμα και σήμερα πολύ δύσκολο), βασίστηκε σε γνωστές αρχές της γεωμετρίας, οι οποίες κωδικοποιήθηκαν από τον Ευκλείδη δύο αιώνες αργότερα. Ο Ευπαλίνος γνώριζε ότι ένα λάθος στη μέτρηση θα μπορούσε να χάσει το σημείο συνάντησης των δύο ομάδων, είτε οριζόντια είτε κατακόρυφα. Επίσης ο καθορισμός της κατεύθυνσης / κλίσης της σήραγγας ήταν επίσης εντυπωσιακός.
Τα ερωτήματα που θα πρέπει να απαντήσετε είναι δύο:- Πώς υπολόγισε ο Ευπάλινος την απόσταση;
- Το Πυθαγόρειο θεώρημα τον βοήθησε;
1. Δείτε τα βίντεο που ακολουθούν για να μάθετε περισσότερα και να καταλάβετε την τεχνική του Ευπάλινου
2. Αν θέλετε επιπλέον βοήθεια για να παρακολουθήσετε τη σκέψη του Ευπάλινου επισκεφθείτε τον παρακάτω σύνδεσμο:http://calteches.library.caltech.edu/689/2/Samos.pdf
3. Αν ακόμα έχετε απορίες διαβάστε το παρακάτω κείμενο:
Ένα από τα προβλήματα που αντιμετώπισε ο Ευπαλίνος για την κατασκευή της σήραγγας, ήταν ο ακριβής προσδιορισμός του μήκους αυτής πριν την διάνοιξη.
Αυτό έγινε με τον παρακάτω γεωμετρικό τρόπο:
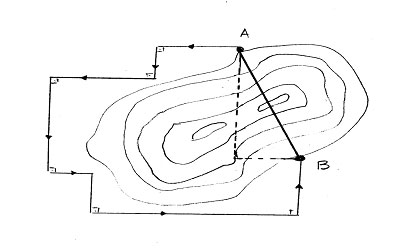
Έχοντας προσδιορίσει τα δυο άκρα της σήραγγας Α, Β τα οποία βρίσκονταν στο ίδιο υψόμετρο άρχισε να μετακινείται από το Α προς το Β σε οριζόντιες και κάθετες διευθύνσεις υπολογίζοντας πάντα αυτές τις αποστάσεις σε οριζόντιο επίπεδο χρησιμοποιώντας την διόπτρα για την οριζόντια σκόπευση.
Βρίσκοντας το αλγεβρικό άθροισμα των οριζόντιων, κάθετων μετακινήσεών του υπολόγισε τις κάθετες πλευρές ενος νοητού ορθογωνίου τριγώνου που είχε υποτείνουσα την απόσταση ΑΒ (μήκος της σήραγγας).
Σύμφωνα λοιπόν με το Πυθαγόρειο θεώρημα έχοντας τα μήκη των καθέτων πλευρών του ορθογωνίου τριγώνου ο υπολογισμός του μήκους της υποτείνουσας (μήκος σήραγγας) ήταν πλέον εφικτός.
Βήμα 2 (Πυθαγόρειο Θεώρημα)
Η τάξη θα χωριστεί σε 4 ομάδες.
Κάθε μέλος της ομάδας θα πάρει ένα διαφορετικό ρόλο. Επιλέξτε στην ομάδα σας ποιoς θα αναλάβει τον κάθε ρόλο και μετά συζητείστε τις πληροφορίες που έχετε συλλέξει στο πλαίσιο της ομάδας.
Όλες οι ομάδες θα παρουσιάσουν την εργασία τους στην τάξη.- Πρώτος ρόλος: βιογράφος
Ας μάθουμε ποιος ήταν ο Πυθαγόρας και ποιο ήταν το θεώρημα που πήρε το όνομά του από αυτόν.
- Απαντήστε στις παρακάτω ερωτήσεις:
- Πού γεννήθηκε ο Πυθαγόρας; Έζησε εκεί όλη του τη ζωή;
- Μελετείστε και καταγράψτε συνοπτικά τουλάχιστον τρία επίπεδα δράσης στα οποία αφιέρωσε τη ζωή του ο Πυθαγόρας;
- Ποια ήταν η συμβολή του στα Μαθηματικά;
Οι απαντήσεις θα δοθούν μετά από την μελέτη των παρακάτω πηγών στο Διαδίκτυο:- http://el.wikipedia.org/wiki/Πυθαγόρας
- http://hellas.teipir.gr/thesis/samos/greek/pythagoras.html/
- http://vod.sch.gr/asx/science/mathematics/
- Δεύτερος ρόλος: Μικρός επιστήμονας
Ας αποδείξουμε το Πυθαγόρειο θεώρημα.
Οι παρακάτω σύνδεσμοι έχουν διαφορετικές αποδείξεις του θεωρήματος. Επέλεξτε μια απόδειξη και εξηγήστε την αρχικά στην ομάδα και κατόπιν στην τάξη.
- http://www.walter-fendt.de/m14gr/pyththeorem_gr.htm
- http://users.sch.gr/geoman22/b-gym/b-1/b-1-4a.htm
- http://grmath4.phpnet.us/mathimatika/pyth_theorhma_megtheor/pythagoreio_thewrhma.htm
- http://users.sch.gr/thafounar/Genika/Pyth-Hui/hui.htm
- http://users.sch.gr/thafounar/Genika/PythagorioTheorima/PythagorioTheorima.htm
- http://users.sch.gr/thafounar/Genika/PythagorioTheorima/apodPythagora.html
- http://www.zosimaia.gr/?page=article&id=257
- http://users.sch.gr/thafounar/Genika/PythagorioTheorima/PythagorasApo.htm
- Τρίτος ρόλος: Καθημερινός Μαθηματικός
Ας παρουσιάσουμε μερικά μαθηματικά προβλήματα στην καθημερινή μας ζωή.
Στους παρακάτω συνδέσμους θα βρείτε μερικές ιδέες από την πραγματική ζωή σχετικά με τα είδη των προβλημάτων που θα μπορούσαν να λυθούν εφαρμόζοντας το Πυθαγόρειο θεώρημα.- Επισκεφθείτε τις παρακάτω ιστοσελίδες και συναντείστε κάποιες από τις πολλές εφαρμογές του Πυθαγορείου θεωρήματος, στον "πραγματικό κόσμο":
- Επισκεφθείτε τις παρακάτω ιστοσελίδες και λύστε κάποια προβλήματα χρησιμοποιώντας το Πυθαγόρειο θεώρημα:
-
Προσπαθήστε να δουλέψετε σε 3 τουλάχιστον από τα παρακάτω applets. Είναι δύσκολο;
Applets πυθαγόρειο θεώρημα
- Πρώτος ρόλος: βιογράφος
-
Βήμα 3 (Άσκηση)
Βήμα 4 (Το παιχνίδι)
Ας παίξουμε το παιχνίδι μας. Είστε έτοιμοι να απαντήσετε στην ιστορία μας;
Κάθε ομάδα θα δουλέψει ξεχωριστά.
-
Οδηγίες - Κατευθύνσεις:
- Υπάρχουν δύο σημεία από τον χάρτη: σημείο εκκίνησης START και το σημείο τέλους END
- Ο σκοπός του παιχνιδιού είναι να υπολογιστεί η απόσταση START - END χωρίς τη βοήθεια μέτρου.
- Μπορείτε να μετακινηθείτε αριστερά ή δεξιά, επάνω ή κάτω, αλλά όχι διαγώνια αποφεύγοντας τα εμπόδια, προκειμένου να πάτε από το σημείο START στο σημείο END
 Κάθε φορά που θα κινείστε προς τα επάνω, κάτω, αριστερά ή δεξιά, πρέπει να σημειώνεται στο σχήμα τη μεταβολή της μετακίνησής σας.
Κάθε φορά που θα κινείστε προς τα επάνω, κάτω, αριστερά ή δεξιά, πρέπει να σημειώνεται στο σχήμα τη μεταβολή της μετακίνησής σας.
π.χ.: εάν μετακινήσετε 2 τετράγωνα προς τα αριστερά (2 τετράγωνα δυτικά), σημειώστε 2, όπως μπορείτε να δείτε στην εικόνα 1
-
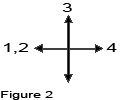 Κατά τον ίδιο τρόπο συνεχίζετε, πάντα σημειώνοντας στο σχήμα, την αλλαγή σε κάθε κίνηση,
Κατά τον ίδιο τρόπο συνεχίζετε, πάντα σημειώνοντας στο σχήμα, την αλλαγή σε κάθε κίνηση,
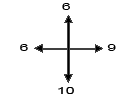
π.χ.: ας πούμε ότι μετά την πρώτη μετακίνηση, θα γίνονται οι ακόλουθες κινήσεις: 3 τετράγωνα πάνω, 4 τετράγωνα προς τα δεξιά και 1 τετράγωνο προς τα αριστερά. Θα πρέπει να σημειωθούν τα αντίστοιχα όπως μπορείτε να δείτε στην εικόνα 2.
- Αφού έχετε φτάσει στο σημείο END, υπολογίστε τους αριθμούς σε κάθε κατεύθυνση,
π.χ. : αν έχετε μετατόπιση προς τα αριστερά 6 και προς τα δεξιά 4, τότε το σύνολο της κίνησης είναι 2 (6 - 4 = 2), προς τα αριστερά - Κάντε το ίδιο για τις άλλες δύο κατευθύνσεις
- Με αυτόν τον τρόπο θα έχετε σε δύο κατευθύνσεις τους αντίστοιχους αριθμούς
- Αυτά είναι τα μήκη των δύο καθέτων πλευρών του ορθογωνίου τριγώνου και η υποτείνουσα είναι η απόσταση που θέλουμε να υπολογίσουμε, η απόσταση ανάμεσα στο σημείο START και στο σημείο END
- Εφαρμόστε το Πυθαγόρειο Θεώρημα και βρείτε την απόσταση START – END
ΠΑΡΑΔΕΙΓΜΑ

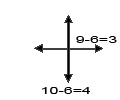
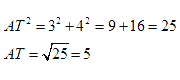
Πρέπει να αποφύγουμε όλα τα εμπόδια ακολουθώντας τα λευκά μονοπάτια. Μπορούμε να διαλέξουμε. Μετράμε τα βήματά μας πάνω, κάτω, αριστερά και δεξιά και υπολογίζουμε. Υπάρχουν πάρα πολλά βήματα και διαφορετικές διαδρομές που μπορούμε να ακολουθήσουμε!
Έτσι ξεκινάμε την περιπέτειά μας για να βοηθήσουμε τους φίλους μας.
Διαδικασία οδηγίες
Θα σας δοθούν 4 διδακτικές ώρες για τη διεξαγωγή της έρευνας σας στο διαδίκτυο και να ολοκληρωθεί αυτό το μέρος του έργου.