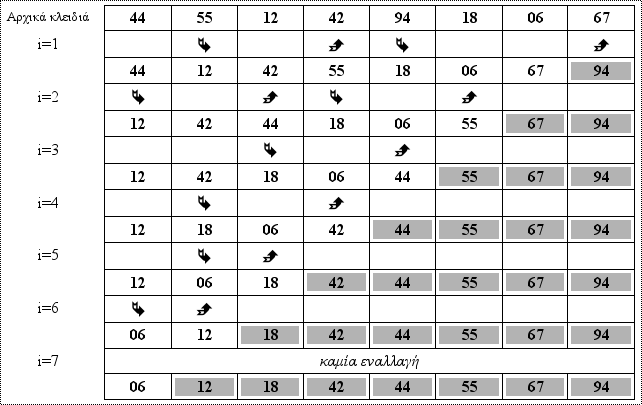
Ο αλγόριθμος ταξινόμησης με ευθεία εναλλαγή στηρίζεται στην αρχή της σύγκρισης και εναλλαγής ζευγαριών γειτονικών στοιχείων μέχρι όλα τα στοιχεία να ταξινομηθούν.

Στο παρακάτω παράδειγμα τα βελάκια δείχνουν πιο στοιχείο μετακινείται προς τα δεξιά και σε ποια θέση καταλήγει. Τα στοιχεία με το γκρι φόντο δείχνουν ποια είναι οριστικά ταξινομημένα.

Βλέπουμε, λοιπόν, ότι σε κάθε βήμα το μεγαλύτερο στοιχείο πηγαίνει στην πιο δεξιά θέση του μη ταξινομημένου πίνακα (στοιχεία με άσπρο φόντο).

Κώδικας

Ορθότητα

Σε κάθε επανάληψη του εσωτερικού βρόχου, ο αλγόριθμος μετακινεί το στοιχείο Α[j] στη θέση Α[j+1] αν το Α[j]>Α[j+1] και τερματίζει όταν φτάσει στο δεξί όριο (n-i) της μη ταξινομημένης ακολουθίας, αφήνοντας την ακολουθία Α[(n-i+1)..n] ταξινομημένη.

Ο εξωτερικός βρόχος τερματίζει όταν το i=n, θα έχει δηλαδή ελεγχθεί όλος ο πίνακας. Έτσι, ο αλγόριθμος ταξινομεί τον πίνακα σε αύξουσα σειρά.

Χρονική Πολυπλοκότητα

Ο εσωτερικός βρόχος for εκτελείται για i=1, n-1 φορές, για i=2, n-2 φορές και για i=n-1, μία φορά. Συνολικά εκτελείται 1+2+...+n-1 φορές, δηλαδή n(n-1)/2.

O εξωτερικός βρόχος εκτελείται n φορές. Ο συνολικός χρόνος είναι:

Ο μεγαλύτερος όρος είναι ο n², άρα ο αλγόριθμος είναι τετραγωνικής πολυπλοκότητας Ο(n²).

Χωρική Πολυπλοκότητα

Ο αλγόριθμος χρησιμοποιεί έναν πίνακα με n στοιχεία και τρεις μεταβλητές, την i, την j, και την temp. Αυτές οι μεταβλητές καταλαμβάνουν από μία θέση μνήμης η κάθε μία. Οπότε, συνολικά η θέσεις μνήμης που χρησιμοποιεί ο αλγόριθμος είναι:

S(n)=n+3

Η χωρική πολυπλοκότητα καθορίζεται από τον μεγαλύτερο όρο της εξίσωσης ο οποίος είναι ο n, δηλαδή, ο αλγόριθμος έχει γραμμική χωρική πολυπλοκότητα O(n).