Προηγούμενη
Άσκηση 1
Επόμενη
Κουτάκια σόδας τοποθετούνται με το πλάι σε ένα κουτί: τέσσερα κόκκινα στη βάση,
τρία πράσινα στη δεύτερη σειρά, τέσσερα πορτοκαλί στην τρίτη σειρά,
και τρία μπλε στην επάνω σειρά. Όταν τα κουτάκια μετακινηθούν, κάποια ενδιαφέροντα πράγματα συμβαίνουν.
Ασχοληθείτε με την παρακάτω εφαρμογή Java και παρατηρήστε προσεκτικά...
Σύρετε με το ποντίκι σας τα σημεία Α και Β, ώστε να μετακινηθούν τα κουτάκια της βάσης (συνεπώς και όλα τα παραπάνω).
Τι συμβαίνει με τα κουτάκια της επάνω γραμμής και γιατί; Για βοήθεια, πατήστε το κουμπάκι "Δείξε την ευθεία ΧΖ".
Πηγή: illuminations.nctm.org
Υπόδειξη
Προφανώς, αυτό που παρατηρούμε είναι ότι τα κέντρα X, Y και Z είναι συνευθειακά. Όμως αυτή η τριάδα συνευθειακών σημείων
δεν είναι η μόνη. Συνολικά υπάρχουν 5 τέτοιες τριάδες. Μπορείτε να τις εντοπίσετε;
Λύση
Όπως αναφέρθηκε στην υπόδειξη, τα σημεία X, Y και Z είναι συνευθειακά. Για να δείτε την απόδειξη, πατήστε με τη σειρά τους επόμενους αριθμούς, που αντιστοιχούν στα βήματα της απόδειξης:
|
<
1
2
3
4
5
6
>
|
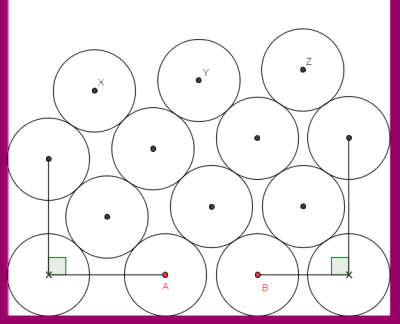
Καταρχήν, ας προσέξουμε τις δύο ορθές γωνίες που σχηματίζονται λόγω των τοιχωμάτων του κουτιού.
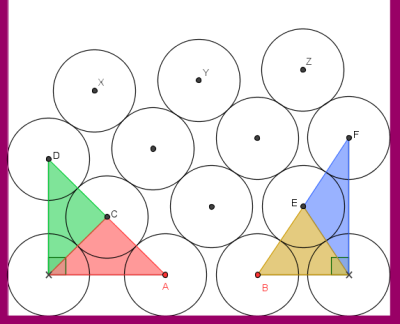
Τα χρωματιστά τρίγωνα είναι ισοσκελή αφού δύο πλευρές τους είναι ίσες με δύο ακτίνες. Ας δούμε όμως τι συμβαίνει με το κόκκινο και πράσινο ισοσκελές τρίγωνο. Οι βάσεις τους σχηματίζουν ορθή γωνία, επομένως, η μία γωνία βάσης του ενός είναι συμπληρωματική με την μία γωνία βάσης του άλλου. Κατά συνέπεια, οι γωνίες των κορυφών τους είναι παραπληρωματικές, που σημαίνει ότι τα σημεία Α, C και D είναι συνευθειακά. Ομοίως και τα B, E και F.
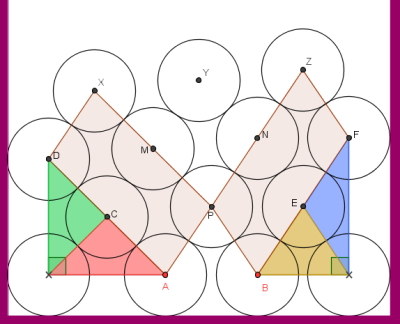
Θεωρώντας τους ίσους ρόμβους XDCM και MYAP, που είναι ενωμένοι πλευρά με πλευρά,
συμπεραίνουμε ότι και τα Χ, Μ, Ρ είναι συνευθειακά. Ομοίως και τα Z, N, P.

Ας εντοπίσουμε και τον πέμπτο ρόμβο στο σχήμα, τον YMPN.
Εξαιτίας του θα δούμε ακόμα δύο παραλληλόγραμμα στην επόμενη διαφάνεια.
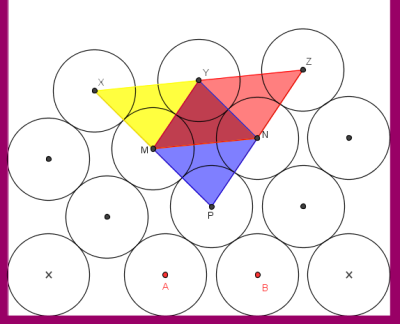
Τα τετράπλευρα XYNM και YZNM είναι παραλληλόγραμμα αφού έχουν XM//=YN, YM//=ZN.

Καθώς XY//MN//YZ, συμπεραίνουμε ότι τα X, Y, Z είναι συνευθειακά.
|
Σχόλιο
Δύο ερωτήματα προς διερεύνηση:
- Αν είχαμε περισσότερους κύκλους στη βάση θα ήταν τα κέντρα των κύκλων της τέταρτης σειράς στην ίδια ευθεία;
- Τι θα συνέβαινε στο σχήμα αν το κουτί είχε μεγαλύτερη βάση;





