5.8 ΦΧΣ 2ης Τάξης
Το Σχ.5.15 δείχνει το κύκλωμα ενός ενεργού ΦΧΣ 2ης τάξης, τύπου
Sallen-Key. Αποδεικνύεται ότι η συνάρτηση μεταφοράς του δίνεται από τη σχέση:


όπου α είναι ένας συντελεστής που η τιμή του βρίσκεται από ειδικό πίνακα - (συντελεστών Butterworth) - και f είναι η συχνότητα αποκοπής
του φίλτρου, η οποία δίνεται από τη σχέση:
Η ενίσχυση Κ δίνεται και πάλι από την Εξ.(5.6.2).
Το φίλτρο αυτό είναι 2ης τάξης, επειδή ο παρονομαστής της συνάρτησης μεταφοράς, όπως βλέπουμε από την Εξ.(5.8.1) είναι πολυώνυμο δεύτερου βαθμού. (Αυτό οφείλεται στο ότι το κυκλωμα έχει δυο στοιχεία αποθήκευσης ενέργειας, δηλ. τους δυο πυκνωτές). Η κλίση του φίλτρου είναι -40 dB/δεκ. ή -12 dB/οκτ, βλ. Εξ.(5.5.1).
Αποδεικνύεται ότι το τυπολόγιο υπολογισμού του φίλτρου αυτού δίνεται από τις σχέσεις:


όπου:
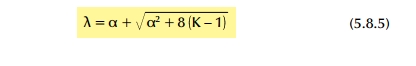
Παράδειγμα 5-3
Θα υπολογίσουμε ΦΧΣ Sallen-Key 2ης τάξης, τύπου Butterworth με ενίσχυση 5 και συχνότητα αποκοπής f1 = 700 Hz.

5.9 ΦΥΣ 2ου βαθμού Sallen-Key
Το Σχ.5.17 δείχνει το κύκλωμα ενός ενεργού ΦΥΣ 2ης τάξης, τύπου Sallen-Key. Αποδεικνύεται ότι η συνάρτηση μεταφοράς του φίλτρου αυτού είναι:
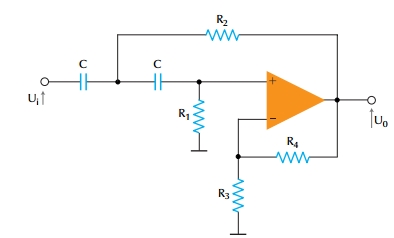
Σχήμα 5.17. ΦΥΣ 2ης τάξης

και
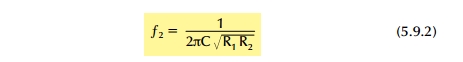
όπου f είναι η συχνότητα αποκοπής του φίλτρου και α ο συντελεστής του φίλτρου.Το τυπολόγιο υπολογισμού του φίλτρου δίνεται απο τις σχέσεις :
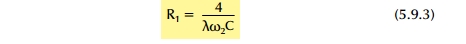

όπου,

Η dc ενίσχυση Κ εξακολουθεί να δίνεται από την Εξ.(5.6.2).
Παράδειγμα 5-4
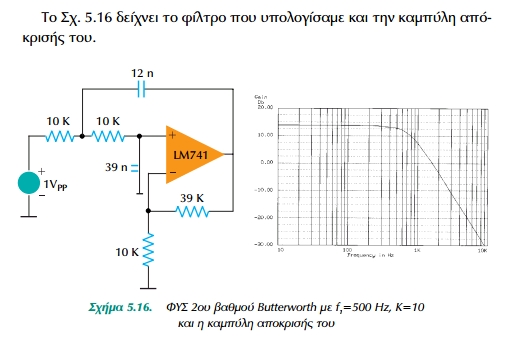
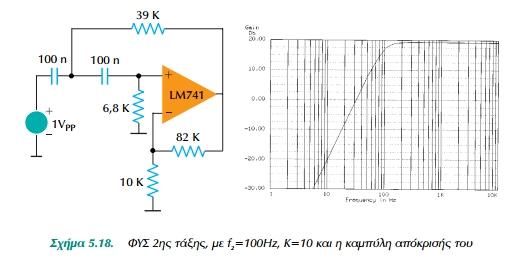
Ζητείται να υπολογίσουμε ΦΥΣ Butterworth με f2 = 100 Hz και Κ=10.

5.10 Φίλτρο στενής ζώνης διέλευσης
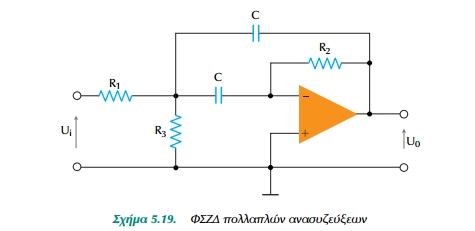
Για να επιτύχουμε στενή ζώνη ο' ένα ΦΣΖΔ, προσφορώτερος τρόπος είναι να εφοδιάσουμε το κύκλωμα με πολλές ανασυζεύξεις. Η τεχνική αυτή λέγεται μέθοδος πολλαπλής ανασύζευξης (ΠΑ) από την έξοδο στην είσοδο του φίλτρου. Ειδικότερα, ανατροφοδοτείται η αναστρέφουσα (-) είσοδος του ΤΕ, Σχ.5.19, πράγμα που δημιουργεί διαφορά φάσης 180° στο σήμα εισόδου και γι' αυτό η συνάρτηση μεταφοράς του φίλτρου αυτού έχει αρνητικό πρόσιμο.
Η συνάρτηση μεταφοράς του φίλτρου δίνεται από τη σχέση:

όπου Κ είναι η ενίσχυση του φίλτρου στην κεντρική συχνότητα fo (συχνότητα συντονισμού) και Q είναι ο συντελεστής ποιότητας ή συντελεστής μεγέθυνσης (ο γνωστός μας από τα κυκλώματα συντονισμού συντελεστής επιλεκτικότητας).
Θα πρέπει να πούμε ότι μ' αυτό το φίλτρο μπορούμε να έχουμε Q μέχρι 10, αν θέλουμε να δουλεύει σωστά.
Η συχνότητα συντονισμού του φίλτρου βρίσκεται από τη σχέση:
: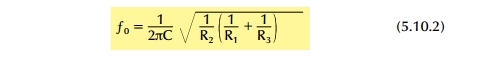
Το τυπολόγιο υπολογισμού του φίλτρου αυτού είναι το πιο κάτω: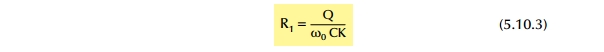

όπου ω0 =2π/f0 .
Η ενίσχυση του φίλτρου υπολογίζεται από τη σχέση:

Παράδειγμα 5-5
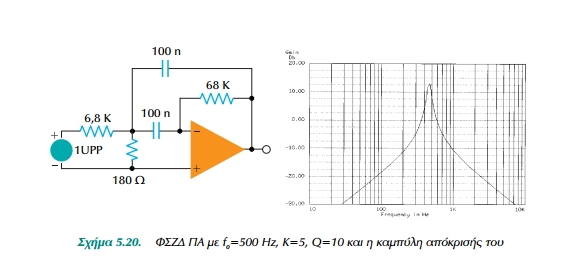
Θα υπολογίσουμε φίλτρο στενής ζώνης διέλευσης ΠΑ με f0=500 Hz,
ενίσχυση 5 και Q = 10.

5.11 Φίλτρο στενής ζώνης αποκοπής
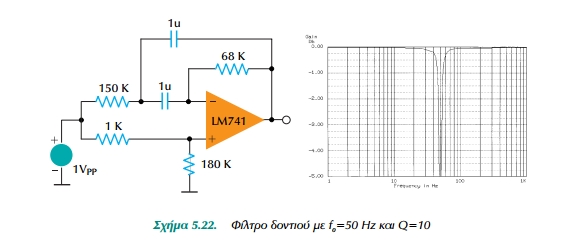
To Σχ.5.21 δείχνει το φίλτρο στενής ζώνης αποκοπής ή φίλτρο δοντιού.
Στη ζώνη αποκοπής εξασθενίζονται οι ανεπιθύμητες συχνότητες. Π.χ. πολλές φορές είναι απαραίτητο να εξασθενήσουμε τα 50 Hz < τα 400 Hz που προέρχονται από το δίκτυο ή στη δεύτερη περίπτωση από έναν κινητήρα.

Η συνάρτηση μεταφορά ενός φίλτρου στενής ζώνης αποκοπής δίνεται από τη σχέση:

όπου Q είναι ο συντελεστής ποιότητας του φίλτρου και f0 η συχνότητα αποκοπής του φίλτρου. Η συχνότητα f0, του φίλτρου δίνεται από τη σχέση:

Οι τύποι υπολογισμού του φίλτρου αποδεκνύεται ότι δίνονται από
τους τύπους:
δεχόμενοι κατάλληλες τιμές των C και R3.
Παράδειγμα 5-6
Θα υπολογίσουμε φίλτρο δοντιού που θα κόβει τη συχνότητα των 50 Hz και θα έχει Q = 10.