6.1 Εισαγωγή - Βασικές αρχές
O ηλεκτρονικός ταλαντωτής είναι ένα κύκλωμα το οποίο δημιουργεί μια έξοδο περιοδικού σήματος χωρίς να εισάγεται σήμα στην είσοδο του. O αρμονικός ταλαντωτής, που συχνά ονομάζεται και γραμμικός ταλαντωτής, είναι υποπερίπτωση των ηλεκτρονικών ταλαντωτών οι οποίοι δημιουργούν στην εξοδό τους σήμα που είναι προσεγγιστικά ημιτονικό.
Οι ταλαντωτές βρίσκουν εφαρμογές σε πολλές περιοχές, μεταξύ των οποίων στα συστήματα ακουστικών συχνοτήτων και στις τηλεπικοινωνίες. Τα συστήματα αυτά χρησιμοποιούν διάφορους ταλαντωτές συμπεριλαμβανομένων των κρυσταλλικών ταλαντωτών και των ταλαντωτών ελεγχόμενους από τάση (VCO). Μολονότι υπάρχει μια ποικιλία ολοκληρωμένων κυκλωμάτων για την παραγωγή περιοδικών σημάτων, οι ταλαντωτές με διακριτά στοιχεία έχουν σημαντικά πλεονεκτήματα απέναντι σε πολλά ολοκληρωμένα κυκλώματα. Έτσι, π.χ. σε πολλές περιπτώσεις οι ταλαντωτές με ολοκληρωμένα κυκλώματα δεν μπορούν να σχεδιαστούν σε υψηλές συχνότητες και μικρούς θορύβους, που είναι απαιτήσεις πολλών τηλεπικοινωνιακών συστημάτων.
Παρομοίως, οι ταλαντωτές που χρησιμοποιούνται στα συστήματα ήχου υψηλής πιστότητας πρέπει να έχουν υψηλή σταθερότητα και χαμηλό θόρυβο και γι' αυτό σχεδιάζονται με διακριτά στοιχεία.
Βασικά, οι αρμονικοί ταλαντωτές χωρίζονται σε δυο μεγάλες κατηγορίες που είναι οι συντονιζόμενοι και οι μη συντονιζόμενοι ταλαντωτές. Οι συντονιζάμενοι αρμονικοί ταλαντωτές αποτελούνται από ένα δικτύωμα συντονισμού LC και ένα ενεργό στοιχείο
(Τρανζίστορ ή Τελεστικό Ενισχυτή), ενώ οι μη συντονιζόμενοι αρμονικοί ταλαντωτές αποτελούνται απο ένα ενεργό στοιχείο και ένα δικτύωμα RC.
Στη συνήθη μορφή του, ο ταλαντωτής είναι ένας ενισχυτής με ανασύζευξη (ανατροφοδότηση) στον οποίο ένα μέρος από την τάση εξόδου του επιστρέφει στην είσοδο του μέσω ενός δικτυώματος ανασύζευξης. Αν το σήμα ανασύζευξης έχει κατάλληλο πλάτος και φάση, το κύκλωμα δημιουργεί από μόνο του (χωρίς σήμα στην είσοδο του) ημιτονική κυματομορφή. Η ισχύς που απαιτείται γι' αυτή την παραγωγή σήματος προσλαμβάνεται από την τάση τροφοδοσίας του κυκλώματος.
6.2 Κριτήρια ταλάντωσης
Το Σχ.6.1β δείχνει το δομικό διάγραμμα που έχει ένας τυπικός αρμονικός ταλαντωτής, θεωρούμενος σα μετεξέλιξη και ειδική περίπτωση ενός ενισχυτή με ανασύζευξη του οποίου το δομικό διάγραμμα εικονίζεται στο Σχ.6.1α.
σημείο

(β)
Όπως παρατηρούμε, το σύστημα αποτελείται από έναν ενισχυτή τάσης (ενεργό στοιχείο), με ενίσχυσης Αν, ένα δικτύωμα ανασύζευξης με υποβιβασμό ή λόγο ανασύζευξης β και ένα σημείο άθροισης. Η ac τάση εξόδου από το σημείο άθροισης συμβολίζεται με Ve και είναι η διαφορά του σήματος εισόδου Vi μείον την τάση (εξόδου) της ανασύζευξης vf (Vi - Vf ). Οι σχέσεις που διέπουν αυτό το δομικό διάγραμμα είναι οι εξής:



Από τις εξισώσεις αυτές αποδεικνύεται η εξής σχέση:

όπου Af είναι η (ολική) ενίσχυση με ανασύζευξη < η ενίσχυση με κλειστό βρόχο, Αν, είναι η ενίσχυση χωρίς ανασύζευξη και β Αν η ενίσχυση του ανοικτού βρόχου.
Από την Εξ.(6.2.4) συνάγεται ότι, αν β Αν =1 τότε | Af | = |νο/ν1|=∞!
Αυτό σημαίνει ότι το σύστημα θα παράγει έξοδο V0 <> 0 χωρίς είσοδο (νi = 0), δηλαδή θα λειτουργεί ως ταλαντωτής με δομικό διάγραμμα αυτό του Σχ.6.1 β.
Συνεπώς, η μιγαδική εξίσωση,

που καλείται συνθήκη Barkhausen, είναι η συνθήκη για να έχουμε εκκίνηση ταλαντώσεων από το σύστημα.
Η εξίσωση αυτή, μετά από κατάλληλη μαθηματική επεξεργασία αποδεικνύεται ισοδύναμη με τις σχέσεις:
οπου, φ η διαφορά φάσης που υπεισάγει το συνολικό κύκλωμα ανοικτού βρόχου (ενισχυτής+δικτύωμα ανασύζευξης). Οι Εξ.(6.2.6) και (6.2.7) δίνουν τις εξής δύο συνθήκες που απαιτούνται για να έχουμε ταλάντωση:
1. Το μέτρο της ενίσχυσης ανοικτού βρόχου β Αν πρέπει να είναι 1.
2. Η ολική μεταβολή φάσης μέσω του ανοικτού βρόχου πρέπει να είναι 00 ή 360°.
Αυτές οι δυο συνθήκες ονομάζονται κριτήρια ταλάντωσης Barkhausen.
Έτσι, αν ο ενισχυτής του Σχ.6.1 δημιουργεί μεταβολή φάσης 1800 τότε, για να έχουμε ταλάντωση το δικτύωμα ανασύζευξης πρέπει να δημιουργεί άλλες 1800 διαφορά φάσης, ώστε η ολική μεταβολή φάσης του συστήματος ανοικτου βρόχου να είναι 3600 (ή 00).
Σημειώστε ότι οι κυματομορφές που δείχνει το Σχ.6.1 είναι ημιτονικές και χρησιμοποιούνται για να δείξουν απλώς τη δράση του κυκλώματος. Στη γενική περίπτωση, οι κυματομορφες που δημιουργούνται απο έναν ταλαντωτή εξαρτώνται από τα στοιχεία του κυκλώματος και επομένως μπορεί να είναι ημιτονικές, τετραγωνικές ή τριγωνικές.
Εξάλλου, η συχνότητα ταλάντωσης καθορίζεται βασικά από τα στοιχεία του δικτυώματος ανασύζευξης.
6.2.1 Εκκίνηση και Συντήρηση των Ταλαντώσεων
Τα κριτήρια Barkhausen, είτε εκφραζονται με τη γενική μιγαδική Εξ.(6.2.5) είτε με τις επιμέρους Εξ.(6.2.6) (μέτρο) και Εξ.(6.2.7) (φαση), αποτελούν μαθηματικές εξισώσεις - συνθήκες κρίσιμων τιμών οι οποίες εξασφαλίζουν απλώς και μόνο την εκκίνηση, (την έναρξη των ταλαντώσεων). Στην πραξη, ταχύτατα, οι συνθήκες αυτές τείνουν να ανατραπούν, είτε γιατί οι τιμές των στοιχείων του κυκλώματος (R, L, C, κ.α.) αλλάζουν, λόγω της διέλευσης του ρεύματος λειτουργίας η της συνεπαγόμενης θέρμανσης του κυκλώματος, είτε γιατί οι παράμετροι του ενεργού στοιχείου (τρανζίστορ, κτλ) μεταβάλλονται για τους ίδιους λόγους. Έτσι, το β και ιδίως το Αν του ενισχυτή παύουν πλέον να ικανοποιούν τη συνθήκη Barkhausen και η ταλάντωση τείνει να αποσβεσθεί, να καταπαύσει. Για να παρακάμψουμε αυτό το πρόβλημα, και να εξασφαλίσουμε συντηρούμενες ταλαντώσεις, αναγκαζόμαστε να δώσουμε στον ενισχυτή του κυκλώματος τιμή ενίσχυσης Αό ελαφρά μεγαλύτερη από όση επιβάλλει η Εξ.(6.2.5). Έτσι, για να έχουμε συντηρούμενες ταλαντώσεις πρέπει να αντιμετωπίσουμε τη συνθήκη Barkhausen όχι σαν ισότητα αλλα σαν ανισότητα της μορφής
οπότε τα κριτήρια Barkhausen, γίνονται
|β Αv|>1 (6.2.9)
και
φ=0° (6.2.10)
Αποδεικνύεται ότι, όταν ικανοποιούνται τα παραπάνω, ο ενισχυτής εξασφαλίζει τη συντήρηση των ταλαντώσεων όχι μόνο με την παροχή της ενίσχυσής του, και της αντίστοιχης ισχύος τροφοδοσίας του, αλλά, και με τη μεσολάβηση ενός φαινομένου που λέγεται περιορισμός του πλάτους. Το φαινόμενο αυτό, που οφείλεται στο ότι η απολαβή τάσης Αό του ενισχυτή ελαττώνεται όσο αυξάνει το πλάτος ταλάντωσης, οδηγεί σε διατήρηση του πλάτους σε σταθερή τιμή.
6.3 Συντονιζόμενοι ταλαντωτές
Οι συντονιζομένοι ταλαντωτές ονομάζονται και ταλαντωτές LC,
γιατί έχουν ως δικτύωμα ανασύζευξης κάποιο κύκλωμα συντονισμού L- C (συχνά συνδυασμένο και με αντιστάσεις R). Οι ταλαντωτές αυτοί χρησιμοποιούνται ιδίως σε εφαρμογές ραδιοσυχνοτήτων, με συχνότητες που κυμαίνονται από αρκετές εκατοντάδες kHz μέχρι αρκετές εκατοντάδες MHz. Οι πιο συνηθισμένοι ταλαντωτές της μορφής αυτής είναι οι ταλαντωτές Colpitis, Clapp και Hartley τους οποίους και θα δούμε αναλυτικότερα παρακάτω.
Η βασική δομή των ταλαντωτών LC απεικονίζεται από το δομικό διάγραμμα του Σχ.6.2. Όπως παρατηρούμε αποτελούνται από έναν ενισχυτή τάσης Αv και από ένα δικτύωμα ανασύζευξης που στη γενική περίπτωση περιλαμβάνει τρία κυκλωματικά στοιχεία, 1, 2, 3 (με L και C) με μεσαία λήψη μεταξύ των 1 και 2. Τα στοιχεία αυτά συγκροτούν ένα γενικό κύκλωμα συντονισμού. Με τη βοήθεια των κριτηρίων Barkhausen αποδεικνύεται, ότι για να έχουμε συντηρούμενες ταλαντώσεις με τους ταλαντωτές αυτούς, πρέπει να ισχύουν οι σχέσεις:
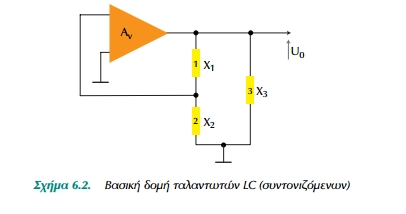
όπου X1 , X2 και X3 είναι φαινόμενες αντιστάσεις, με Xk = ]ω Lk για καθαρές αυτεπαγωγές (πηνία) και Xk = 1 / ]ω Ck για καθαρές χωρητικότητεs(πυκνωτές).
6.3.1 Ταλαντωτής Colpitts
Χαρακτηριστικό γνώρισμα ενός ταλαντωτή Colpitis είναι ότι το συντονιζόμενο κυκλωμά του αποτελείται από δυο πυκνωτές, C1, C2, σε σειρά και το συστημά τους παράλληλο προς το πηνίο L . Οι δυο πυκνωτές δημιουργούν έναν ac διαιρέτη τάσης, και η τάση ανασύζευξης vf είναι αυτή που αναπτύσσεται στα άκρα του C2 (στη μεσαία λήψη μεταξύ των C1 C2 ) και οδηγείται στον ενισχυτή απολαβής Α.
Κατά τα ανωτέρω, αναφερόμενοι και στο Σχ.6.2 για ένα ταλαντωτή
Colpitts θα έχουμε X1 =jωc1 , X2 = jωC2, και X3 = jωL. Από τις σχέσεις αυτές και την Εξ. (6.3.1) προκύπτει η σχέση

όπου, Ct η ισοδυναμη χωρητικότητα σύνδεσης των C1 και C2 σε σειρά, δηλ.

Παρόμοια, από την Εξ.(6.3.2) βρίσκουμε, ότι για να έχουμε συντηρούμενες ταλαντώσεις πρέπει να ισχύει

Το Σχ.6.3 εικονίζει τον ταλαντωτή Colpitts με τρανζίστορ (BJT) σε συνδεσμολογία CB. Η θετική ανασύζευξη από την ακραία έως τη μεσαία λήψη μεταξυ των C1, C2, οδηγείται στην είσοδο του τρανζίστορ. Στον εκπομπό παρεμβάλλεται η αντίσταση Re η οποία μαζί με τις R και R2, δημιουργουν την πόλωση του τρανζίστορ. Ταυτόχρονα, όμως, ασκεί και αρνητική ανασυζευξη στη λειτουργία του, για να βελτιώσει την ημιτονική κυματομορφή που παράγεται από τον ταλαντωτή. Τέλος, η RC είναι η κλασσική αντίσταση συλλέκτη του τρανζίστορ.

Αν λάβουμε υπόψη μας την έκφραση της απολαβής Λό του ενισχυτή σε
συνάρτηση των υβριδικών παραμέτρων του τρανζίστορ, η Εξ.(6.3.5) γίνεται:

όπου

Παράδειγμα 6-1
Ο πιο πάνω ταλαντωτής Colpitis με BJT υλοποιείται με τις εξής τιμές εξαρτημάτων: L=100μΗ, C1 = 1 nF, C2 = 100 pF, Rc=680 Ω, R1=18 kΩ, R2 = 5.6 kΩ, Re=47 Ω. Εξάλλου, το τρανζίστορ έχει hie=1 kΩ και hfe=199. Να βρεθεί η συχνότητα ταλαντώσεών του και να εξεταστεί αν συντηρούνται οι ταλαντώσεις αυτές.
Επομένως ικανοποιείται η ανισότητα της Εξ.(6.3.6), άρα έχουμε
συντήρηση ταλαντώσεων.
Το κύκλωμα του Σχ.6.4 εικονίζει τον ταλαντωτή Colpitts με ΤΕ. O ΤΕ
δίνει την απαραίτητη ενίσχυση για να έχουμε συντήρηση των ταλαντώσεων. Η συχνότητα ταλάντωσης εξακολουθεί να δίνεται από την Εξ.(6.3.3).
Επίσης, για να έχουμε συντήρηση ταλαντώσεων θα πρέπει και πάλι να ισχύει η ανισοτική Εξ.(6.3.5)
Τέλος, όπως φαίνεται από το σχήμα, ο συντελεστής ανασυζευξης
β (X2 / (X1 + X2)) δίνεται από τη σχέση:
(Εδώ έχει ληφθεί υπόψη, ότι η αντίσταση εισόδου του ΤΕ είναι πολυ
μεγάλη).

Παράδειγμα 6-2
Θα υπολογίσουμε ταλαντωτή Colpitts με ΤΕ, συχνότητας 50 kHz, χρησιμοποιώντας τον 741 (Ri = 2 ΜΩ, R0 = 70 Ω).

Για την R1 δεχόμαστε μια τιμή R1 > XC1 ώστε το δικτύωμα να μη φορτώνει τον ενισχυτή.
Στην πράξη παίρνουμε,

οπου,

Η αντίσταση R2 στην πράξη είναι συνήθως ένα ποτενσιόμετρο που το ρυθμίζουμε γυρω από την παραπάνω τιμή ώστε να έχουμε καλό ημιτονικό σήμα στην έξοδο του ταλαντωτή.









