7.6 Αποδιαμόρφωση ή διευκρίνιση συχνότητας
7.6.1 Διευκρινιστής με φίλτρο
Αποδιαμόρφωση συχνότητας ή διευκρίνηση συχνότητας, όπως συνήθως αποκαλείται, είναι η διαδικασία εξαγωγής της πληροφορίας από φέρον σήμα διαμορφωμένο κατά συχνότητα.
Στη διαμόρφωση FM, ως γνωστόν, η πληροφορία επηρεάζει αποκλειστικά τη συχνότητα του φέροντος, με βάση τη γραμμική σχέση:
f(t) = fo + Δf(t) = fο + k.s(t) .
Αυτό πραγματοποιείται με ταλαντωτή VCO.
Ο διευκρινιστής συχνότητας αντίστροφα μετατρέπει τις μεταβολές συχνότητας του φέροντος σε μεταβολές τάσης και πρέπει να είναι γραμμικός (σχήμα 7.6.2(α)) Η κλίση της χαρακτηριστικής του
k΄= ΔV/Δf δίνεται σε V/Hz. (21)
Το πλάτος του σήματος στη διαμόρφωση FM δεν επηρεάζεται από την πληροφορία και παραμένει σταθερό. Αυτή η παρατήρηση δίνει τη δυνατότητα να προηγηθεί του σταδίου αποδιαμόρφωσης του σήματος ένας συμμετρικός περιοριστής (ψαλιδιστής) (σχήμα 7.6.1), που ψαλιδίζοντας τις κορυφές του φέροντος το απαλλάσει από παρασιτικές κυματώσεις και παρασιτικές αλλοιώσεις, που τυχόν προήλθαν από θόρυβο, βιομηχανικά παράσιτα κλπ. Αυτή η διαδικασία συνεισφέρει στην καλύτερη ποιότητα του δέκτη FM απαλλάσσοντας τον αποδιαμορφωτή από τις παρασιτικές διακυμάνσεις του σήματος και αυξάνει τελικά το λόγο σήματος προς θόρυβο στην έξοδο. Στην έξοδο του ψαλιδιστή το μεσοπερατό φίλτρο L-C αποκαθιστά την ημιτονική φυσιογνωμία του ψαλιδισμένου φέροντος.
Σχήμα 7.6.1: Συμμετρικός περιοριστής και η λειτουργία του.
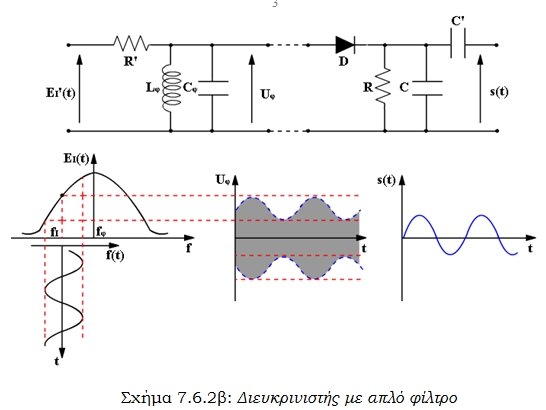
Ως απλός διευκρινιστής συχνότητας αξιοποιείται ένα απλό επιλεκτικό φίλτρο, σαν αυτό του σχήματος 7.6.2. Η απόκριση του φίλτρου επιλέγεται έτσι, ώστε η κεντρική συχνότητα του φέροντος να βρίσκεται περίπου στο μέσο του ανοδικού ή καθοδικού τμήματος της χαρακτηριστικής του.
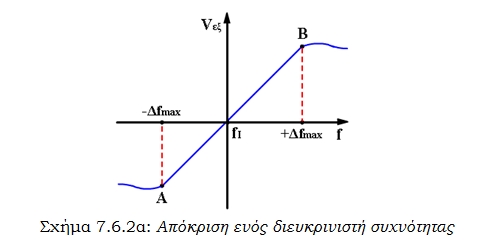
Σχήμα 7.6.2α: Απόκριση ενός διευκρινιστή συχνότητας
Σχήμα 7.6.2β: Διευκρινιστής με απλό φίλτρο
Είναι προφανές ότι με τέτοια διάταξη το φέρον σήμα, του οποίου η συχνότητα παρουσιάζει μεταβολές γύρω από την κεντρική του συχνότητα, μετά την διέλευση από το φίλτρο είναι διαμορφωμένο και κατά πλάτος, όπως χαρακτηριστικά απεικονίζεται στο σχήμα. Στη συνέχεια προσφέρεται ένας απλός φωρατής αναπτύγματος (πλάτους) D – R – C, που μελετήθηκε σε προηγούμενη παράγραφο για να έχουμε αποδιαμόρφωση .
Η σχετικά απλή διάταξη του σχήματος με ένα φίλτρο παρουσιάζει ένα βασικό μειονέκτημα. Η χαρακτηριστική απόκριση του φίλτρου δεν είναι γραμμική, με αποτέλεσμα όταν οι μεταβολές συχνότητας είναι μεγάλες, να εμφανίζονται στην έξοδο παραμορφώσεις του σήματος. Έτσι, η χρήση της διάταξης περιορίζεται σε περιπτώσεις διαμόρφωσης FM με μικρή απόκλιση συχνότητας Δfmax, όπου το τμήμα ΑΒ της χαρακτηριστικής μπορεί να θεωρηθεί γραμμικό (σχήμα 7.6.2β). Το μειονέκτημα αυτό διορθώνεται από συνθετότερες διατάξεις, όπως αυτή του σχήματος 7.6.3 όπου αξιοποιούνται δύο φίλτρα και δύο φωρατές αναπτύγματος.
Σχήμα 7.6.3: (α)Διευκρινιστής Fooster-Seeley
(β) Χαρακτηριστική απόκρισης
Τα δύο φίλτρα που είναι δομημένα με τον ίδιο πυκνωτή C (φίλτρο L1-C και L2-C) λειτουργούν με διαφορά φάσης π, έτσι όπως ο συνδυασμός τους απεικονίζεται στη γραφική παράσταση του σχήματος 7.6.3 (α) και η μη γραμμικότητα του ενός αντισταθμίζεται από τη μη γραμμικότητα του άλλου. Η χαρακτηριστική του αποδιαμορφωτή εκτείνεται σε ευρύτερη, όπως φαίνεται στο σχήμα, περιοχή. Το ωφέλιμο σήμα είναι η διαφορά των σημάτων V1 και V2 που προκύπτουν στις εξόδους των δύο φωρατών αναπτύγματος.
Στο σχήμα 7.6.4 απεικονίζεται διανυσματικά η λειτουργία του αποδιαμορφωτή, που είναι γνωστός με το όνομα διευκρινιστής Fooster – Seeley. Ο συνδυασμός των φίλτρων L1-L2-C αποτελεί συντονισμένο κύκλωμα στην κεντρική συχνότητα του φέροντος (fo).
Σχήμα 7.6.4: Διανυσματική εξήγηση της λειτουργίας του FoosterSeeley
Γι’ αυτή τη συχνότητα τα διανύσματα τάσης και ρεύματος είναι συμφασικά και οι τάσεις εξόδου αντιπροσωπεύονται από διανύσματα κάθετα στο ρεύμα και αντίθετα μεταξύ τους. Αποτέλεσμα, οι τάσεις V1 και V2 είναι ίσες και τελικά το σήμα εξόδου s(t) = V1 – V2 = 0. Σε οποιαδήποτε άλλη περίπτωση τα διανύσματα ρεύματος και τάσης παρουσιάζουν διαφορά φάσης
απ΄ όπου προκύπτουν τα διανυσματικά διαγράμματα 7.6.4 (β) και (γ). Οι μεταβολές συχνότητας απεικονίζονται στη διαφορά των τάσεων V1 και V2. Η τάση στην έξοδο είναι ανάλογη προς τις μεταβολές της συχνότητας.
7.6.2 Άλλα κυκλώματα αποδιαμόρφωσης
Μια παραλλαγή του κυκλώματος σύγχρονης φώρασης, που μελετήθηκε στις αποδιαμορφώσεις πλάτους, μπορεί να αξιοποιηθεί για αποδιαμόρφωση σημάτων διαμορφωμένων κατά συχνότητα. Στην περίπτωση του σχήματος 7.6.5 το φέρον FM πολλαπλασιάζεται με τον εαυτό του, αφού υποστεί ολίσθηση φάσης (-π/2). Η ολίσθηση φάσης (-π/2) αντιστοιχεί στην κεντρική συχνότητα φέροντος.
Σχήμα 7.6.5: Αποδιαμόρφωση FM με παραλλαγή του σύγχρονου φωρατή
Καθώς η συχνότητα μεταβάλλεται, η στιγμιαία ολίσθηση φάσης μεταβάλλεται επίσης και είναι:
-π/2 + Δφ (σημειώνεται στο σχήμα).
Αν υποθέσουμε ότι η διαφοροποίηση της φάσης Δφ είναι ανάλογη προς τις μεταβολές συχνότητας και υπακούει στη σχέση
Δφ = λ[f(t) – fo] (λ = rad/Hz) , (22)
τότε Δφ = λ. k. s(t).
Αν θέσουμε Ε(t) = Eocos[Φ(t)], τότε E΄(t) = -Eosin[Φ(t) – Δφ].
Εκτελώντας τις πράξεις βρίσκουμε στην έξοδο:
Vεξ = sinΔφ ≈ Δφ = λ. k. s(t). (23)
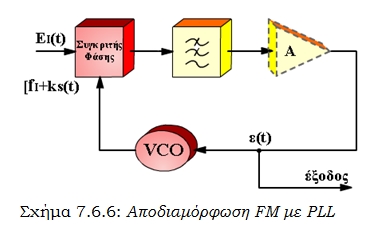
Ο βρόχος φάσης PLL, χρησιμοποιείται ευρύτατα για αποδιαμόρφωση FM. Το γενικό διάγραμμα του αποδιαμορφωτή φαίνεται στο σχήμα 7.6.6. Η συχνότητα του σήματος εισόδου συγκρίνεται με τη συχνότητα του VCO, που είναι υπολογισμένος με κεντρική συχνότητα ίδια με του φέροντος. Η τάση ελέγχου του VCO, που προσπαθεί να τον συγχρονίσει στη συχνότητα του σήματος εισόδου αντιπροσωπεύει τις μεταβολές της συχνότητας του, δηλαδή το ωφέλιμο σήμα s(t).
Σχήμα 7.6.6: Αποδιαμόρφωση FM με PLL
Μετά την αποδιαμόρφωση το ωφέλιμο σήμα s(t) θα υποστεί αποέμφαση, δηλαδή την αντίστροφη διαδικασία της έμφασης, στην οποία υποβλήθηκε στον πομπό. Ειδικό χαμηλοδιαβατό φίλτρο (σχήμα 7.6.7) αποκαθιστά τη φασματική φυσιογνωμία του σήματος, πριν την τελική του ενίσχυση από τους ενισχυτές χαμηλών συχνοτήτων.
Σχήμα 7.6.7: Φίλτρο αποέμφασης στην FM
Σήμερα για τα σήματα AM και FM υπάρχουν ολοκληρωμένα κυκλώματα που ενσωματώνουν τα στάδια ενίσχυσης ενδιάμεσης συχνότητας και αποδιαμόρφωσης.
7.7 Θόρυβος και ευαισθησία στο δέκτη
Ένα από τα βασικότερα χαρακτηριστικά του δέκτη είναι η ευαισθησία του. Ορίζεται ως η ελάχιστη ένταση του σήματος στην είσοδο του δέκτη, ώστε στην έξοδο ο λόγος ισχύος του ωφέλιμου σήματος (συμβολίζεται S) προς την ισχύ του θορύβου (συμβολίζεται N), δηλαδή ο λόγος S/N να έχει δεδομένη τιμή. Το πρόβλημα που τίθεται είναι ο προσδιορισμός της μαθηματικής σχέσης που συνδέει την ένταση του φέροντος σήματος στην είσοδο του δέκτη με το λόγο S/N στην έξοδο.
Η μοντελοποίηση του θορύβου είναι από τα δυσκολότερα κεφάλαια της ηλεκτρονικής και η αναλυτική μελέτη του προβλήματος ξεφεύγει από το πλαίσιο αυτού του βιβλίου. Περιοριζόμαστε σε γενικά ποσοτικά συμπεράσματα, από όπου όμως βγαίνουν σημαντικές παρατηρήσεις.
Για να απλοποιηθεί η μελέτη της συμπεριφοράς του δέκτη ως προς τον θόρυβο, θεωρούμε ότι ο δέκτης αποτελείται ουσιαστικά από δύο τμήματα, όπως φαίνεται στο σχήμα 7.7.1. Το ένα τμήμα περιλαμβάνει όλα τα στάδια, πριν την αποδιαμόρφωση (στάδια RF και IF), ενώ το δεύτερο περιλαμβάνει την αποδιαμόρφωση και το τμήμα ενίσχυσης χαμηλών συχνοτήτων.

Σχήμα 7.7.1: Μελέτη του θορύβου στο δέκτη
Ορίζουμε:
- (S/N) : το λόγο ισχύος του ωφέλιμου βασικού σήματος προς τον θόρυβο στην έξοδο του δέκτη.
- (S΄/Ν΄) : το λόγο ισχύος σήματος προς θόρυβο στην είσοδο του αποδιαμορφωτή. Το μέγεθος S΄αναφέρεται στο σήμα που προέκυψε από τη διαδικασία ενίσχυσης και ετεροδύνωσης, ενώ ο θόρυβος Ν΄ είναι αθροιστικά ο θόρυβος εισόδου επιβαρυμένος από το θερμοδυναμικό θόρυβο των κυκλωμάτων του δέκτη.
- Si / Ni) το λόγο ισχύος του φέροντος σήματος πρός το θόρυβο στην έξοδο του δέκτη.
Στην είσοδο του δέκτη ο θόρυβος θεωρείται με σταθερή πυκνότητα ισχύος σε όλο το φάσμα των συχνοτήτων. Ονομάζεται λευκός θόρυβος και η ισχύς του δίνεται από τη σχέση:
Νi = kTB , (24)
όπου k η σταθερά Boltzman (k=1,38.10-23J.K-1), Tη θερμοκρασία περιβάλλοντος σε βαθμούς Kelvin (Κ) και Β (Ηz) το εύρος ζώνης του φέροντος (εύρος ζώνης του σταδίου ενδιάμεσων συχνοτήτων).
Η συμπεριφορά του δέκτη στο πρώτο τμήμα του σχήματος 7.7.1 περιγράφεται από το συντελεστή θορύβου GR του δέκτη και είτε δίνεται στα τεχνικά χαρακτηριστικά του δέκτη είτε μετριέται πειραματικά. Ορίζεται από τη σχέση:
(Si/Ni) = GR .(S΄/N΄) (25)
Η σχέση που συνδέει τους λόγους (S΄/N΄) και (S/N) στην είσοδο και στην έξοδο αντίστοιχα του αποδιαμορφωτή εξαρτάται από τον τύπο της διαμόρφωσης. Υποθέτοντας ότι ισχύει S΄>> N΄, δηλαδή ότι το σήμα είναι ισχυρότερο από το θόρυβο (τουλάχιστον δέκα φορές), αποδεικνύεται ότι:
- Στη διαμόρφωση πλάτους:
(S/N) = m2 . (S΄/N΄) , (26)
όπου m το πoσοστό διαμόρφωσης.
Αν m=1, τότε
(S/N) = (S΄/N΄).
- Στη διαμόρφωση συχνότητας:
(S/N) = [3m2(m+1)](S΄/N΄) , (27)
όπου m ο δείκτης διαμόρφωσης.
Αν m>>1, τότε:
(S/N) = [3m3 .(S΄/N΄).
Συνδυάζοντας τις σχέσεις (26) και (27) με τις σχέσεις (24) και (25), έχουμε:
Για την ΑΜ:
Si = (1/m2)kTBGR(S/N) = 2kTFmax . GR . (1/m2) (S/N) (28)
(διότι Β = 2Fmax)
Αν m =1 (100%), τότε: Si = 2kTFmax.GR . (S/N) (29)
Για την FM:
Si = kTBGR [1/3m2(m+1)](S/N) =
= 2kTFmax . GR .(1/3m2).(S/N) (30)
(διότι Β = 2Fmax(m+1) )
Οι τελευταίες σχέσεις συνδέουν την ισχύ που πρέπει να έχει το φέρον σήμα στην είσοδο του δέκτη με τον επιθυμητό λόγο σήματος πρός θόρυβο στην έξοδο.
Αν θέλουμε οι προηγούμενες σχέσεις να αναφέρονται όχι στην ισχύ, αλλά στην ενεργό τιμή του σήματος εισόδου (θεωρώντας την κεραία ως γεννήτρια), πρέπει να ληφθεί υπόψη ότι :
Si = E2 /4Ri , όπου Ri η ισοδύναμη αντίσταση εισόδου του δέκτη, που συνήθως λαμβάνεται 50 Ω (προσαρμογή με την κεραία).
Εφαρμογή: Σε δέκτη ΑΜ δίνονται FR = 6 , αντίσταση εισόδου R = 50 Ω, Fmax = 3 kHz και ποσοστό διαμόρφωσης 60%. Ο επιθυμητός λόγος σήματος προς θόρυβο στην έξοδο είναι S/N = 400 (ή 26 dΒ), και η θερμοκρασία περιβάλλοντος 23 Co ( ή 273 +23 =296 Κ). Να υπολογιστεί η ενεργός τιμή του σήματος στην είσοδο του δέκτη.
Λύση: Από τις προηγούμενες σχέσεις εύκολα απορρέει ότι:
Ε = (1/m)√8kTRGR.Fmax (S/N).
Αντικαθιστώντας, βρίσκουμε Ε = 5,5 μV.
7.8 Σύγκριση ΑΜ και FM ως προς το θόρυβο
Συγκρίνοντας τις σχέσεις (29) και (30), εύκολα διαπιστώνουμε ότι για το ίδιο σήμα Si στην είσοδο του δέκτη ισχύει:
(S/N)FM = 3m2 .(S/N)AM . (31)
Αν m>1, τότε: (S/N)FM > (S/N)AM
Η διαμόρφωση FM παρουσιάζει μεγαλύτερη αντοχή στο θόρυβο. Στην περίπτωση της ραδιοφωνίας FM, m ≥ 5, άρα:
(S/N)FM = 3 . 52 . (S/N)AM ή (S/N)FM = 75 . (S/N)AM (32)
ή εκφραζόμενοι σε dB:
(S/N)FM = (S/N)AM + 18,8 dB.
Το πλεονέκτημα της FΜ είναι σημαντικό. Τα συμπεράσματα αυτά, που ισχύουν με την προυπόθεση ότι το σήμα στην είσοδο του αποδιαμορφωτή είναι μεγαλύτερο από το θόρυβο (S΄>> N΄),
απεικονίζονται στη γραφική παράσταση του σχήματος 7.8.1.
Σχήμα 7.8.1: Σύγκριση AM και FM ως προς το θόρυβο
Για μικρές τιμές του λόγου S΄/ N΄ (<10), το πλεονέκτημα της FM παύει να ισχύει. Το φαινόμενο αυτό είναι γνωστό στους τηλεπικοινωνιακούς ως ‘φαινόμενο κατωφλίου’.