9.2 Ψηφιακές διαμορφώσεις αναλογικού φέροντος
Στις ψηφιακές διαμορφώσεις αναλογικού φέροντος το φέρον είναι ημιτονικό σήμα M(t) και το σήμα διαμόρφωσης είναι ψηφιακή πληροφορία δυαδική (δύο καταστάσεων ‘0’ ,’1’ ) ή Κ-αδική (Κ διαφορετικών καταστάσεων, που αντιπροσωπεύονται από ομάδες – κώδικες των log2 Κ bits). Κάποια παράμετρος (το πλάτος, η συχνότητα ή η φάση) του διαμορφωμένου φέροντος Ε(t) μεταβάλλεται στο ρυθμό της πληροφορίας.
9.2.1 Διαμόρφωση ASK ή OOK
Πρόκειται για διαμόρφωση πλάτους (AmplitudeShiftKeying).
Οι Κ διακριτές καταστάσεις της πληροφορίας αντιπροσωπεύονται από διαφορετικές τιμές πλάτους του φέροντος σήματος. Στην περίπτωση που Κ=2 (δυαδικές καταστάσεις) έχουμε την διαμόρφωση ΟΟΚ (On-OffKeying), που φαίνεται στη γραφική παράσταση του σχήματος 9.2.1.

Σχήμα 9.2.1: Διαμόρφωση OOK
Το διαμορφωμένο σήμα Ε(t) δίνεται από την έκφραση:
Ε(t) = a(t). cos(ωοt), (10)
με a(t) = 0 ή 1.
Η σχέση θυμίζει την πολλαπλασιαστική διαμόρφωση DSB, που γνωρίσαμε στις αναλογικές διαμορφώσεις. Το φάσμα περιλαμβάνει θεωρητικά δύο πλάγιες ζώνες άπειρου εύρους (ένα καθαρό δυαδικό σήμα έχει άπειρο φασματικό εύρος) και φασματική συνιστώσα του φέροντος που οφείλεται στη συνεχή συνιστώσα του διαμορφώνοντος σήματος (σχήμα 9.9.2α).
Σχήμα 9.2.2: (α) Φάσμα σήματοςΟΟΚ. (β) Γενικό διάγραμμα διαμορφωτή ΟΟΚ
Στην πράξη, αν Rs (= R) ο επιθυμητός ρυθμός εναλλαγής της πληροφορίας σε bits/sec, Β η φασματική ζώνη του ψηφιακού σήματος, τότε: Β = 0,8 R
Το εύρος του φάσματος μετά τη διαμόρφωση είναι :
Βολ = 2Β = 2 . 0,8R = 1,6R (11)
Το γενικό διάγραμμα διαμορφωτή ΟΟΚ φαίνεται στο σχήμα 9.2.2β.
9.2.2 Διαμόρφωση FSK δύο καταστάσεων
Πρόκειται για διαμόρφωση συχνότητας (FrequencyShiftKeying) όπου η συχνότητα του φέροντος για τις δύο δυαδικές καταστάσεις ‘0’ και ‘1’ παίρνει δύο διακριτές διαφορετικές τιμές:
Για στάθμη ‘0’ : f = fo – Δf
Για στάθμη ‘1’ : f = fo + Δf

Σχήμα 9.2.3: Διαμόρφωση FSK
Η χρονική εικόνα του σήματος φαίνεται στο σχήμα 9.2.3 και η μαθηματική έκφραση δίνεται από τη σχέση:
E(t) = Eocos{ 2πfot + 2π[a(t)Δf]t } , (12)
όπου a(t) = 1 ή –1 .
Η FSK αντιστοιχεί στη διαμόρφωση FM.
Ο γενικός τελεστής διαμόρφωσης FSK φαίνεται στο σχήμα 9.2.4α. Το σήμα FSK προκύπτει από το συνδυασμό δύο ανεξάρτητων ταλαντωτών με συχνότητες fo – Δf και fo + Δf διαμορφωμένων με OOK. Ο μηχανισμός δημιουργίας του FSK σήματος φαίνεται στο σχήμα 9.2.4β και δικαιολογεί την ύπαρξη ενδεχομένως ασυνεχειών στη φάση του σήματος κατά την εναλλαγή των καταστάσεων (σχήμα 9.2.3).

Σχήμα 9.2.4: (α) Γενικό διάγραμμα διαμορφωτή FSK. (β) Μηχανισμός δημιουργίας του σήματος FSK
Στην πράξη τις περισσότερες φορές η διαμόρφωση FSK πραγματοποιείται με την αξιοποίηση ενός VCO, που ελέγχεται από το σήμα a(t), όπως φαίνεται στο σχήμα 9.2.5. Στην περίπτωση αυτή, καθώς δε δικαιολογούνται ασυνέχειες των φάσεων του σήματος, μιλούμε για διαμόρφωση CPFSK(ContinuousPhaseFreqyencyShiftKeying).

Σχήμα 9.2.5: Διαμορφωτής με VCO (CPFSK)
Από τον τρόπο σύνθεσης του σήματος FSK (σχήμα 9.2.4) μπορεί να εκτιμηθεί εύκολα το φάσμα και το εύρος της φασματικής ζώνης. Αυτό απεικονίζεται στο σχήμα 9.2.6, απ’ όπου φαίνεται ότι μετά τη διαμόρφωση έχουμε:
Βολ = 2Β + 2Δf (13)
Β = 0,8Rs (Rs = Rσε bits/sec)
Η σχέση αυτή θυμίζει τη σχέση του Carson στις αναλογικές διαμορφώσεις.

Σχήμα 9.2.6: Το φάσμα στη διαμόρφωση FSK
Στην περίπτωση της CPFSK ο ακριβής υπολογισμός του φάσματος είναι δυσκολότερος. Το εύρος φάσματος εξαρτάται από τις παραμέτρους Δf και R, ενώ η ακριβής φασματική εικόνα εξαρτάται από το λόγο Δf/R.
9.2.3 Διαμόρφωση PSK
Στη διαμόρφωση PSK(PhaseShiftKeying) οι Κ διακριτές καταστάσεις της πληροφορίας επηρεάζουν την αρχική φάση του φέροντος σήματος.
Η μαθηματική έκφραση του διαμορφωμένου φέροντος δίνεται από τη σχέση:
Ε(t) = Eocos[ωοt + φο + a(t). 2π/Κ], (14)
όπου a(t) є { 0,1,2, …K-1} και φο η αρχική φάση του σήματος
Διαμόρφωση BPSK: Στην περίπτωση που Κ =2, (η διαμόρφωση αναφέρεται ως BPSK(BinaryPhaseShiftKeying) και a(t) = 0 ή 1. Άρα:
Ε(t) = Eocos[ωοt + a(t)π ] = ± Εοcos(ωοt) (15)
Η BPSK μπορεί να θεωρηθεί ως διαμόρφωση DSBsc (κεφάλαιο 3) με σήμα διαμόρφωσης α = ±1. Ο γενικός τελεστής διαμόρφωσης BPSK δίνεται στο σχήμα 9.2.7α και η χρονική εικόνα του σήματος αποδίδεται στο σχήμα 9.2.7β.
(β)
Σχήμα 9.2.7: (α) Διάγραμμα διαμορφωτή BPSK. (β) Εικόνα του σήματος BPSK
Η φασματική εικόνα είναι η ίδια με την περίπτωση της ΟΟΚ, με τη διαφορά ότι στην περίπτωση της BPSK δεν υπάρχει φασματική συνιστώσα του φέροντος (στη συχνότητα fo).
Διαμόρφωση QPSK: Στην περίπτωση που Κ = 4, η διαμόρφωση PSK αναφέρεται ως QPSK( QuadraturePhaseShiftKeying).
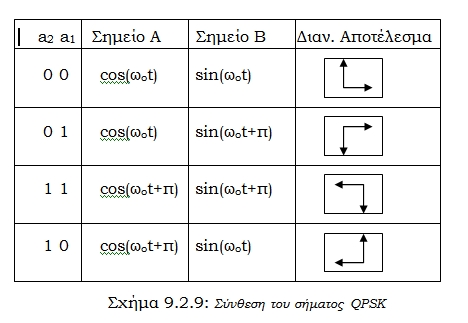
Πρόκειται για διαμόρφωση φάσης τεσσάρων διακριτών καταστάσεων που αντιστοιχούν (όπως φαίνεται στον πίνακα του σχήματος 9.2.9) σε πληροφορία που κωδικοποιείται από ένα ζευγάρι δυαδικών στοιχείων: ‘00’, ‘01’, ‘10’, ‘11’.
Στο σχήμα 9.2.8 δίνεται το γενικό διάγραμμα ενός διαμορφωτή QPSK, που αποτελείται από δύο διαμορφωτές BPSK οι οποίοι εργάζονται με ορθογώνια φέροντα (παρουσιάζουν διαφορά φάσης π/2).
Σχήμα 9.2.8: Γενικό διάγραμμα διαμορφωτή QPSK.
Τα σήματα των δύο διαμορφωτών αθροίζονται στην έξοδο. Το διανυσματικό αποτέλεσμα (διαμόρφωση QPSK) εμφανίζεται στο σχήμα 9.2.9.
Σχήμα 9.2.9: Σύνθεση του σήματος QPSK
Η μαθηματική έκφραση του διαμορφωμένου σήματος που προκύπτει είναι:
E(t) = Eocos(ωοt + π/4 + aπ/2) , (16)
όπου a = 0,1,2,3.
Η αποδιαμόρφωση των σημάτων OOK, FSK και PSK στο δέκτη γίνεται με τη χρήση σύμφωνου (σύγχρονου ) αποδιαμορφωτή.
Στην έξοδο του αποδιαμορφωτή συνήθως οι παλμοί (η ψηφιακή πληροφορία) εμφανίζονται παραμορφωμένοι, λόγω του περιορισμού που υπέστη το φάσμα τους στο τηλεπικοινωνιακό κανάλι. Γι’ αυτό πάντοτε μετά την αποδιαμόρφωση ακολουθεί στάδιο επαναμορφοποίησης των παλμών (σχήμα 9.2.10).
Σχήμα 9.2.10: Μορφοποίηση των παλμών μετά την αποδιαμόρφωση
Υπάρχουν πολλά είδη ψηφιακών διαμορφώσεων ημιτονικού φέροντος που δε θα μελετηθούν εδώ. Η σύγκριση των διαφόρων μεθοδολογιών δεν είναι πάντοτε εύκολη υπόθεση. Το ζητούμενο στις ψηφιακές τηλεπικοινωνίες είναι να επιτευχθεί όσο το δυνατόν μεγαλύτερος ρυθμός πληροφορίας ανά μονάδα χρόνου (μεγάλος όγκος πληροφορίας), με το μικρότερο δυνατό εύρος φάσματος και τη μικρότερη ισχύ φέροντος σήματος. Για τούτο βασική παράμετρος που χαρακτηρίζει τις ψηφιακές διαμορφώσεις και δίνει ένα μέτρο σύγκρισης μεταξύ τους είναι η φασματική αποτελεσματικότητα η . Ορίζεται από τη σχέση:
η = R/Bολ , (17)
όπου R ο ρυθμός μετάδοσης (το bitrate σε bits/sec) και Βολ η ολική φασματική ζώνη στο τηλεπικοινωνιακό κανάλι.
Το μέγεθος η εξαρτάται από τον τρόπο κωδικοποίησης του ψηφιακού σήματος και το είδος της διαμόρφωσης που θα επιλεγεί. Μετριέται σε bits/sec/Hz.
Με βάση τα παραπάνω, είναι προφανές ότι η διαμόρφωση PSK είναι πιό αποτελεσματική από την FSK και την OOK.
Διερευνώντας τις τρεις διαμορφώσεις OOK, FSKκαι PSK σχετικά με τις επιδόσεις τους στο θόρυβο αποδεικνύεται ότι η διαμόρφωση PSK είναι καλύτερη. Για το ίδιο ποσοστό σφάλματος δυαδικών στοιχείων στην έξοδο (biterrorrate) η PSK απαιτεί μισή ισχύ σήματος στην είσοδο του δέκτη. Η αναλυτική μελέτη των επιδόσεων των ψηφιακών διαμορφώσεων σε σχέση με το θόρυβο ξεφεύγει από το πλαίσιο αυτού του μαθήματος.
Εφαρμογή 1: Σε διαμόρφωση ΟΟΚ η ολική φασματική ζώνη του φέροντος δεν πρέπει να ξεπεράσει τα 100 kHz. Να προσδιοριστεί ο μέγιστος ρυθμός δυαδικών συμβόλων σε bits/secπου μπορούμε να έχουμε.
Λύση: Στην περίπτωση της ΟΟΚ ισχύει: Βολ = 1,6R, όπου Ro ρυθμός bits/sec. Έτσι, R = 100000/1,6 = 62500 bits/sec.
Εφαρμογή 2: Σε δεδομένη εφαρμογή με διαμόρφωση FSK χρησιμοποιούνται ταλαντωτές με συχνότητες f1 = 1800 Hz (που αντιπροσωπεύει το δυαδικό στοιχείο ‘1’ ) και f2 = 1200 Hz (που αντιπροσωπεύει το δυαδικό στοιχείο ‘0’ ). Ο ρυθμός μετάδοσης στο κανάλι είναι 1200 bauds. Να προσδιοριστεί το φασματικό εύρος του σήματος στο τηλεπικοινωνιακό κανάλι.
Λύση: Αναφερόμενοι στο σχήμα 9.2.6 ισχύει: Bολ = 2Β + 2Δf.
B = 0,8Rs = 0,8R = 0,8 . 1200 = 960 Hzκαι 2Δf = f1 – f2 = 600 Hz.
Άρα, Βολ = 2 . 960 + 600 = 2520 Hz.