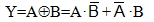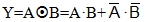1.3 ΛΟΓΙΚΕΣ ΠΥΛΕΣ
1.3.1 Λογικά διαγράμματα των λογικών πυλών
Οι λογικές πύλες είναι τα βασικά δομικά στοιχεία στα ψηφιακά κυκλώματα. Όπως έχουμε στις οικοδομές τα τούβλα και με αυτά κατασκευάζουμε τοίχους και σύνθετες κατασκευές χρησιμοποιώντας παρόμοια υλικά ξανά και ξανά, έτσι και στα ψηφιακά κυκλώματα χρησιμοποιούμε τις λογικές πύλες για να κατασκευάσουμε σύνθετα κυκλώματα.
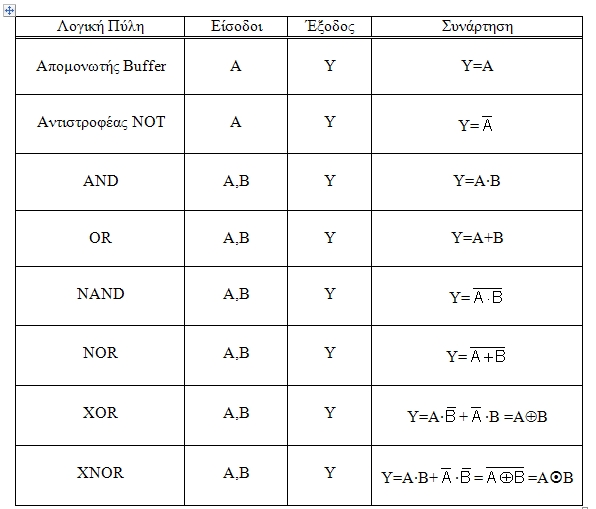
Οι λογικές πύλες μίας και δύο εισόδων παρουσιάζονται στον Πίνακα 1.3.1 όπου η έξοδος εκφράζεται ως συνάρτηση των εισόδων.
Πίνακας 1.3.1
Λογικές Πύλες - Συναρτήσεις
Τα λογικά διαγράμματα (οι συμβολισμοί) των πυλών αυτών παρουσιάζονται στον Πίνακα 1.3.2.
Πίνακας 1.3.2
Λογικές Πύλες – Λογικά Διαγράμματα
1.3.2 Πίνακες αληθείας των λογικών πυλών
Ο απομονωτής (buffer)
O απομονωτής (buffer) είναι μία πύλη με μία είσοδο και μία έξοδο που είναι ίση με την είσοδο.
Η συνάρτηση του απομονωτή είναι:
Y=A
και ο πίνακας αληθείας του απομονωτή παρουσιάζεται στον Πίνακα 1.3.3.
Πίνακας 1.3.3
Πίνακας αληθείας του απομονωτή
|
A |
Y=A |
|
0 |
0 |
|
1 |
1 |
Η πύλη NOT
Η πύλη NOT έχει μία είσοδο και μία έξοδο που είναι ίση με το συμπλήρωμα της εισόδου.
Η συνάρτηση της πύλης NOT είναι:
και ο πίνακας αληθείας της πύλης NOT παρουσιάζεται στον Πίνακα 1.3.4.
Πίνακας 1.3.4
Πίνακας αληθείας της πύλης NOT

Η πύλη AND
Η πύλη AND έχει δύο εισόδους και μία έξοδο που είναι “1”, αν και οι δύο είσοδοι είναι “1”.
Η συνάρτηση της πύλης AND είναι:
Y=A·B
και ο πίνακας αληθείας της πύλης AND παρουσιάζεται στον Πίνακα 1.3.5.
Πίνανας 1.3.5
Πίνακας Αληθείας της πύλης AND
|
A |
B |
Y=A·B |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Η πύλη OR
Η πύλη OR έχει δύο εισόδους και μία έξοδο που είναι “1”, αν τουλάχιστον μία από τις δύο εισόδους είναι “1”.
Η συνάρτηση της πύλης OR είναι:
Y=A+B
και ο πίνακας αληθείας της πύλης OR παρουσιάζεται στον Πίνακα 1.3.6.
Πίνανας 1.3.6
Πίνακας Αληθείας της πύλης OR
|
A |
B |
Y=A+B |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
Η πύλη NAND
Η πύλη NAND προκύπτει από μία πύλη AND ακολουθούμενη από μία πύλη NOT. Η πύλη NAND έχει δύο εισόδους και μία έξοδο που είναι “1”, αν τουλάχιστον μία από τις δύο εισόδους είναι “0”.
Η συνάρτηση της πύλης NAND είναι:
και ο πίνακας αληθείας της πύλης NAND παρουσιάζεται στον Πίνακα 1.3.7.
Πίνανας 1.3.7
Πίνακας Αληθείας της πύλης NAND
|
A |
B |
 |
|
0 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
Η πύλη NOR
Η πύλη NOR προκύπτει από μία πύλη OR ακολουθούμενη από μία πύλη NOT. Η πύλη NOR έχει δύο εισόδους και μία έξοδο που είναι “1”, αν και οι δύο είσοδοι είναι “0”.
Η συνάρτηση της πύλης NOR είναι:
και ο πίνακας αληθείας της πύλης NOR παρουσιάζεται στον Πίνακα 1.3.8.
Πίνανας 1.3.8
Πίνακας Αληθείας της πύλης NOR
|
A |
B |
 |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
0 |
Η πύλη XOR
Η πύλη XOR (exclusive OR) έχει δύο εισόδους και μία έξοδο που είναι “1”, αν οι δύο είσοδοι είναι διαφορετικές μεταξύ τους (για αυτό ονομάζεται και πύλη διαφωνίας ή σύγκρισης).
Η συνάρτηση της πύλης XOR είναι:
και ο πίνακας αληθείας της πύλης XOR παρουσιάζεται στον Πίνακα 1.3.9.
Πίνανας 1.3.9
Πίνακας Αληθείας της πύλης XOR
|
A |
B |
|
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
Η πύλη XNOR
Η πύλη XNOR (exclusive NOR) έχει δύο εισόδους και μία έξοδο που είναι “1”, αν οι δύο είσοδοι είναι ίσες.
Η συνάρτηση της πύλης XNOR είναι:
και ο πίνακας αληθείας της πύλης XNOR παρουσιάζεται στον Πίνακα 1.3.10.
Πίνανας 1.3.10
Πίνακας Αληθείας της πύλης XNOR
|
A |
B |
|
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
1.3.3 Λογικές πύλες πολλαπλών εισόδων
Οι πύλες δύο εισόδων μπορούν να επεκταθούν ώστε να έχουν περισσότερες από δύο εισόδους, εάν οι πράξεις τους έχουν την αντιμεταθετική και την επιμεριστική ιδιότητα. Η υλοποίηση μίας τέτοιας πύλης τριών (3) εισόδων με χρήση ομοίων πυλών δύο (2) εισόδων παρουσιάζεται στο Σχήμα 1.3.1.

Σχήμα 1.3.1
Τεχνική επέκτασης εισόδων πυλών
αν ισχύει η αντιμεταθετική και η επιμεριστική ιδιότητα
Για παράδειγμα, μία πύλη AND τριών εισόδων μπορεί να υλοποιηθεί χρησιμοποιώντας δύο πύλες AND δύο εισόδων όπως φαίνεται στο Σχήμα 1.3.2, γιατί ισχύει:
- η αντιμεταθετική ιδιότητα
Y=A·B=B·A
- η προσεταιριστική ιδιότητα
Y=A·B·C=(A·B)·C=A·(B·C)
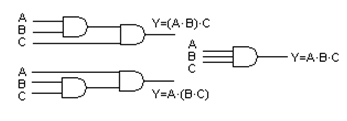
Σχήμα 1.3.2
Υλοποίηση πύλης AND τριών εισόδων
με πύλες AND δύο εισόδων
Με την ίδια λογική, μία πύλη OR τριών εισόδων μπορεί να υλοποιηθεί χρησιμοποιώντας δύο πύλες OR δύο εισόδων όπως φαίνεται στο Σχήμα 1.3.3.

Σχήμα 1.3.3
Υλοποίηση πύλης OR τριών εισόδων
με πύλες OR δύο εισόδων
Η πύλη NAND τριών εισόδων ορίζεται ως το συμπλήρωμα της πύλης AND τριών εισόδων. Επομένως, η έξοδος της πύλης NAND τριών εισόδων είναι “1”, αν τουλάχιστον μία από τις δύο εισόδους είναι “0”.
Μία πύλη NAND τριών εισόδων δεν μπορεί να υλοποιηθεί χρησιμοποιώντας δύο πύλες NAND δύο εισόδων, γιατί ισχύει η αντιμεταθετική ιδιότητα, αλλά δεν ισχύει η προσεταιριστική ιδιότητα αφού:
όπως φαίνεται στον Πίνακα 1.3.11.
Πίνακας 1.3.11
Πύλη NAND: δεν ισχύει η προσεταιριστική ιδιότητα
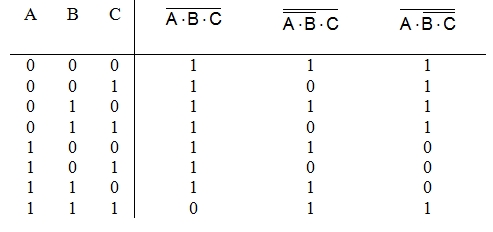
Με την ίδια λογική, μία πύλη NOR τριών εισόδων δεν μπορεί να υλοποιηθεί χρησιμοποιώντας δύο πύλες NOR δύο εισόδων.
Η λογική της επέκτασης του πλήθους των εισόδων των πυλών, μπορεί να εφαρμοστεί και για πύλες τεσσάρων εισόδων.
Για παράδειγμα, μία πύλη AND τεσσάρων εισόδων μπορεί να υλοποιηθεί χρησιμοποιώντας τρεις πύλες AND δύο εισόδων και μία πύλη OR τεσσάρων εισόδων μπορεί να υλοποιηθεί χρησιμοποιώντας τρεις πύλες OR δύο εισόδων.