6.3.4 Τ FLIP-FLOP
Αν οι είσοδοι του J-K flip-flop συνδεθούν μεταξύ τους, τότε προκύπτει μία παραλλαγή του J-K flip-flop, το Τ flip-flop.
Το Τ flip-flop μπορεί να υλοποιηθεί χρησιμοποιώντας ένα J-K flip-flop συνδέοντας τις εισόδους J και Κ, όπως φαίνεται στο Σχήμα 6.3.7.

Σχήμα 6.3.7 Τ flip-flop
Η λειτουργία του Τ flip-flop περιγράφεται παρακάτω:
- Οταν Τ=0, τότε η επόμενη κατάσταση είναι ίδια με την προηγούμενη κατάσταση.
- Οταν Τ=1, τότε η κατάσταση του flip-flop αντιστρέφεται, δηλαδή η επόμενη κατάσταση είναι η συμπληρωματική της προηγούμενης κατάστασης.
Το όνομα του Τ flip-flop προέρχεται από τη δυνατότητα του να αντιστρέφει (Toggle) την κατάσταση του.
Ο χαρακτηριστικός πίνακας του Τ flip-flop παρουσιάζεται στον Πίνακα 6.3.7.
Πίνακας 6.3.7 Χαρακτηριστικός Πίνακας Τ flip-flop
|
Q(n) Τ |
Q(n+1) |
|
0 0 |
0 |
|
0 1 |
1 |
|
1 0 |
1 |
|
1 1 |
0 |
ή εν συντομία
|
τ |
Q(n+1) |
|
0 1 |
Q(n) Q(n)' |
Το Q(n)' είναι το συμπλήρωμα του Q(n)
Ο πίνακας διέγερσης του Τ flip-flop παρουσιάζεται στον Πίνακα 6.3.8.
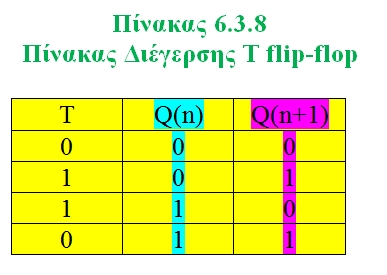
Πίνακας 6.3.8 Πίνακας Διέγερσης Τ flip-flop
To γραφικό σύμβολο του Τ flip-flop φαίνεται στο Σχήμα 6.3.8.
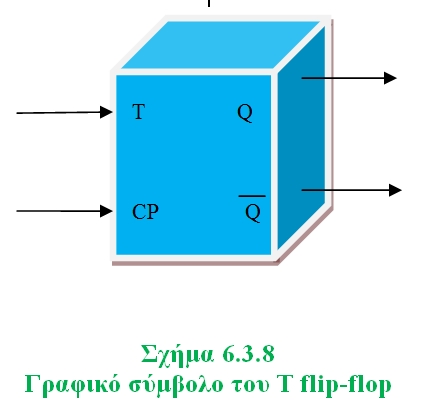
Σχήμα 6.3.8 Γραφικό σύμβολο του Τ flip-flop

