|
Τριχοτόμηση Γωνίας -Η
πρώτη λύση του Πάππου |
||
|
Ο Πάππος στο έργο του "Μαθηματική συναγωγή" έδωσε δύο λύσεις στο πρόβλημα της τριχοτόμησης μιας γωνίας. Τη μία από αυτές παρουσιάζουμε παρακάτω. |
||
|
||
|
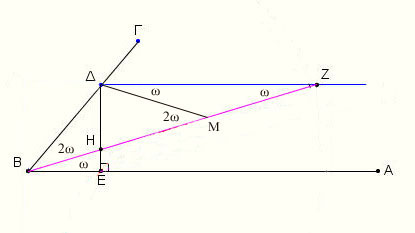
Η γωνία ΔΖΒ=ΖΒΑ λόγω των παραλλήλων ΔΖ//ΒΑ, η γωνία ΜΔΖ=ΜΖΔ επειδή το τρίγωνο ΜΔΖ είναι ισοσκελές.
|
||
|
Το πρόβλημα τώρα είναι, πως θα κατασκευάσουμε το τμήμα ΗΖ ώστε, να έχει τα άκρα του πάνω στις γνωστές ευθείες ΔΕ και ΔΖ να έχει μήκος 2ΒΔ και η προέκταση του να διέρχεται από το Β. Το πρόβλημα αυτό, της κατασκευής ενός τμήματος με δεδομένο μήκος του οποίου να άκρα να βρίσκονται σε γνωστές γραμμές και το ίδιο ή προεκτεινόμενο να διέρχεται από γνωστό σημείο, ήταν γνωστό στους αρχαίους ως κατασκευή νεύσεως ή απλά νεύσις . |
||
| Ο Παππος έλυσε την παραπάνω νεύση ως εξής. | ||
|
||
|
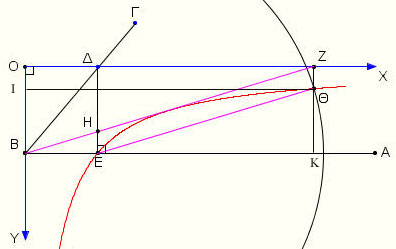
Από την (1) προκύπτει η ΗΕ·ΟΖ =ΕB·ΕΔ και επειδή ΗΕ=ΘΖ και ΟΖ=ΘΙ έχουμε ΘΖ·ΘΙ=ΕΒ·ΕΔ (2) . Από την (3) προκύπτει ότι, το σημείο Θ ανήκει σε μια γνωστή υπερβολή και επειδή ΕΘ =ΗΖ=2ΒΔ θα ανήκει επίσης και στον κύκλο με κέντρο το Ε και ακτίνα 2ΒΔ, έτσι το σημείο Θ κατασκευάζεται ως τομή της υπερβολής και του κύκλου. | ||
| Από την παραπάνω ανάλυση προκύπτει ότι για την κατασκευή του ΗΖ πρέπει να : | ||
|
||
| Τα παραπάνω φαίνονται στην εφαρμογή που ακολουθεί. Πατήστε το πλήκτρο "Start" μέχρι να γράψει "Τέλος" . | ||
| Βιβλιογραφία | ||
|
|
||
|
Η λύση του : Αρχιμήδη-1, Αρχιμήδη-2, Πάππου-1, Πάππου -2 , Ιππία, Νικομήδη, Pascal |
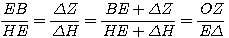 (1).
(1).