|
Τριχοτόμηση
Γωνίας -Η λύση του
Blaise Pascal |
||
|
||
| Ο Pascal παρατήρησε ότι στην ειδική περίπτωση πού πάρουμε το τμήμα α ίσο με την ακτίνα του κύκλου μπορούμε να τριχοτομήσουμε μια γωνία όπως περιγράφεται παρακάτω .Διαβάστε τις οδηγίες για το σχηματισμό του σχήματος | ||
|
|
||
| Για την απόδειξη των παραπάνω έχουμε : | ||
Επειδή η
ΚΔ είναι κάθετη στη ΟΓ είναι
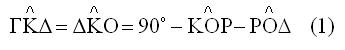 |
||
| Η ΓΚΖ
γωνία είναι επίκεντρη και βαίνει στο ίδιο τόξο με την εγγεγραμμένη ΓΟΖ άρα
θα είναι |
||
| Το σημείο Ρ ανήκει στην κοχλιοειδή καμπύλη άρα ΖΡ=ΖΚ δηλ το τρίγωνο ΡΚΖ είναι ισοσκελές και επειδή η γωνία ΚΡΖ είναι κατακορυφήν με την ΔΡΟ θα είναι | ||
|
|
||
| Είναι
επίσης
|
||
|
Εξισώνοντας τα δεύτερα μέλη των (3) και (4) προκύπτει |
||
| Η γωνία ΑΚΒ είναι εξωτερική στο ισοσκελές τρίγωνο ΟΚΓ άρα ισχύει λόγω και της (5). | ||
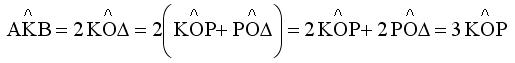 |
||
Άρα
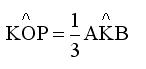 |
||
| Βιβλιογραφία | ||
|
Η λύση του : Αρχιμήδη-1, Αρχιμήδη-2, Πάππου -1, Πάππου -2 , Ιππία, Νικομήδη, Pascal |