ΘΕΜΑΤΑ ΘΕΩΡΙΑΣ ΑΕΠΠ

Για την είσοδο δεδομένων σε κάποιον αλγόριθμο μπορούν να χρησιμοποιηθούν οι εντολές:

i. Διάβασε, π.χ ΔΙΑΒΑΣΕ Χ
ii. Δεδομένα, π.χ. Δεδομένα // x //

Για την εκχώρηση τιμής στην μεταβλητή χ μπορούν να χρησιμοποιηθούν η εντολή
ΔΙΑΒΑΣΕ π.χ. ΔΙΑΒΑΣΕ Χ
και η
εντολή εκχώρησης π.χ. x<-- 12

Κάθε αλγόριθμος πρέπει απαραίτητα να ικανοποιεί το κριτήριο της εξόδου, όχι όμως απαραίτητα και το κριτήριο της εισόδου

Για την έξοδο δεδομένων σε κάποιον αλγόριθμο μπορούν να χρησιμοποιηθούν οι εντολές:

i. Εκτύπωσε, για έξοδο στον εκτυπωτή
ii. Εμφάνισε, για έξοδο στην οθόνη
iii. Αποτελέσματα, για έξοδο με άλλο τρόπο

ΤΙ ΔΕΝ ΙΚΑΝΟΠΟΙΟΥΝ;

Αλγόριθμος Παράδειγμα 1
x <-- 7
y <-- 2 * x
Τέλος Παράδειγμα
ΕΞΌΔΟΥ

 Αλγόριθμος Παράδειγμα 2
  Διάβασε x
  y <-- 5 / x
  Εμφάνισε y
Τέλος Παράδειγμα2
καθοριστικότητα

Αλγόριθμος Παράδειγμα3
  Διάβασε α, β
  γ <-- μεγιστο(α, β)  
  Εμφάνισε γ
Τέλος Παράδειγμα3
αποτελεσματικότητα (εφόσον δεν έχει οριστεί η συνάρτηση)

Αλγόριθμος Παράδειγμα4
 ΓΙΑ Κ ΑΠΟ 1 ΜΕΧΡΙ 100
 Διάβασε α, β
 Λ<--Λ+1 
  Εμφάνισε Λ
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
Τέλος Παράδειγμα3
αποτελεσματικότητα 
ακόμα και να έχει δηλωθεί το Λ δεν έχει αρχική τιμή 
για την εκχώρηση Λ<--Λ+1

Αλγόριθμος Παράδειγμα5
  Διάβασε Α
  Σ <-- 0
  Για i από 1 μέχρι 10 με_βήμα Α
    Σ <-- Σ + i
  Τέλος_επανάληψης
  Αποτελέσματα // Σ //
Τέλος Παράδειγμα5

περατότητας αφού αν διαβαστεί Α=0 δεν τελειώνει ποτέ

Πολ/σμός αλά ρωσικά

Είναι μία μέθοδος πολλαπλασιασμού δύο αριθμών. Συγκεκριμένα, αν έχουμε δύο αριθμούς Μ1 και Μ2 και θέλουμε το Μ1*Μ2 τότε αυτό γίνεται ως εξής:

Βήμα 1 Ο Μ1 διπλασιάζεται και ο Μ2 υποδιπλασιάζεται. (Ακέραια διαίρεση με το 2)

Βήμα 2 Συνεχίζουμε το Βήμα 1 μέχρι να φτάσει ο Μ2 σε 1.

Βήμα 3 Το γινόμενο θα είναι το άθροισμα των στοιχείων Μ1 στις περιπτώσεις που το Μ2 είναι περιττός.

Μ1 Μ2 Σ

20	10
40	5	40
80	2
160	1	160
Άθροισμα=		200

Αλγόριθμος Πολ/σμός_αλά_ρωσικά

ΔΕΔΟΜΕΝΑ// Μ1,Μ2 //
Αρχή
        Σ<--0
         Οσο Μ2>0 επανάλαβε
         Αν (Μ2 MOD 2) = 1
τότε
                       Σ <-- Σ + Μ1
                 τέλος_αν
                   Μ1 <-- Μ1 * 2
                   Μ2 <-- Μ2 DIV 2
         τέλος_επανάληψης
        ΑΠΟΤΕΛΕΣΜΑΤΑ // Σ//
τέλος_Πολ/σμός_αλά_ρωσικά

Ποια η πρακτική σημασία της μεθόδου αυτής ;
Διότι στους Η/Υ , σε επίπεδο κυκλωμάτων είναι πολύ δύσκολο να κάνουμε τον πολλαπλασιασμό παραδοσιακά.
Με την μέθοδο αυτή απαιτείται διπλασιασμός και υποδιπλασιασμός που υλοποιείται πολύ απλά και ταχύτατα με την εντολή της ολίσθησης (shift).

Τ Α Ξ Ι Ν Ο Μ Η Σ Η

Έστω ο πίνακας Π=[4 , 15 ,12, 3 , 9] και θέλουμε να τον μετατρέψουμε σε

Π=[ 3,4 ,9 ,12,15 ]

i=2 α΄πέρασμα					i=3 β΄πέρασμα			i=4 γ΄πέρασμα		i=5 δ΄πέρασμα
σ υ γ κ ρ ί σ ε ι ς	j=5	j=4	j=3	j=2	j=5	j=4	j=3	j=5	j=4	j=5
	4	4	4	3	3	3	3	3	3	3
	15	15	3	4	4	4	4	4	4	4
	12	3	15	15	15	9	9	9	9	9
	3	12	12	12	9	15	15	12	12	12
	9	9	9	9	12	12	12	15	15	15

τα παραπάνω περάσματα τα υλοποιεί μια επανάληψη Για i από 2 μέχρι Ν=5
και τις παραπάνω συγκρίσεις μια άλλη επανάληψη Για j από Ν μέχρι i με_βήμα -1
αν και ο πίνακας είναι μονοδιάστατος θα χρειαστούμε δύο εμφωλευμένες επαναλήψεις

Ταξινόμηση Φυσσαλίδας
ή
ευθείας ανταλλαγής

Δίνεται ένας πίνακας Π, Ν στοιχείων, να εξεταστεί αν είναι ταξινομημένος κατά φθίνουσα σειρά. Αν είναι να εμφανίζεται μήνυμα , διαφορετικά να ταξινομείται

Αλγόριθμος έξυπνη φυσαλίδα

Ο αλγόριθμος Ταξινόμηση Φυσσαλίδας όπως φαίνεται στην α΄στήλη, δεν είναι αρκετά έξυπνος γιατί αν τα στοιχεία του ήταν ταξινομημένα από την αρχή ή κατά την διάρκεια της ταξινόμησης αυτός δεν σταματά αλλά συνεχίζει με όλες τις επαναλήψεις
Να σχεδιάσετε μια παραλλαγή του ώστε να σταματά όταν διαπιστωθεί ότι τα στοιχεία του Π είναι ήδη ταξινομημένα

Αλγόριθμος Ταξινόμηση_Φυσσαλίδας
Δεδομένα // Π, Ν //
Για i από2 μέχρι Ν
Για j απόΝ μέχρι i με_βήμα -1
! αύξουσα ταξινόμηση

Αν Π[j-1] > Π[j] τότε

Τ<-- Π[j-1]

Π[j-1] <-- Π[j]

Π[j] <-- Τ

Τέλος_αν
Τέλοςεπανάληψης
Τέλοςεπανάληψης
Αποτελέσματα // Π, Ν //

Τέλος Ταξινόμηση_Φυσσαλίδας

Παρατήρηση 1
Η τριάδα εντολών
Τ<-- Π[j-1]
Π[j-1] <-- Π[j]
Π[j] <-- Τ
μπορεί να αντικατασταθεί με την
αντιμετάθεσε Π[j-1] , Π[j]

Παρατήρηση2
αν Π είναι πίνακας ακεραίων και ΟΝ είναι παράλληλος πίνακας ονομάτων τότε με τις εντολές:
...
Αν Π[j-1] > Π[j] τότε
Τ<-- Π[j-1]
Π[j-1] <-- Π[j]
Π[j] <-- Τ

Τ<-- ΟΝ[j-1]
ΟΝ[j-1] <-- ΟΝ[j]
ΟΝ[j] <-- Τ
φαίνεται ότι ταξινομούνται κατά αύξουσα σειρά οι πίνακες Π , ΟΝ με κριτήριο ταξινόμησης τα στοιχεία του Π
όμως είναι λάθος αφού χρησιμοποιούμε την βοηθητική μεταβλητή Τ τόσο για ακέραια στοιχεία όσο και για χαρακτήρες. Το σωστό είναι να χρησιμοποιήσουμε Τ1 για την β΄αντιμετάθεση

Παρατήρηση3

...
Αν Π[j-1] > Π[j] τότε
Τ<-- Π[j-1]
Π[j-1] <-- Π[j]
Π[j] <-- Τ

ΤΕΜP<-- ΟΝ[j-1]
ΟΝ[j-1] <-- ΟΝ[j]
ΟΝ[j] <-- ΤΕΜP
ΑΛΛΙΩΣ ΑΝ Αν Π[j-1]= Π[j] ΤΟΤΕ
Αν ΟΝ[j-1] > ΟΝ[j] τότε `
ΤΕΜP<-- ΟΝ[j-1]
ΟΝ[j-1] <-- ΟΝ[j]
ΟΝ[j] <-- ΤΕΜP
εδώ ταξινομούνται κατά αύξουσα σειρά οι πίνακες Π , ΟΝ με κριτήριο ταξινόμησης τα στοιχεία του Π και αν κάποια στοιχεία του Π είναι ίδια η ταξινόμηση συνεχίζει αλφαβητικά για τον πίνακα ΟΝ

Δεδομένα // Π, Ν //

κ<-- 0

Για i από2 μέχρι Ν

Για j απόΝ μέχρι i με_βήμα -1
! φθίνουσα ταξινόμηση

      Αν Π[j-1] < Π[j] τότε
     Τ<-- Π[j-1]
     Π[j-1] <-- Π[j]
      Π[j] <-- Τ
        κ<-- κ+1
     Τέλος_αν

Τέλοςεπανάληψης
Τέλοςεπανάληψης
Αποτελέσματα // Π, Ν //

Αν κ=0 τότε
εμφάνισε " είναι ταξινομημένος"
Αλλιώς
εμφάνισε "Ταξινομήθηκε"
Τέλος_αν

Τέλος Ταξινόμηση_Φυσαλίδας

Δεδομένα // Π, Ν //
! Πρέπει να αλλάξουμε την α΄ δομή επανάληψης
α <--αληθής
i <--2
ΟΣΟ i <=N και α = αληθής ΕΠΑΝΑΛΑΒΕ
α <--ψευδής
Για j από Ν μέχρι i με_βήμα -1
Αν Π[j-1] > Π[j] τότε

Τ<-- Π[j-1]

Π[j-1] <-- Π[j]

Π[j] <-- Τ
α <--αληθής

Τέλος_αν
Τέλοςεπανάληψης
i <-- i+1
Τέλοςεπανάληψης
Αποτελέσματα // Π, Ν //

Τέλος Ταξινόμηση_Φυσσαλίδας

Συμπληρώστε τα παρακάτω με τις λέξεις
Συντάκτης, Συντακτικά ,Λογικά , Βιβλιοθήκες πηγαίο, εκτελέσιμο, Μεταγλωττιστής, Διερμηνευτής, Συνδέτης.

1.Το ………………. πρόγραμμα είναι γραμμένο σε μία γλώσσα προγραμματισμού υψηλού επιπέδου

2. Το ………………… πρόγραμμα μπορεί αμέσως να εκτελεστεί από τον υπολογιστή.

3. Ο ………………….. παίρνει μία-μία τις .εντολές του πηγαίου προγράμματος, τις μεταφράζει και τις εκτελεί.

4. Ο ……………. μεταφράζει όλο το πηγαίο πρόγραμμα σε αντικείμενο

5. Ο ……………… είναι εκείνο το βοηθητικό πρόγραμμα με το οποίο συντάσσουμε τα προγράμματα.

6. Οι …………………….. αποτελούν έτοιμες ενότητες αντικείμενου προγράμματος.

7. Η παραγωγή του εκτελέσιμου προγράμματος γίνεται από τον ………………………………….

8. Τα ……………………….. λάθη ανιχνεύονται από τον μεταφραστή ή διερμηνέα αλλά τα …………… δεν μπορούν να ανιχνευθούν εύκολα και αφορούν σφάλματα στη λογική επίλυσης.

Αντιστοιχίστε κάθε ένα από τα προβλήματα της Α στήλης με ένα ή περισσότερα από τα υποπρογράμματα της Β στήλης που μπορούν να χρησιμοποιηθούν για την επίλυσή τους.

ΣΤΗΛΗ Α	ΣΤΗΛΗ Β
1. Υπολογισμός του μεγίστου δύο αριθμών.	Α. Διαδικασία
2. Υπολογισμός της απόλυτης τιμής ενός αριθμού.	Α. Διαδικασία
3. Εύρεση των ψηφίων ενός αριθμού	Β. Συνάρτηση
4. Υπολογισμός εμβαδού και περιμέτρου ενός κύκλου.	Β. Συνάρτηση

1 Α&Β 2 Α& Β 3 A 4 Α

Στήλη Α Είδος εφαρμογών	Στήλη Β Γλώσσες
1. επιστημονικές	α. COBOL
2. εμπορικές επιχειρησιακές	β. LISP
3. τεχνητής νοημοσύνης	γ. FORTRAN
4. γενικής χρήσης- εκπαίδευσης	δ. PASCAL
	ε. JAVA

1.γ, 2.α, 3.β, 4.δ

Να γράψετε στο τετράδιό σας τους αριθμούς 1,2,3,4 της Στήλης Α και δίπλα ένα από τα γράμματα α,β,γ,δ,ε,στ της Στήλης Β που αντιστοιχεί στον σωστό ορισμό.
Στήλη Α	Στήλη Β
1. Προσθήκη νέων κόμβων σε μία υπάρχουσα δομή.	α. Προσπέλαση β. Αντιγραφή γ. Διαγραφή δ. Αναζήτηση ε. Εισαγωγή στ. Ταξινόμηση
2. Οι κόμβοι μιας δομής διατάσσονται κατά αύξουσα ή φθίνουσα σειρά.
3. Πρόσβαση σε ένα κόμβο με σκοπό να εξετασθεί ή να τροποποιηθεί το περιεχόμενό του.
4. Όλοι οι κόμβοι ή μερικοί από τους κόμβους μιας δομής αντιγράφονται σε μία άλλη δομή.

ΣΗΜΕΙΩΣΗ: Δύο (2) στοιχεία της Στήλης Β δεν χρησιμοποιούνται

1ε 2στ 3α 4β

Δίδονται τα παρακάτω βήματα ενόςαλγορίθμου:

α. τέλος
β. διάβασε δεδομένα
γ. εμφάνισε αποτελέσματα
δ. αρχή
ε. κάνε υπολογισμούς

Να τοποθετηθούν στη σωστή σειρά με την οποία εμφανίζονται συνήθως σε αλγορίθμους

δ β ε γ α

Αριθμείστε – ταξινομείστε σωστά τα παρακάτω :

Σώμα εντολών
Μεταβλητές
Πρόγραμμα όνομα
Τέλος προγράμματος
Διαδικασίες
Τμήμα δηλώσεων
Σταθερές

3 6 7 2 1 4 5

Σωστό ή Λάθος

1. Ένα υποπρόγραμμα δεν μπορεί να κληθεί περισσότερες από δυο φορές από το κυρίως πρόγραμμα.

2. Οι διαδικασίες επιτρέπεται να μεταβάλλουν τις τιμές των παραμέτρων που δέχονται από το κυρίως πρόγραμμα.

3. Μια διαδικασία μπορεί να μην έχει καμία παράμετρο.

4. Ένα υποπρόγραμμα μπορεί κατά την εκτέλεσή του να καλέσει το κυρίως πρόγραμμα.

5. Στα υποπρογράμματα δεν είναι απαραίτητη η δήλωση των μεταβλητών που χρησιμοποιούν, αν αυτές έχουν το ίδιο όνομα και τύπο με μεταβλητές του κυρίως προγράμματος.

6. Υπάρχει η περίπτωση τυπικές και πραγματικές παράμετροι να έχουν το ίδιο όνομα και διαφορετικό τύπο.
τα παραπάνω είναι: Λ Σ Σ Λ Λ Λ

Όλες οι μεταβλητές του κύριου προγράμματος είναι και παράμετροι.
Η αναφορά σε ένα στοιχείο ενός δισδιάστατου πίνακα γίνεται με τη χρήση δύο δεικτών οι οποίοι είναι υποχρεωτικά φυσικοί αριθμοί.
Στην δομή της ουράς, όταν οι δείκτες Εμπρός και Πίσω έχουν την τιμή 7, η ουρά έχει 7 στοιχεία.
Ο δομημένος προγραμματισμός βασίζεται στη χρήση του Goto (πήγαινε) σε συνδυασμό με την ιεραρχική σχεδίαση.
Μια διαδικασία δεν μπορεί να καλεί στο τμήμα των εντολών της κάποια συνάρτηση.
Η προτεραιότητα των συγκριτικών τελεστών είναι μικρότερη των λογικών.
Η ουρά είναι μια δομή δεδομένων όπου η επεξεργασία πραγματοποιείται και από τα δυο άκρα.
Η δημιουργία του εκτελέσιμου προγράμματος γίνεται μόνο όταν το πηγαίο πρόγραμμα δεν περιέχει συντακτικά λάθη.
Ένας από τους λόγους ανάθεσης ενός προβλήματος σε υπολογιστή είναι η πολυπλοκότητα των υπολογισμών.
Η σειριακή αναζήτηση είναι ο πιο γρήγορος αλγόριθμος αναζήτησης.
τα παραπάνω είναι: Λ Σ Λ Λ Λ Λ Σ Λ Σ Λ

Η εντολή Όσο χ < 1 Επανάλαβε δεν είναι έγκυρη
Αν η συνθήκη στη δομή Αρχή_επανάληψης..... μέχρις_ότου γίνει αληθής κατά το δεύτερο έλεγχο τότε οι εσωτερικές εντολές θα εκτελεστούν δύο φορές
Στους εμφωλευμένους βρόχους επανάληψης ο εσωτερικός βρόχος κλείνει μετά τον εξωτερικό
Ο πολλαπλασιασμός αλά Ρωσικά χρησιμοποιεί επαναληπτικά την πράξη της πρόσθεσης και της ολίσθησης.
Ο βρόχος για i από x μέχρι y με_βήμα -1 δεν θα εκτελεστεί καμία φορά αν η τιμή x είναι μεγαλύτερη από την τιμή y

Απαγορεύεται σε ένα υποπρόγραμμα να γίνεται κλήση ενός άλλου υποπρογράμματος.
τα παραπάνω είναι: Σ Λ Λ Σ Λ Λ
Υπάρχουν ειδικές περιπτώσεις κατά τις οποίες μια συνάρτηση μπορεί να επιστρέψει ταυτόχρονα και
με τις ίδιες παραμέτρους στο κυρίως πρόγραμμα δυο διακριτές τιμές.
Ο τμηματικός προγραμματισμός χρησιμοποιείται για να κάνει τα προγράμματα να εκτελούνται ταχύτερα.
Στον κώδικα υλοποίησης μιας Συνάρτησης, το όνομά της πρέπει οπωσδήποτε να βρίσκεται τουλάχιστον μια φορά στο αριστερό τμήμα εντολής εκχώρησης.
Οι εντολές μέσα στη δομή επανάληψης «Για x από 10 μέχρι 3 με_βήμα - 3» εκτελούνται 3 φορές
Το βήμα στην εντολή Για … από … μέχρι, πρέπει να είναι πάντα ακέραιος αριθμός.
τα παραπάνω είναι: Λ Λ Σ Λ Λ
Μια δομή επανάληψης η οποία εκτελείται έπ’ αόριστον ονομάζεται ατέρμων βρόχος
Στην εντολή Αρχή_επανάληψης … Μέχρις_ότου αν η συνθήκη είναι ψευδής οι εντολές δε θα εκτελεστούν καμία φορά.
Στην επαναληπτική εντολή Για η τελική τιμή του μετρητή είναι πάντα μεγαλύτερη ή ίση από την αρχική.
Όλες οι δομές επανάληψης μπορούν να μετατραπούν σε Όσο ... επανάλαβε.
Όταν η συνθήκη είναι ψευδής στη δομή Αρχή_επανάληψης … μέχρις_ότου το πρόγραμμα εκτελεί την επόμενη εντολή, που ακολουθεί αμέσως μετά τη δομή της επανάληψης.
Αν στη δομή επανάληψης Για … από … μέχρι το βήμα δοθεί μηδέν, τότε ο βρόχος της επανάληψης δεν εκτελείται καμία φορά.
Η σειρά εντολών στη δομή Αρχή_επανάληψης … μέχρις_ότου εκτελείται υποχρεωτικά τουλάχιστον μια φορά.
Ο βρόχος Για x από 5 μέχρι 5 με_βήμα 3 εκτελείται μία μόνο φορά.
τα παραπάνω είναι: Σ Λ Λ Σ Λ Λ Σ Σ

36. Ο πολλαπλασιασμός αλά ρωσικά είναι μία από τις βασικές λειτουργίες του υπολογιστή.
37. Οι τυπικές παράμετροι ενός υποπρογράμματος δεν μπορούν να χρησιμοποιούνται για την κλήση άλλου υποπρογράμματος.
38. Ένα σύγχρονο προγραμματιστικό περιβάλλον είναι πλήρες όταν περιλαμβάνει το συντάκτη, το μεταγλωττιστή και τις βιβλιοθήκες της γλώσσας.
39. Η ιεραρχική σχεδίαση χρησιμοποιεί ως πρωτεύοντα δομικά στοιχεία τα δεδομένα, που διαμορφώνουν τα αντικείμενα.
40. Δεσμευμένες λέξεις είναι οι λέξεις που χρησιμοποιούνται για τα ονόματα των μεταβλητών και των υποπρογραμμάτων.
41. Στη ΓΛΩΣΣΑ οι δυναμικές δομές δεδομένων υλοποιούνται όπως και οι στατικές, με πίνακες.
42.Τα προγράμματα σε γλώσσα μηχανής δε χρησιμοποιούν ούτε συμβολομεταφραστή ούτε μεταγλωττιστή για την εκτέλεσή τους από τον υπολογιστή.
43.Αναθέτουμε την επίλυση προβλημάτων στους υπολογιστές, λόγω της δυνατότητάς τους να επιτελούν πρόσθεση, σύγκριση και μεταφορά δεδομένων
τα παραπάνω είναι: Λ Λ Λ Λ Λ Λ Σ Λ

Τα προγράμματα σε γλώσσες υψηλού επιπέδου είναι ανεξάρτητα του υπολογιστή που αναπτύχθηκαν.
Ο μεταγλωττιστής μας επιτρέπει να συντάξουμε ένα πρόγραμμα.
Τα λογικά λάθη του προγράμματος εμφανίζονται κατά τη μεταγλώττιση.
Ο δομημένος προγραμματισμός επιτρέπει την άμεση μεταφορά των αλγορίθμων σε πρόγραμμα.

48. Επιλύσιμο είναι ένα πρόβλημα για το οποίο ξέρουμε ότι έχει λύση, αλλά αυτή δεν έχει βρεθείακόμη.
49. Η περατότητα ενόςαλγορίθμου αναφέρεται στο γεγονός ότι καταλήγει στη λύση του προβλήματος μετά από πεπερασμένο αριθμό βημάτων (εντολών).
50. Για να αναπαραστήσουμε τα δεδομένα και τα αποτελέσματα σ’ έναν αλγόριθμο, χρησιμοποιούμε μόνο σταθερές
τα παραπάνω είναι: Σ Λ Λ Σ Σ Λ

Ένα πρόγραμμα σε γλώσσα μηχανής είναι μια ακολουθία δυαδικών ψηφίων.
Ο μεταγλωττιστής δέχεται στην είσοδό του ένα πρόγραμμα γραμμένο σε μια γλώσσα υψηλού επιπέδου και παράγει ένα ισοδύναμο πρόγραμμα σε γλώσσα μηχανής
Το πηγαίο πρόγραμμα εκτελείται από τον υπολογιστή χωρίς μεταγλώττιση.
Ο διερμηνευτής διαβάζει μία προς μία τις εντολές του πηγαίου προγράμματο ςκαι για κάθε μια εκτελεί αμέσως μια ισοδύναμη ακολουθία εντολών μηχανής
Ένα πρόγραμμα σε γλώσσα μηχανής χρειάζεται μεταγλώττιση.

τα παραπάνω είναι: Σ Σ Λ Σ Λ

Η ταξινόμηση είναι μια από τις βασικές λειτουργίες επί των δομών δεδομένων.
Τα στοιχεία ενός πίνακα μπορούν να αποτελούνται από δεδομένα διαφορετικού τύπου.
Ένα υποπρόγραμμα μπορεί να καλείται από ένα άλλο υποπρόγραμμα ή από το κύριο πρόγραμμα.
Στην επαναληπτική δομή Όσο … Επανάλαβε δεν γνωρίζουμε εκ των προτέρων το πλήθος των επαναλήψεων.
Κατά την εκτέλεση ενός προγράμματος μπορεί να αλλάζει η τιμή και ο τύπος μιας μεταβλητής

τα παραπάνω είναι: Σωστό . Λάθος Σωστό Σωστό Λάθος

61 Oι εντολές που βρίσκονται σε μια δομή ΑΡΧΗ_ΕΠΑΝΑΛΗΨΗΣ ..... ΜΕΧΡΙΣ_ΟΤΟΥ εκτελούνται τουλάχιστον μια φορά.

62 Μία συνάρτηση είναι δυνατό να επιστρέφει μόνον ακέραιες ή πραγματικές τιμές.

63 Η δυναμική παραχώρηση μνήμης χρησιμοποιείται στις δομές των πινάκων.

64 Η λειτουργία της ώθησης σχετίζεται με τη δομή της στοίβας.

65 Σε μια λογική έκφραση, οι συγκριτικοί τελεστές έχουν χαμηλότερη ιεραρχία από τους λογικούς τελεστές.

τα παραπάνω είναι: Σ Λ Λ Σ Λ

66.Τα προβλήματα, με κριτήριο το είδος της επίλυσης που επιζητούν, διακρίνονται σε τρεις κατηγορίες: επιλύσιμα, ανοικτά και άλυτα.

67.Μια υπολογιστική διαδικασία που δεν τελειώνει μετά από συγκεκριμένο αριθμό βημάτων αποτελεί αλγόριθμο.

68.Η εγγραφή είναι δομή δεδομένων η οποία αποτελείται από πεδία που αποθηκεύουν χαρακτηριστικά.

69. Η αντικειμενοστραφής σχεδίαση εκλαμβάνει τις «ενέργειες» ως πρωτεύοντα δομικά στοιχεία ενός προγράμματος.

70.Σε μία συνάρτηση δεν επιτρέπεται η χρήση της εντολής ΔΙΑΒΑΣΕ.

τα παραπάνω είναι: Λ Λ Σ Λ Σ

71.Η μεταφορά δεδομένων είναι μία από τις λειτουργίες που εκτελεί ο υπολογιστής.

72. Ένα τμήμα αλγορίθμου που εκτελείται επαναληπτικά αποκαλείται βρόχος.

73. Όταν ένα υποπρόγραμμα καλείται από το κύριο πρόγραμμα, η διεύθυνση επιστροφής αποθηκεύεται από το μεταφραστή σε μια ουρά.

74. Οι τύποι των μεταβλητών που υποστηρίζει η ΓΛΩΣΣΑ είναι μόνο ΠΡΑΓΜΑΤΙΚΕΣ και ΑΚΕΡΑΙΕΣ.

75. Οι εντολές που βρίσκονται σε μια επανάληψη ΟΣΟ, εκτελούνται τουλάχιστον μία φορά.

τα παραπάνω είναι: Σ Σ Σσελ219 Λ Λ

73.Η ταξινόμηση φυσαλίδας είναι ο πιο απλός και ταυτόχρονα ο πιο γρήγορος αλγόριθμος ταξινόμησης.

74. Ενώ η τιμή μίας μεταβλητής μπορεί να αλλάζει κατά την εκτέλεση του προγράμματος, αυτό που μένει υποχρεωτικά αναλλοίωτο είναι ο τύπος της.

75. Το πρόγραμμα που παράγεται από το μεταγλωττιστή λέγεται εκτελέσιμο.

76. Σε μία εντολή εκχώρησης του αποτελέσματος μίας έκφρασης σε μία μεταβλητή, η μεταβλητή και η έκφραση πρέπει να είναι του ίδιου τύπου.

77. Όταν ένας βρόχος είναι εμφωλευμένος σε άλλο, ο βρόχος που ξεκινάει τελευταίος πρέπει να ολοκληρώνεται πρώτος.

τα παραπάνω είναι: Λ Σ Λ Σ Σ

78.Η ουρά και η στοίβα μπορούν να υλοποιηθούν με δομή πίνακα.

79. Η εξαγωγή (dequeue) στοιχείου γίνεται από το εμπρός άκρο της ουράς.

80.. Η απώθηση (pop) στοιχείου γίνεται από το ΄πάνω άκρο της στοίβας.

81.. Κατά τη διαδικασία της ώθησης πρέπει να ελέγχεται αν η στοίβα είναι γεμάτη.

82.. Η ώθηση (push) στοιχείου είναι μία από τις λειτουργίες της ουράς.

τα παραπάνω είναι: Σ Σ Σ Σ Λ

83. Η λογική πράξη "ή" μεταξύ δύο προτάσεων είναι ψευδής, όταν οποιαδήποτε από τις δύο προτάσεις είναι ψευδής.

84. Η FORTRAN αναπτύχθηκε ως γλώσσα κατάλληλη για την επίλυση μαθηματικών και επιστημονικών προβλημάτων.

85. Η εντολή GOTO που αλλάζει τη ροή εκτέλεσης ενός προγράμματος είναι απαραίτητη στο δομημένο προγραμματισμό.

86. Τα συντακτικά λάθη στον πηγαίο κώδικα εμφανίζονται κατά το στάδιο της μεταγλώττισής του.

87. Η Java χρησιμοποιείται ιδιαίτερα για προγραμματισμό στο Διαδίκτυο (Internet).

τα παραπάνω είναι: Λ Σ Λ Σ Σ

Μπορείτε να χρησιμοποιήσετε συνάρτηση για τα παρακάτω; Αν ναι, να γράψετε και τον τύπο της συνάρτησης.

i. Υπολογισμός του μικρότερου από πέντε διαφορετικούς ακέραιους

ii. Υπολογισμός των δυο μικρότερων από πέντε ακέραιους

iii. Έλεγχος αν δυο αριθμοί είναι ίσοι

iv. Να ταξινομεί και να επιστρέφει ταξινομημένους 5 αριθμούς

v. Έλεγχος αν ένας χαρακτήρας είναι φωνήεν ή σύμφωνο.

vi. Αναζήτηση ενός στοιχείου ενός πίνακα πραγματικών αριθμών

Απάντηση: ακέραια, οχι , λογική, όχι, λογική, πραγματική

Να αναπτύξετε πρόγραμμα σε ΓΛΩΣΣΑ το οποίο δημιουργεί:

1. Πίνακα 5 γραμμών και 7 στηλών, όπου σε κάθε θέση του, με χρήση επαναληπτικών δομών, να εισάγεται ένας αριθμός που ισούται με το άθροισμα του αριθμού γραμμής και του αριθμού στήλης της θέσης.

Απάντηση

Για κ από 1 μέχρι 5
Για λ από 1 μέχρι 7
Α[κ,λ] <--κ+λ
ΤΕ
ΤΕ

2. Μονοδιάστατο πίνακα με 10 στοιχεία, όπου σε κάθε θέση του, με χρήση επαναληπτικών δομών, να εισάγεται στην πρώτη θέση ο αριθμός 300 και σε κάθε επόμενη το μισό της τιμής της προηγούμενης, δηλαδή στη δεύτερη θέση το 150, στην τρίτη το 75 κ.ο.κ.

Β[1] <--300
Για κ από 2 μέχρι 10
Β[κ] <--Β[κ-1] /2
ΤΕ

Ανάπτυξης

Να περιγράψετε τις κύριες λειτουργίες σε μια στοίβα και να αναφέρετε τι πρέπει να ελέγχει κάθε λειτουργία, προκειμένου να μην παρουσιάζεται πρόβλημα στη λειτουργία της στοίβας

Να αναφέρετε τους κανόνες που πρέπει να ακολουθούν οι λίστες των παραμέτρων στη χρήση υποπρογραμμάτων

Να αναφέρετε τις ιδιότητες που πρέπει να διακρίνουν τα υποπρογράμματα. Να περιγράψετε μια από αυτές τις ιδιότητες

Να αναφέρετε ονομαστικά τις κατηγορίες στις οποίες διακρίνονται τα προβλήματα, με κριτήριο το είδος της επίλυσης που επιζητούν αυτά.

Να αναφέρετε δύο βασικές λειτουργίες επί των δομών δεδομένων που δεν μπορούν να χρησιμοποιηθούν στους πίνακες. Να αιτιολογήσετε την απάντησή σας.
Απάντηση
Εισαγωγή : Προσθήκη νέων κόμβων σε μια υπάρχουσα δομή
Διαγραφή : Το αντίστροφο της εισαγωγής, αφαίρεση ενός κόμβου από τη δομή
Οι πίνακες είναι Στατικές δομές δεδομένων, το ακριβές μέγεθος της απαιτούμενης κύριας μνήμης καθορίζεται κατά τη στιγμή του προγραμματισμού, οπότε δεν μπορούμε να κάνουμε Εισαγωγή, Διαγραφή

Ποια η διαφορά μεταξύ: α. μεταβλητών και παραμέτρων; β. τυπικών και πραγματικών παραμέτρων;

Για ποιο λόγο αναπτύχθηκαν οι συμβολικές γλώσσες;

Ποιος ο ρόλος του συμβολομεταφραστή;

Αναφέρατε τις περιπτώσεις που δικαιολογείται η χρήση του αλγόριθμου της σειριακής αναζήτησης.

Τι καλείται αλφάβητο μιας γλώσσας;

Από τι αποτελείται το λεξιλόγιο μιας γλώσσας;

Τι είναι το τυπικό μιας γλώσσας;

Τι είναι το συντακτικό μιας γλώσσας;

Σε ποιες στοιχειώδεις λογικές δομές στηρίζεται ο δομημένος προγραμματισμός;

Να αναφέρετε τέσσερα πλεονεκτήματα του δομημένου προγραμματισμού

ΘΕΜΑ Β 2010 επαν

Δίνεται τo παρακάτω τμήμα αλγορίθμου, στο οποίο έχουν αριθμηθεί οι γραμμές. Θεωρήστε ότι οι τιμές που εισάγονται είναι ακέραιες και μεγαλύτερες του μηδενός.

1. ΔΙΑΒΑΣΕ x, y

2. ΑΝ x < y ΤΟΤΕ

3. z

4. ΑΛΛΙΩΣ

5. z <--y

6. ΤΕΛΟΣ_ΑΝ

7. ΟΣΟ z <> 0 ΕΠΑΝΑΛΑΒΕ

8. z <--x MOD y

9. x

10. y <--z

11. ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ

Β1. Να αναπαραστήσετε με διάγραμμα ροής το παραπάνω τμήμα αλγορίθμου.

Β2. Δίνεται το ακόλουθο υπόδειγμα πίνακα τιμών:

αριθμός γραμμής	x	y	z
1	150	35
...	...	...	...
Στη στήλη με τίτλο «αριθμός γραμμής» καταγράφεται ο αριθμός γραμμής της εντολής που εκτελείται. Στη συνέχεια του πίνακα υπάρχει μια στήλη για κάθε μεταβλητή του αλγορίθμου. Να μεταφέρετε τον πίνακα στο τετράδιό σας και να τον συμπληρώσετε, εκτελώντας τις εντολές του τμήματος αλγορίθμου για x = 150 και y = 35 ως εξής: Για κάθε εντολή που εκτελείται να γράψετε σε μία νέα γραμμή του πίνακα τον αριθμό της γραμμής της και το αποτέλεσμα της εκτέλεσης της εντολής. Σημείωση: Στον πίνακα τιμών έχει συμπληρωθεί η εκτέλεση της πρώτης εντολής του αλγορίθμου Β3 Να μετατραπεί η δομή ΟΣΟ... ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ του παραπάνω αλγορίθμου σε ισοδύναμη με τη χρήση της δομής ΑΡΧΗ_ΕΠΑΝΑΛΗΨΗΣ... ΜΕΧΡΙΣ_ΟΤΟΥ

Επαναλ 2009

Δίνεται το παρακάτω τμήμα δηλώσεων ενός προγράμματος σε «ΓΛΩΣΣΑ»:

ΜΕΤΑΒΛΗΤΕΣ

ΑΚΕΡΑΙΕΣ: Χ, Ζ[15]

ΠΡΑΓΜΑΤΙΚΕΣ: Ω

Να μετατρέψετε τις ενέργειες που δίνονται παρακάτω σε εντολές της «ΓΛΩΣΣΑΣ»:

α. Εκχώρησε την τιμή -3 στη μεταβλητή Χ.

β. Εκχώρησε την τιμή της μεταβλητής Χ στις πρώτες πέντε θέσεις του πίνακα Ζ.

γ. Εμφάνισε τις τιμές των δύο πρώτων θέσεων του πίνακα Ζ.

δ. Εκχώρησε στη μεταβλητή Ω τον μέσο όρο των τιμών των δύο τελευταίων θέσεων του πίνακα Ζ.

ε. Αν 1 <= Χ <= 15 εμφάνισε την τιμή της θέσης Χ του πίνακα Ζ.

Απάντηση

α. Χ<-- -3

β. Γιά i από 1 μέχρι 5
Ζ[i]<--X
Τ_Ε

γ. Γιά i από 1 μέχρι 2
Εμφάνισε Ζ[i]
Τ_Ε

δ. Ω<--(Ζ[14]+Ζ[15])/2

ε. Γιά Χ από 1 μέχρι 15
Εμφάνισε Ζ[Χ]
Τ_Ε

***
Δομή επιλογής

Δίνεται το παρακάτω τμήμα αλγορίθμου:

Αν Α>=5 τότε

Αν Β<7 τότε

Α<-- Α+1

αλλιώς

Α<--Α-1

Τέλος_αν

αλλιώς

Α<--Α-1

Τέλος_αν

Εμφάνισε Α

Επίσης δίνονται δίπλα δύο τμήματα αλγορίθμων από τα οποία λείπουν οι συνθήκες:

Να γράψετε στο τετράδιό σας τις συνθήκες που λείπουν, ώστε κάθε ένα από τα τμήματα α, β να εμφανίζει το ίδιο αποτέλεσμα με το αρχικό

α. Αν ................. τότε

Α<-- Α+1

αλλιώς

Α<-- Α-1

Τέλος_αν

ΕμφάνισεΑ

Λύση

η εντολή Α<-- Α+1 εκτελείται όταν Α>=5 και Β<7 ,
η εντολή Α<-- Α-1 εκτελείται όταν (Α<5και Β>=7) , ή όταν Α<--5

οπότε

α. Αν Α>=5 και Β<7 τότε

Α<-- Α+1

αλλιώς

Α< Α-1

Τέλος_αν

Εμφάνισε Α

β. Αν ................. τότε

Α<-- Α-1

αλλιώς

Α<-- Α+1

Τέλος_αν

ΕμφάνισεΑ

Λύση

β. Αν Α<5και Β>=7 τότε

Α<-- Α-1

αλλιώς

Α<-- Α+1

Τέλος_αν

ΕμφάνισεΑ

***
Δομή επιλογής

Να γραφεί πρόγραμμα που θα δέχεται μια τιμή χ και θα υπολογίζει την παράσταση

	χ³ για	-21< χ< -2
	χ/(χ+1) για	-2 < χ< 2
Κ=	ημχ για	2 <χ<= 3
	¦χ¦ για	3 <χ<= 2011

Το πρόγραμμα να γίνει με δύο τρόπους
α. με χρήση της δομής επιλογής Αν.. τότε Αλλιώς Αν... αλλιώς ...Τέλος_αν
β. με χρήση εμφωλευμένων δομών επιλογής

Λύση
α.
...
Διάβασε χ
Αν χ>-21 και χ< -2 τότε
Κ<--χ^3
Αλλιώς_αν χ>-2 και χ<2 και χ<> -1 τότε
Κ<--χ/(χ+1)
Αλλιώς_αν χ> 2 και χ?3 τότε
Κ<--ΗΜ(χ)
Αλλιώς_αν χ> 3 και χ<= 2011 τότε
Κ<--Α_Τ(χ)
Τέλος_Αν
...

αρκεί την εντολή
Αλλιώς_αν ............ τότε να την κάνουμε
Αλλιώς
Αν........τότε

Λύση
β.
...
Διάβασε χ
Αν χ>-21 και χ< -2 τότε
Κ<--χ^3
Αλλιώς
αν χ>-2 και χ<2 και
χ<> -1 τότε
Κ<--χ/(χ+1)
Αλλιώς
αν χ> 2 και χ<=3 τότε
Κ<--ΗΜ(χ)
Αλλιώς
αν χ> 3 και χ? 2011 τότε
Κ<--Α_Τ(χ)
Τέλος_Αν
Τέλος_Αν
Τέλος_Αν
Τέλος_Αν
...

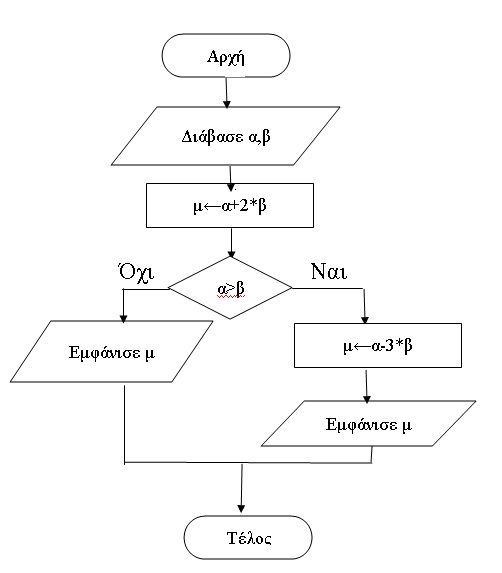
Για το παρακάτω διάγραμμα ροής
α) Να γράψετε τον αντίστοιχο αλγόριθμο με χρήση της σύνθετης επιλογής Αν ...τότε αλλιώς.... Τέλος_Αν
β) Να γράψετε τον αντίστοιχο αλγόριθμο με χρήση της απλής επιλογής Αν ...τότε ... Τέλος_Αν και να κάνετε το αντίστοιχο διάγραμμα ροής

Απάντηση

...
Διάβασε α,β
μ<--α+2*β
Αν α>β τότε
μ<--α-3*β
Εμφάνισε μ
Αλλιώς
Εμφάνισε μ
Τέλος_Αν
...

Διάβασε α,β

μ<--α+2*β

Αν α>β τότε
μ<--α-3*β
Τέλος_Αν
Εμφάνισε μ

Να γράψετε τον Αλγόριθμο σε μορφή κωδικοποίησης

Λύση

Διάβασε α
Αν α>=20 τότε
κ<--12
εμφάνισε ''2011''
Αλλιώς
Αν ΟΧΙ(α>110 και α<=20) τότε
κ<--1
εμφάνισε ''2010-2011''
Τέλος_Αν
Τέλος_Αν
τέλος

Να γράψετε τον Αλγόριθμο σε μορφή κωδικοποίησης

Λύση
Διάβασε α

ΟΣΟ α>=20 ΕΠΑΝΑΛΑΒΕ
κ<--12
Διάβασε α
ΤΕΛΟΣ ΕΠΑΝΑΛΗΨΗΣ
Αν ΟΧΙ(α>110 και α<=20) τότε
κ<--1
εμφάνισε 2010-2011
Τέλος_Αν
τέλος

Δίνονται οι τιμές των μεταβλητών Α=3, Β=1, Γ=15 και η παρακάτω έκφραση:

(ΟΧΙ (Α+Β*3>10)) ΚΑΙ (Γ MOD (A-B)=1)

Nα υπολογίσετε την τιμή της έκφρασης αναλυτικά ως εξής:

α. Να αντικαταστήσετε τις μεταβλητές με τις τιμές τους.

β. Να εκτελέσετε τις αριθμητικές πράξεις.

γ. Να αντικαταστήσετε τις συγκρίσεις με την τιμή ΑΛΗΘΗΣ, αν η σύγκριση είναι αληθής, ή την τιμή ΨΕΥΔΗΣ, αν είναι ψευδής.

δ.Να εκτελέσετε τις λογικές πράξεις, ώστε να υπολογίσετε την τελική τιμή της έκφρασης

Λύση

(ΟΧΙ (3+1*3>10)) ΚΑΙ (15 MOD (3-1)=1)

(ΟΧΙ (6>10)) ΚΑΙ (1=1)

(ΟΧΙ (ΨΕΥΔΗΣ) ΚΑΙ (ΑΛΗΘΗΣ)

(ΑΛΗΘΗΣ) ΚΑΙ (ΑΛΗΘΗΣ) =ΑΛΗΘΗΣ

Επαναλ 2008
Δίνεται το παρακάτω πρόγραμμα σε «ΓΛΩΣΣΑ»

1. ΠΡΟΓΡΑΜΜΑ ΕΙΝΑΙ-ΠΡΩΤΟΣ

2. ΜΕΤΑΒΛΗΤΕΣ

3. ΑΚΕΡΑΙΕΣ: Χ, i

4. ΧΑΡΑΚΤΗΡΕΣ: ΜΗΝΥΜΑ

5. ΑΡΧΗ

6. ΑΡΧΗ_ΕΠΑΝΑΛΗΨΗΣ

7. ΔΙΑΒΑΣΕ Χ

8. ΜΕΧΡΙΣ_ΟΤΟΥ Χ>0

9. C<--0

10. ΓΙΑ i ΑΠΟ 1 ΜΕΧΡΙ Χ ΕΠΑΝΑΛΑΒΕ

11. AN (Χ MOD i) = 0 TOTE

12. C <--C + 1

13. ΤΕΛΟΣ_ΑΝ

14. ΤΕΛΟΣ_ΓΙΑ

15. ΑΝ C=2 TOTE

16. MHNYMA <-- ‘EINAI ΠΡΩΤΟΣ’

17. ΑΛΛΙΩΣ

18. ΜΗΝΥΜΑ <-- ‘ΔΕΝ ΕΙΝΑΙ ΠΡΩΤΟΣ’

19. ΤΕΛΟΣ

20. ΓΡΑΨΕ ΜΗΝΥΜΑ

21. ΤΕΛΟΣ_ΑΛΓΟΡΙΘΜΟΥ

Να γράψετε στο τετράδιό σας τον αριθμό κάθε γραμμής του προγράμματος, στην οποία εντοπίζετε συντακτικό λάθος και να περιγράψετε το λάθος αυτό.

Δίνεται το παρακάτω τμήμα αλγορίθμου

ΑΝ π <= 50 TOTE

Κόστος <--π * 580

ΑΛΛΙΩΣ_ΑΝ π > 50 ΚΑΙ π<= 100 ΤΟΤΕ

Κόστος <--π* 520

ΤΕΛΟΣ 1ΗΣ ΣΕΛΙΔΑΣ ΑΡΧΗ 2ΗΣ ΣΕΛΙΔΑΣ

ΑΛΛΙΩΣ_ΑΝ π> 100 ΚΑΙ π<= 200 ΤΟΤΕ

Κόστος<--π* 470

ΑΛΛΙΩΣ

Κόστος <-- π* 440

ΤΕΛΟΣ_ΑΝ

Στο παραπάνω τμήμα αλγορίθμου, για το οποίο θεωρούμε ότι το π είναι θετικός αριθμός, περιλαμβάνονται περιττοί έλεγχοι.

Να το ξαναγράψετε παραλείποντας τους περιττούς ελέγχους.

Παρατηρήσεις

1. τα χρωματισμένα είναι απλά περιττά αλλά όχι λάθος

2. Αν η άσκηση ξεκινά με
ΑΝ π>23 και π<= 50
τότε θα ήταν λάθος να τους παραλείψουμε
Γενικά για να παραλείψω περιττούς ελέγχους πρέπει η μεταβλητή να καλύπτει όλο το πεδίο ορισμού της

Δίνεται η παρακάτω ακολουθία αριθμών: 25, 8, 12, 14, 71, 41, 1. Τοποθετούμε τους αριθμούς σε στοίβα και σε ουρά.

1. Ποια λειτουργία θα χρησιμοποιηθεί για την τοποθέτηση των αριθμών στη στοίβα και ποια για την τοποθέτησή τους στην ουρά;

2. Να σχεδιάσετε τις δύο δομές (στοίβα και ουρά) μετά την τοποθέτηση των αριθμών.

3. Ποια λειτουργία θα χρησιμοποιηθεί για την έξοδο αριθμών από τη στοίβα και ποια για την έξοδό τους από την ουρά;

4. Πόσες φορές θα πρέπει να γίνει η παραπάνω λειτουργία στη στοίβα και πόσες στην ουρά για να εξέλθει ο αριθμός 71;

Απάντηση
1 Στοίβα ώθηση Ουρά εισαγωγή

<--

3 Στοίβα απώθηση Ουρά εξαγωγή

4 Στοίβα τρείς φορές Ουρά 5 φορές

Επαναλ 2005

Δίνεται το παρακάτω πρόγραμμα το οποίο διαβάζει τις

θερμοκρασίες διαφόρων ημερών του μήνα, έστω 30, και

υπολογίζει τη μέση θερμοκρασία του μήνα.

ΠΡΟΓΡΑΜΜΑ Θερμοκρασίες

ΜΕΤΑΒΛΗΤΕΣ

ΠΡΑΓΜΑΤΙΚΕΣ: Θερμοκρασία [30], Μέση, Σύνολο

ΑΚΕΡΑΙΕΣ: i

ΑΡΧΗ

Σύνολο <--0

ΓΙΑ i ΑΠΟ 1 ΜΕΧΡΙ 30

ΓΡΑΨΕ ''Δώσε τη θερμοκρασία''

ΔΙΑΒΑΣΕ Θερμοκρασία [i]

Σύνολο <-- Σύνολο + Θερμοκρασία [i]

ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ

Μέση <-- Σύνολο/30

ΓΡΑΨΕ “Μέση Θερμοκρασία:”, Μέση

ΤΕΛΟΣ_ΠΡΟΓΡΑΜΜΑΤΟΣ

α) Να γραφεί αντίστοιχο πρόγραμμα (που να κάνει τους

ίδιους υπολογισμούς) χωρίς τη χρήση πίνακα.

β) Έστω ότι οι τιμές των θερμοκρασιών έχουν δοθεί στην

κλίμακα Κελσίου. Να τροποποιηθεί το πρόγραμμα που

δόθηκε έτσι, ώστε κάνοντας χρήση συνάρτησης να

μετατρέπονται οι θερμοκρασίες από την κλίμακα

Κελσίου σε κλίμακα Φαρενάιτ.

Ο τύπος μετατροπής από Κελσίου σε Φαρενάιτ είναι:

Φαρενάιτ=32+(9.Κελσίου)/5

Να γραφεί τόσο το υποπρόγραμμα της συνάρτησης όσο και η κλήση της στο κύριο πρόγραμμα

ΘΕΜΑ 2ο ΕΠΑΝΑΛ 2004

Δίνεται ο παρακάτω αλγόριθμος:

Αλγόριθμος Αριθμοί_ ΜΕΡΣΕΝ

Διάβασε Α

Β <-- 4

C <--2

Aρχή_επανάληψης

Β (Β^2) – 2

Εμφάνισε Β

C <-- C + 1

Μέχρις_ότου C > (A – 1)

D <-- (2^A) – 1

E <-- B MOD D

Εμφάνισε D

Αν E = 0 τότε

F <-- (2^(C – 1)) * D

Εμφάνισε "Τέλειος αριθμός:", F

G <-- 0

Όσο F > 0 επανάλαβε

G <-- G + 1

F <-- F DIV 10

Τέλος_επανάληψης

Εμφάνισε G

Τέλος_αν

Τέλος Αριθμοί_ΜΕΡΣΕΝ

Να γράψετε στο τετράδιό σας τις τιμές που τυπώνει ο

παραπάνω αλγόριθμος, αν του δώσουμε τιμές εισόδου:

α. 3 β. 4

Δίνεται η παρακάτω αλληλουχία εντολών:

Διάβασε α, β

Αν α > β τότε

c <-- α/ (β- 2)

Τέλος_αν

Εκτύπωσε c

α. Να απαντήσετε στο τετράδιό σας με Ναι ή Όχι αν η παραπάνω Αλληλουχία εντολών ικανοποιεί όλα τα αλγοριθμικά κριτήρια.

β. Να αιτιολογήσετε την απάντησή σας.

Καθοριστικότητα:
μπορεί β=2

Δίνεται η παρακάτω αλληλουχία εντολών:

α 1

Όσο α<> 6 επανάλαβε

α α+ 2

Τέλος_επανάληψης

Εκτύπωσε α

α. Να απαντήσετε στο τετράδιό σας με Ναι ή Όχι αν η παραπάνω αλληλουχία εντολών ικανοποιεί όλα τα αλγοριθμικά κριτήρια.

β. Να αιτιολογήσετε την απάντησή σας.

Περατότητα