Αρχική ΑΕΠΠ - Δομές Δεδομένων Λειτουργικά Συστήματα Δίκτυα Υπολογιστών ΙΙ Βάσεις Δεδομένων Παιδαγωγικά - Διδακτική
Βασικές Έννοιες
Μεταβλητή - Έκφραση Δομή Ακολουθίας Δομή Επιλογής Δομή Επανάληψης
Αναπαράσταση Αλγορίθμων
Πίνακες
Μονοδιάστατοι Δισδιάστατοι Πολυδιάστατοι Αναζήτηση Ταξινόμηση Στοίβα Ουρά
Υποπρογράμματα
Συναρτήσεις Διαδικασίες Σχετικά με τις παράμετρους
Δυναμικές Δομές
AVL Δέντρα (Ισορροπημένα)
Ένα δέντρο AVL είναι ένας ειδικός τύπος δυαδικού δέντρου που είναι πάντα "μερικώς" ισορροπημένο. Το κριτήριο που χρησιμοποιείται για να καθορίσει το βαθμό ισορροπίας είναι η διαφορά μεταξύ των υψών των υποδέντρων κάθε κόμβου. Το κριτήριο, λοιπόν, ισορροπίας είναι το ακόλουθο:
Τη διαφορά αυτή, εδώ, τη συμβολίζουμε με:
B(x)=HR-HL
HR το ύψος του δεξιού υποδέντρου του κόμβου, και
HL το ύψος του αριστερού υποδέντρου
Η τιμή αυτή μπορεί να είναι -1, 0 ή 1. Τιμή -1 σημαίνει ότι το αριστερό υποδέντρο έχει μεγαλύτερο ύψος από το δεξί, η τιμή 0 ότι τα δύο υποδέντρα έχουν το ίδιο ύψος και η τιμή 1 ότι το δεξί υποδέντρο έχει μεγαλύτερο ύψος.
Αν η ισορροπία ενός κόμβου γίνει -2 ή 2, αυτό σημαίνει ότι ο κόμβος χρειάζεται εξισορρόπηση. Αυτό επιτυγχάνεται κάνοντας τις κατάλληλες περιστροφές.
Η εισαγωγή/διαγραφή κόμβων γίνεται όπως στα δυαδικά δέντρα. Αν η ενέργεια διαταράξει την ισορροπία κόμβων πρέπει αυτή να αποκατασταθεί. Η αποκατάσταση γίνεται κάνοντας περιστροφή των κόμβων των οποίων η ισορροπία διαταράχθηκε. Πριν δούμε, λοιπόν, την εισαγωγή και τη διαγραφή, θα δούμε πρώτα τις δυνατές περιστροφές.
Περιστροφές
Απλή Αριστερή Περιστροφή (LL)
Έχουμε το παρακάτω τμήμα ενός δέντρου.
a B(a)=1-0 => B(a)=1 \ b B(b)=0
Σχήμα 1
Αν γίνει εισαγωγή κόμβου ως δεξί παιδί του b, το δέντρο γίνεται:
a B(a)=2-0 => B(a)=2
\
b B(b)=1-0 => B(c)=1
\
c B(c)=0
Έχουμε διαταραχή της ισορροπίας για τον κόμβο a η οποία λύνεται με τα παρακάτω βήματα:
- Ο κόμβος
bγίνεται η νέα ρίζα - Το αριστερό παιδί του κόμβου
bγίνεται δεξί παιδί του κόμβουa
Σε αυτή την περίπτωση δεν υπάρχει αριστερό παιδί στονb - Ο κόμβος
aγίνεται αριστερό παιδί του κόμβουb
Έτσι, το δέντρο γίνεται:
b B(b)=1-1 => B(b)=0 / \ a c B(a)=0, B(b)=0
Γενικεύοντας την περίπτωση, μπορούμε να πούμε ότι απλή αριστερή περιστροφή έχουμε όταν η ισορροπία του "παππού" του νέου κόμβου (c στο παράδειγμα), γίνει 2 και η ισορροπία του "πατέρα" του νέου κόμβου γίνει 1.
Σε περίπτωση που η εισαγωγή κόμβου στο σχήμα 1 γίνει αριστερό παιδί του b, τότε έχουμε την περίπτωση της Αριστερής - Δεξιάς Περιστροφής.
Απλή Δεξιά Περιστροφή (RR)
Ας, υποθέσουμε ότι έχουμε το παρακάτω τμήμα ενός δέντρου.
c B(c)=0-1 => B(c)=-1
/
b B(b)=0
Σχήμα 2
Αν γίνει εισαγωγή κόμβου ως αριστερό παιδί του κόμβου b, έχουμε το παρακάτω δέντρο.
c B(c)=0-2 => B(c)=-2
/
b B(b)=0-1 => B(b)=-1
/
a B(a)=0
Έχουμε διαταραχή της ισορροπίας για τον κόμβο c η οποία λύνεται με τα παρακάτω βήματα
- Ο κόμβος
bγίνεται η νέα ρίζα - Το δεξί παιδί του κόμβου
bγίνεται αριστερό παιδί του κόμβουc
Σε αυτή την περίπτωση δεν έχουμε αριστερό παιδί του κόμβουb - Ο κόμβος
cγίνεται δεξί παιδί του κόμβουb
Έτσι, το δέντρο γίνεται:
b B(b)=1-1 => B(b)=0 / \ a c B(a)=0, B(c)=0
Γενικεύοντας και εδώ την περίπτωση, μπορούμε να πούμε ότι απλή δεξιά περιστροφή έχουμε όταν η ισορροπία του "παππού" του νέου κόμβου (c στο παράδειγμα), γίνει -2 και η ισορροπία του "πατέρα" του νέου κόμβου γίνει -1.
Σε περίπτωση που η εισαγωγή κόμβου στο σχήμα 2 γίνει δεξί παιδί του b, τότε έχουμε την περίπτωση της Δεξιάς - Αριστερής Περιστροφής.
Αριστερή - Δεξιά Περιστροφή (ή "Διπλή Αριστερή")
Μερικές φορές η απλή αριστερή περιστροφή δεν είναι αρκετή για να αποκαταστήσει την ισορροπία του δέντρου. Ας δούμε την παρακάτω περίπτωση.
a Β(a)=1-0 => B(a)=1 \ c B(c)=0
Σχήμα 3
Το δέντρο είναι ισορροπημένο. Η εισαγωγή ενός κόμβου ως δεξί παιδιού του κόμβου c οδηγεί στην περίπτωση της απλής αριστερής περιστροφής. Τι γίνεται όμως με εισαγωγή ενός κόμβου που θα γίνει αριστερό παιδί του c. Σ' αυτή την περίπτωση έχουμε το παρακάτω σχήμα.
a Β(a)=2-0 => B(a)=2 \ c B(c)=0-1 => B(c)=-1 / b
Αυτό το δέντρο δεν είναι ισορροπημένο. Η ισορροπία του a ("παππού" του b) είναι θετική και ίση με 2. Αν δοκιμάσουμε να κάνουμε μία απλή αριστερή περιστροφή, ακολουθούμε τα γνωστά βήματα και:
- Ο κόμβος
cγίνεται η νέα ρίζα - Το αριστερό παιδί του κόμβου
cγίνεται δεξί παιδί του κόμβουa - Ο κόμβος
aγίνεται αριστερό παιδί του κόμβουc
Έτσι, το δέντρο γίνεται:
c B(c)=0-2 => B(c)=-2 / a B(a)=1-0 => B(a)=1 \ b B(b)=0
Βλέπουμε ότι η περιστροφή δεν έλυσε το πρόβλημα. Μία προσπάθεια απλής δεξιάς περιστροφής (ισορροπία "παππού" -2) δε θα λύσει πάλι το πρόβλημα. Θα φτάσουμε στην προηγούμενη κατάσταση.
Η διαδικασία που ακολουθούμε σε αυτή την περίπτωση είναι η εξής:
- Κάνουμε απλή δεξιά περιστροφή στο υποδέντρο με ρίζα τον κόμβο
c
a Β(a)=2-0 => B(a)=2
\
b B(c)=1-0 => B(c)=1
\
c B(c)=0
Βλέπουμε ότι έχουμε B(a)=2 και B(b)=1, άρα, αυτό που έχουμε είναι να
- Κάνουμε απλή αριστερή περιστροφή στο δέντρο με ρίζα τον κόμβο
a
b B(b)=1-1 => B(b)=0 / \ a c B(a)=0, B(c)=0
Βλέπουμε ότι αυτή η διαδικασία αποκαθιστά την ισορροπία. Γενικεύοντας την περίπτωση, αν η ισορροπία του "παππού" του νέου κόμβου είναι 2 και η ισορροπία του "πατέρα" είναι -1, τότε κάνουμε Αριστερή-Δεξιά Περιστροφή.
Δεξιά - Αριστερή Περιστροφή (ή "Διπλή Δεξιά")
Αυτή η περίπτωση είναι όμοια με την Αριστερή - Δεξιά Περιστροφή με την έννοια ότι είναι συμμετρική της. Ας δούμε την παρακάτω περίπτωση.
c Β(c)=0-1 => B(c)=-1 / a B(a)=0
Σχήμα 4
Το δέντρο είναι ισορροπημένο. Η εισαγωγή ενός κόμβου ως αριστρερού παιδιού του κόμβου a οδηγεί στην περίπτωση της απλής δεξιάς περιστροφής. Με την εισαγωγή ενός κόμβου που θα γίνει δεξί παιδί του a, έχουμε το παρακάτω σχήμα.
c B(c)=0-2 => B(c)=-2 / a B(a)=1-0 => B(a)=1 \ b B(b)=0
Αυτό το δέντρο δεν είναι ισορροπημένο. Η ισορροπία του c ("παππού" του b) είναι αρνητική και ίση με -2. Αν δοκιμάσουμε να κάνουμε μία απλή δεξιά περιστροφή, ακολουθούμε τα γνωστά βήματα και:
- Ο κόμβος
aγίνεται η νέα ρίζα - Το δεξί παιδί του κόμβου
aγίνεται αριστερό παιδί του κόμβουc - Ο κόμβος
cγίνεται δεξί παιδί του κόμβουa
Έτσι, το δέντρο γίνεται:
a B(a)=2-0 => B(c)=2
\
c B(a)=0-1 => B(a)=-1
/
b B(b)=0
Βλέπουμε πάλι ότι η περιστροφή δεν έλυσε το πρόβλημα. Επίσης, μία προσπάθεια απλής αριστερής περιστροφής (ισορροπία "παππού" 2) δε θα λύσει πάλι το πρόβλημα. Θα φτάσουμε στην προηγούμενη κατάσταση.
Η διαδικασία που ακολουθούμε σε αυτή την περίπτωση είναι η εξής:
- Κάνουμε απλή αριστερή περιστροφή στο υποδέντρο με ρίζα τον κόμβο
a
c Β(c)=0-2 => B(a)=-2
/
b B(b)=0-1 => B(b)=-1
/
a B(a)=0
Βλέπουμε ότι έχουμε B(c)=-2 και B(b)=-1, άρα, αυτό που έχουμε είναι να
- Κάνουμε απλή δεξιά περιστροφή στο δέντρο με ρίζα τον κόμβο
c
b B(b)=1-1 => B(b)=0 / \ a c B(a)=0, B(c)=0
Βλέπουμε ότι αυτή η διαδικασία αποκαθιστά την ισορροπία. Γενικεύοντας την περίπτωση, αν η ισορροπία του "παππού" του νέου κόμβου είναι -2 και η ισορροπία του "πατέρα" είναι 1, τότε κάνουμε Δεξιά - Αριστερή Περιστροφή.
Ανακεφαλαίωση
Συγκεντρώνοντας τις παραπάνω παρατηρήσεις, δημιουργούμε τον παρακάτω πίνακα αποφάσεων.
| Ισορροπία | Περιστροφή | |
|---|---|---|
| Παππού | Πατέρα | |
| 2 | 1 ή 0 | Απλή Αριστερή |
| 2 | -1 ή 0 | Αριστερή - Δεξιά |
| -2 | -1 ή 0 | Απλή Δεξιά |
| -2 | 1 ή 0 | Δεξιά - Αριστερή |
Στην πραγματικότητα οι περιστροφές είναι δύο. Οι άλλες δύο είναι συμμετρικές αυτών. Αν πάρουμε για παράδειγμα τις δεξιές περιστροφές, τότε έχουμε
- απλή δεξιά με συμμετρική την απλή αριστερή
- δεξιά - αριστερή με συμμετρική την αριστερή - δεξιά

(α) Αρχική κατάσταση σε ισορροπία
Τα υποδέντρα 1 και 2 του κόμβου Α έχουν ύψος h. Το αριστερό υποδέντρο του κόμβου Β έχει ύψος 1+h. Το ένα προκύπτει από τον κόμβο Α. Έτσι, έχουμε:
HL=h+1
Το ύψος του δεξιού υποδέντρου του κόμβου Β είναι h. Δηλαδή:
HR=h
Η ισορροπία του κόμβου Β είναι:
Β(Β)=HR-HL=h-(h+1) => B(B)=-1
(β) Γίνεται εισαγωγή του κόμβου Χ
Η εισαγωγή γίνεται ως παιδί του υποδέντρου 1 του κόμβου Α. Αν γίνει εισαγωγή στο υποδέντρο 2, τότε έχουμε την περίπτωση 2.
Στο παραπάνω σχήμα φαίνεται ότι η ισορροπία του κόμβου Β γίνεται -2 και του Α γίνεται -1. Για την αποκατάσταση της ισορροπίας χρειάζεται μία απλή δεξιά περιστροφή.
(γ) Αποκατάσταση της ισορροπίας
Ακολουθώντας τα βήματα έχουμε:
- Ο κόμβος
Απαίρνει τη θέση του κόμβουΒ - Το υποδέντρο
2γίνεται υποδέντρο του κόμβουΒ(από αριστερό τουΑγίνεται δεξί τουΒ) - Ο κόμβος
Βγίνεται δεξί υποδέντρο του κόμβουΒ
(α) Αρχική κατάσταση
Τα υποδέντρα 1, 2 και 3 έχουν ύψος h. Το υποδέντρο 4 έχει ύψος 2h. Αυτό δίνει τιμή ισορροπίας στον κόμβο C -1 και στον κόμβο Α 1. Ο κόμβος Β έχει τιμή 0.
Β(C)=HR+HL=2h-(1+2h) => B(C)=-1
B(A)=HR+HL=(1+h)-h => B(A)=1
(β) Εισαγωγή του κόμβου Χ
Η εισαγωγή του κόμβου Χ μπορεί να γίνει στο υποδέντρο 2 ή 3. Σε όποιο και να γίνει η διαδικασία είναι ίδια.
Οι τιμές στους κόμβους γίνονται:
B(C)=2h-(1+2h+1) => B(C)=-2
B(A)=(1+h+1)-h => B(A)=2
B(B)=-1 (αν η εισαγωγή γίνει στο υποδέντρο 2) ή Β(Β)=1 (αν γίνει στο 3)
(γ) Αποκατάσταση της ισορροπίας
Τα βήματα που αποκαταστούν την ισορροπία είναι αυτά της δεξιάς - αριστερής περιστροφής. Εδώ μπορούμε να συνοψίσουμε λίγο τα βήματα αυτά, οπότε έχουμε:
- Ο κόμβος
Βπαίρνει τη θέση του κόμβουC - Ο κόμβος
Cγίνεται δεξί παιδί του κόμβουΒ - Το υποδέντρο
2γίνεται δεξί παιδί του κόμβουΑ - Το υποδέντρο
3γίνεται αριστερό παιδί του κόμβουC
Εισαγωγή Κόμβων
Η εισαγωγή του κόμβου γίνεται όπως και στην περίπτωση των δυαδικών δέντρων. Αφού γίνει η εισαγωγή του κόμβου, προχωρούμε προς τα πίσω στους κόμβους από τους οποίους περάσαμε και σε κάθε κόμβο υπολογίζουμε το βαθμό ισορροπία του. Αν έχει διαταραχθεί, κάνουμε τις κατάλληλες περιστροφές.
Η διαδικασία θα γίνει πιο κατανοητή με ένα παράδειγμα.
Παράδειγμα
Ας υποθέσουμε ότι έχουμε με τη σειρά τους αριθμούς: 4, 5, 7, 2, 1, 3, 6
- Εισαγωγή
4

- Εισαγωγή
5

- Εισαγωγή
7

Εδώ βλέπουμε ότι ο κόμβος 4 έχει τιμή 2 και ο κόμβος 5 1. Κάνουμε, λοιπόν, μία απλή αριστερή περιστροφή για τους κόμβους 4, 5, 7. Έχουμε:
- ο κόμβος
5γίνεται ρίζα στην θέση του4 - ο κόμβος
4γίνεται αριστερό παιδί του κόμβου5
Έτσι, το δέντρο γίνεται:

- Εισαγωγή
2

- Εισαγωγή
1

Με αυτή την εισαγωγή, ο κόμβος 4 έχει τιμή -2 και ο κόμβος 2 -1. Κάνουμε, απλή δεξιά περιστροφή στους κόμβους 4, 2, 1. Έχουμε:
- ο κόμβος
2παίρνει τη θέση του κόμβου4 - ο κόμβος
4γίνεται δεξί παιδί του κόμβου2
Το δέντρο γίνεται:

- Εισαγωγή
3

Με την εισαγωγή του κόμβου 3, ο κόμβος 5 αποκτά τιμή -2 και ο 2 τιμή 1. Για να αποκαταστήσουμε την ισορροπία πρέπει να κάνουμε μία δεξιά - αριστερή περιστροφή στους κόμβους 5, 2, 4.
Πρώτα κάνουμε την αριστερή περιστροφή στους κόμβου 2 και 4.
- ο κόμβος
4γίνεται ρίζα στη θέση του2 - το αριστερό παιδί του κόμβου
4γίνεται δεξί παιδί του κόμβου2 - ο κόμβος
2γίνεται αριστερό παιδί του κόμβου4
Το δέντρο γίνεται:

Τώρα κάνουμε την δεξιά περιστροφή:
- ο κόμβος
4γίνεται ρίζα, στη θέση του5 - ο κόμβος
5γίνεται δεξί παιδί στον κόμβο4
Τώρα το δέντρο γίνεται:

- Εισαγωγή
6
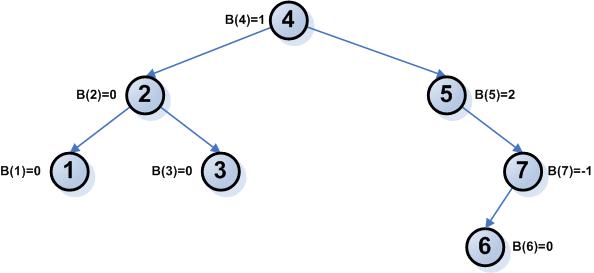
Ο κόμβος 5 έχει τιμή 2 και ο 7 τιμή -1. Για την αποκατάσταση της ισορροπίας πρέπει να κάνουμε μία αριστερή - δεξιά περιστροφή.
Πρώτα κάνουμε δεξιά περιστροφή στους κόμβους 7 και 6.
- ο κόμβος
6γίνεται ρίζα στη θέση του κόμβου7 - ο κόμβος
7γίνεται δεξί παιδί του κόμβου6
Το δέντρο γίνεται:

Τώρα κάνουμε αριστερή περιστροφή στους κόμβους 5, 6 και 7.
- ο κόμβος
6γίνεται ρίζα στη θέση του κόμβου5 - ο κόμβος
5γίνεται αριστερό παιδί του κόμβου6.
Το δέντρο γίνεται:
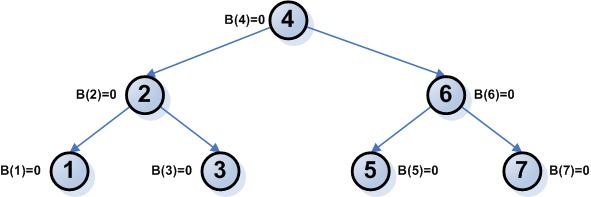
Διαγραφή Κόμβων
Η διαγραφή κόμβων δεν είναι πιο δύσκολη από την εισαγωγή, εκτός από μία περίπτωση όπου απλά πρέπει να προσέξουμε ποιος κόμβος πρέπει να πάρει τη θέση εκείνου που διαγράφηκε. Σε κάθε διαγραφή κόμβου, πρέπει όπως και στην εισαγωγή, να διασχίσουμε το μονοπάτι από τον κόμβο που αντικαθιστά τον διαγραμμένο προς τη ρίζα και να υπολογίσουμε την ισορροπία των κόμβων. Αν βρούμε διαταραχές, τις αντιμετωπίζουμε με τις γνωστές περιστροφές.
Οι βασικές περιπτώσεις διαγραφής κόμβων είναι:
- Ο κόμβος που διαγράφεται είναι τερματικός (δεν έχει παιδιά)
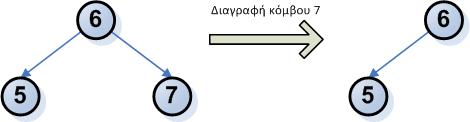
- Ο κόμβος έχει ένα παιδί

- Ο κόμβος έχει δύο παιδιά

- Ο κόμβος έχει υποδέντρα

6. Ο αριστερός του κόμβος είναι ο 3. Από αυτόν τον κόμβο κατεβαίνουμε προς τα δεξιά μέχρι να βρούμε έναν τερματικό κόμβο (που δεν έχει παιδιά) ή να βρούμε έναν κόμβο που έχει μόνο αριστερό παιδί. Σ' αυτό το παράδειγμα βρίσκουμε τον κόμβο 5 ο οποίος παίρνει τη θέση του κόμβου 6.

5. Κατεβαίνουμε στο πρώτο παιδί αριστερά, δηλαδή στον 3. Από τον 3 πρέπει να κατέβουμε δεξιά. Ο κόμβος όμως δεν έχει δεξί παιδί, άρα θα είναι αυτός που θα πάει στη θέση του 5.
Παράδειγμα
Έστω ότι έχουμε το παρακάτω δέντρο στο οποίο γίνονται διαδοχικά διαγραφές των κόμβων 35, 96, 53, 21, 25, 52.

- Διαγραφή 35

- Διαγραφή 96
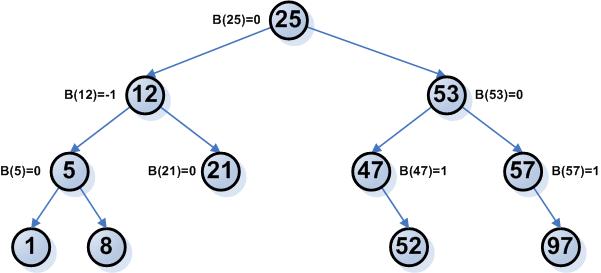
- Διαγραφή 53
52 ο οποίος είναι ο πιο δεξιός κόμβος του αριστερού υποδέντρου.

- Διαγραφή 21
12. Για να αποκατασταθεί η ισορροπία του πρέπει να γίνει απλή δεξιά περιστροφή. Έτσι,
- Ο κόμβος
5γίνεται ρίζα - Ο κόμβος
12γίνεται δεξί παιδί του5 - Ο κόμβος
8γίνεται αριστερό παιδί του5
Το δέντρο, μετά την περιστροφή είναι το παρακάτω.

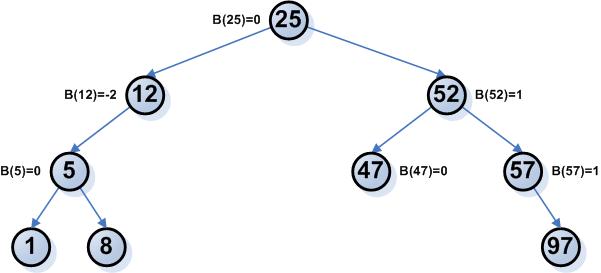
- Διαγραφή 25
25 έχει δύο υποδέντρα. Αντικαθίσταται από το πιο δεξιό παιδί του αριστερού υποδέντρου του, το οποίο είναι το 12.

- Διαγραφή 52
52 έχει δύο υποδέντρα. Αντικαθίσταται από το πιο δεξιό παιδί του αριστερού υποδέντρου του, το οποίο είναι το 47.
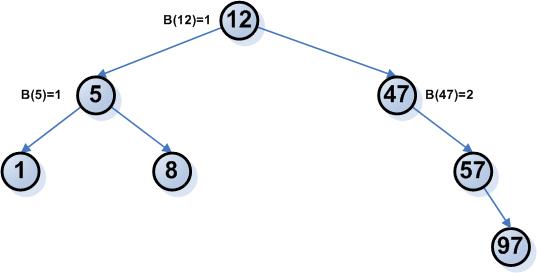
47 δεν είναι ισορροπημένο. Η ισορροπία μπορεί να αποκατασταθεί με μία απλή αριστερή περιστροφή. Έτσι, το δέντρο γίνεται:

Σύνδεσμοι
http://webpages.ull.es/users/jriera/Docencia/AVL/AVL%20tree%20applet.htm
Πάρα πολύ καλό applet για τη δημιουργία δέντρων
- Splay
- Red - Black
- AVL
Προσομοιώνει τις διαδικασίες εισαγωγής, διαγραφής και αναζήτησης.
http://people.ksp.sk/~kuko/bak/
Applet για την προσομοίωση όλων των τύπων δυαδικών δέντρων!
Copyright 2008 - Άρης Φεργάδης
