Αρχική ΑΕΠΠ - Δομές Δεδομένων Λειτουργικά Συστήματα Δίκτυα Υπολογιστών ΙΙ Βάσεις Δεδομένων Παιδαγωγικά - Διδακτική
Βασικές Έννοιες
Μεταβλητή - Έκφραση Δομή Ακολουθίας Δομή Επιλογής Δομή Επανάληψης
Αναπαράσταση Αλγορίθμων
Πίνακες
Μονοδιάστατοι Δισδιάστατοι Πολυδιάστατοι Αναζήτηση Ταξινόμηση Στοίβα Ουρά
Υποπρογράμματα
Συναρτήσεις Διαδικασίες Σχετικά με τις παράμετρους
Δυναμικές Δομές
Βελτίωση Αλγόριθμου Bubble Sort
Ο αλγόριθμος ταξινόμησης με ευθεία ανταλλαγή (bubble sort) μπορεί να βελτιωθεί αν ο αλγόριθμος απομνημονεύει της θέση της τελευταίας ανταλλαγής. Τα στοιχεία του πίνακα μετά τη θέση αυτή είναι σωστά ταξινομημένα, άρα είναι περιττό να ελεγχθούν στα επόμενα περάσματα.
Στο παρακάτω παράδειγμα η ταξινόμηση είναι αύξουσα και η προσπέλαση γίνεται από τα αριστερά προς τα δεξιά. Έστω ο πίνακας με τα στοιχεία:[31, 63, 45, 14, 56, 71, 84, 91]
Με το πρώτο πέρασμα το 63 θα μετακινηθεί στη θέση 5.[31, 45, 14, 56, 63, 71, 84, 91]
Στο επόμενο πέρασμα ο έλεγχος αρκεί να γίνει μέχρι τη θέση 4 γιατί τα στοιχεία πάνω από αυτή είναι ήδη ταξινομημένα.
Γράψτε τον αλγόριθμο ώστε να αξιοποιεί την παραπάνω παρατήρηση.
Αλγόριθμος Ταξινόμησης Shake Sort
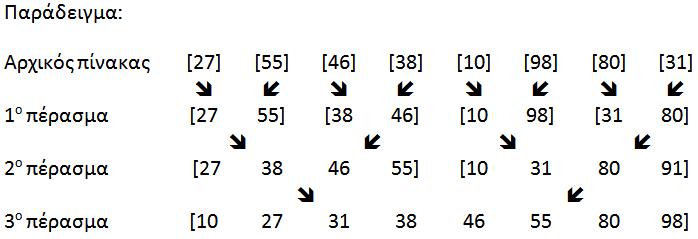
Με τον αλγόριθμο ταξινόμησης με ευθεία ανταλλαγή (bubble sort) μπορούμε να προσπελάσουμε τον πίνακα είτε από πάνω προς τα κάτω, είτε από κάτω προς τα πάνω. Δεχόμενοι ότι κάνουμε αύξουσα ταξινόμηση παρατηρούμε τα εξής: Αν η προσπέλαση γίνεται από πάνω προς τα κάτω, τα μεγάλα νούμερα μετακινούνται στο κάτω άκρο του πίνακα κάνοντας μεγάλα άλματα (αν το μεγαλύτερο στοιχείο ήταν στην πρώτη θέση θα βρεθεί στην τελευταία). Αντιθέτως τα μικρά στοιχεία μετακινούνται μόνο κατά μία θέση πάνω. Ακριβώς τα αντίθετα συμβαίνουν αν η προσπέλαση γίνεται από κάτω προς τα πάνω. Η ασυμμετρία αυτή υποδεικνύει μία ακόμη βελτίωση του αλγορίθμου κατά την οποία τα περάσματα εναλλάσσονται σε διεύθυνση. Ο σχετικός αλγόριθμος αποκαλείται Shake Sort. Να γράψετε τον αλγόριθμο. Ένα παράδειγμα δίνεται παρακάτω.

Δυαδική Παρεμβολή
Στον αλγόριθμο ταξινόμησης με ευθεία παρεμβολή η ακολουθία προορισμού Α[1..i-1] για το i-οστό στοιχείο του πίνακα Α, είναι ταξινομημένη. Μπορεί, λοιπόν, να χρησιμοποιηθεί η μέθοδος της δυαδικής αναζήτησης για την εύρεση της θέση του στοιχείου στην ακολουθία προορισμού. Να υλοποιήσετε τον αυτό τον αλγόριθμο.
Αλγόριθμος Ταξινόμησης Merge Sort
Η τεχνική της συγχώνευσης μπορεί να χρησιμοποιηθεί και για την ταξινόμηση ενός πίνακα. Να γραφεί πρόγραμμα το οποίο θα ταξινομεί ως εξής. Ο αρχικός πίνακας διαιρείται σε N div 2 υποπίνακες. Κάθε υποπίνακας θα έχει δύο στοιχεία και ταξινομείται με απλή εναλλαγή αν χρειάζεται. Στη συνέχεια γίνεται συγχώνευση των υποπινάκων ανά 2 και λαμβάνονται έτσι Ν div 4 ταξινομημένοι υποπίνακες. Η διαδικασία αυτή επαναλαμβάνεται μέχρις ότου ληφθεί ένας πίνακας μεγέθους Ν. Ο αλγόριθμος αυτός ονομάζεται ταξινόμηση με συγχώνευση (merge sort). Θεωρείστε ότι ο πίνακας έχει άρτιο αριθμό στοιχείων.
Αλγόριθμος Ταξινόμησης Shell Sort
Αλγόριθμος Ταξινόμησης Quick Sort
Copyright 2008 - Άρης Φεργάδης