4.1 ΠΟΛΥΠΛΕΚΤΕΣ
4.1.1 ΟΡΙΣΜΟΙ
Ο Πολυπλέκτης (Multiplexer - MUX) 2n εισόδων (2nx1) είναι ένα συνδυαστικό κύκλωμα που έχει n γραμμές επιλογής (ελέγχου) και μία μοναδική γραμμή εξόδου. Το κύκλωμα επιλέγει δυαδικές πληροφορίες από 2n γραμμές εισόδου, ανάλογα με τις τιμές των n γραμμών επιλογής και τις κατευθύνει στην γραμμή εξόδου. Ο συμβολισμός 2nx1 σημαίνει ότι ο πολυπλέκτης έχει 2n εισόδους και μία έξοδο.
Πολύπλεξη (Multiplexing) είναι η επιλογή μίας γραμμής εισόδου δεδομένων από πολλές. Αυτή την λειτουργία την υλοποιούμε με τους Πολυπλέκτες που για αυτό το λόγο ονομάζονται και επιλογείς δεδομένων (data selectors).
Η κύρια εφαρμογή του Πολυπλέκτη είναι η επιλογή μίας από τις πολλές πληροφορίες που εφαρμόζονται στις εισόδους του και η μεταφορά της στην έξοδό του.
4.1.2 ΠΟΛΥΠΛΕΚΤΗΣ 2 ΕΙΣΟΔΩΝ
Ο Πολυπλέκτης 2 εισόδων (MUX 2x1) έχει δύο εισόδους I0 και I1, μία επιλογή S και μία έξοδο Y, όπως φαίνεται στο Σχήμα 4.1.1.
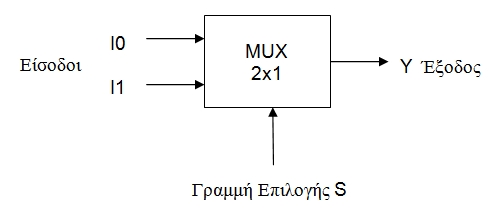
Σχήμα 4.1.1 Πολυπλέκτης 2 εισόδων
Ανάλογα με την τιμή της γραμμής επιλογής S, μία από τις εισόδους I0 και I1 μεταβιβάζεται στην έξοδο Y:
- αν S=0, τότε Y=I0
- αν S=1, τότε Y=I1
όπως φαίνεται στον συνοπτικό Πίνακα Αληθείας του, που παρουσιάζεται στον Πίνακα 4.1.1.
Πίνακας 4.1.1
Συνοπτικός Πίνακας Αληθείας Πολυπλέκτη 2 εισόδων
|
S |
Y |
|
0 |
I0 |
|
1 |
I1 |
Ο Πίνακας Αληθείας του Πολυπλέκτη 2 εισόδων παρουσιάζεται στον Πίνακα 4.1.2.
Πίνακας 4.1.2
Πίνακας Αληθείας Πολυπλέκτη 2 εισόδων
|
S |
I1 |
I0 |
Y |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
Από τον παραπάνω Πίνακα Αληθείας προκύπτει ο χάρτης Karnaugh για την συνάρτηση εξόδου Y συναρτήσει της γραμμής επιλογής S και των εισόδων I0 και I1 που φαίνεται στο Σχήμα 4.1.2.

Σχήμα 4.1.2
Χάρτης Karnaugh για την συνάρτηση εξόδου Y
του Πολυπλέκτη 2 εισόδων
Από τον παραπάνω χάρτη Karnaugh προκύπτει η ακόλουθη συνάρτηση εξόδου Y συναρτήσει της γραμμής επιλογής S και των εισόδων I0 και I1:
Επομένως, το κύκλωμα του Πολυπλέκτη 2 εισόδων μπορεί να υλοποιηθεί χρησιμοποιώντας μία πύλη NOT, δύο πύλες AND δύο εισόδων και μία πύλη OR δύο εισόδων, όπως φαίνεται στο Σχήμα 4.1.3.
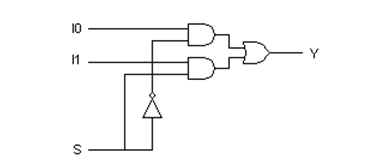
Σχήμα 4.1.3
Υλοποίηση Πολυπλέκτη 2 εισόδων με πύλες
4.1.3 ΠΟΛΥΠΛΕΚΤΗΣ 4 ΕΙΣΟΔΩΝ
Ο Πολυπλέκτης 4 εισόδων (MUX 4x1) έχει τέσσερις εισόδους I0, I1, I2 και I3, δύο γραμμές επιλογής S0 και S1 και μία έξοδο Y, όπως φαίνεται στο Σχήμα 4.1.4.
Σχήμα 4.1.4
Πολυπλέκτης 4 εισόδων
Ανάλογα με τις τιμές των γραμμών επιλογής S1 και S0, μία από τις εισόδους I0, I1, I2 και I3 μεταβιβάζεται στην έξοδο Y:
- αν S1=0 και S0=0, τότε Y=I0
- αν S1=0 και S0=1, τότε Y=I1
- αν S1=1 και S0=0, τότε Y=I2
- αν S1=1 και S0=1, τότε Y=I3
όπως φαίνεται στον συνοπτικό Πίνακα Αληθείας του, που παρουσιάζεται στον Πίνακα 4.1.3.
Πίνακας 4.1.3
Συνοπτικός Πίνακας Αληθείας Πολυπλέκτη 4 εισόδων
|
S1 |
S0 |
Y |
|
0 |
0 |
I0 |
|
0 |
1 |
I1 |
|
1 |
0 |
I2 |
|
1 |
1 |
I3 |
Η συνάρτηση εξόδου Y συναρτήσει των επιλογών S0 και S1 και των εισόδων I0, I1, I2 και I3 είναι η ακόλουθη:
Επομένως, το κύκλωμα του Πολυπλέκτη 4x1 μπορεί να υλοποιηθεί χρησιμοποιώντας δύο πύλες NOT, τέσσερις πύλες AND τριών εισόδων και μία πύλη OR τεσσάρων εισόδων, όπως φαίνεται στο Σχήμα 4.1.5.
Σχήμα 4.1.5
Υλοποίηση Πολυπλέκτη 4 εισόδων με πύλες
4.1.4 ΟΛΟΚΛΗΡΩΜΕΝΑ ΚΥΚΛΩΜΑΤΑ ΠΟΛΥΠΛΕΚΤΩΝ
Στην παράγραφο αυτή θα παρουσιαστεί το ολοκληρωμένο κύκλωμα 74151 της σειράς 74, που περιέχει έναν Πολυπλέκτη 8 εισόδων (MUX 8x1), το οποίο φαίνεται στο Σχήμα 4.1.6.
|
Vcc |
I4 |
I5 |
I6 |
I7 |
A |
B |
C |
|||||||||
|
16 |
15 |
14 |
13 |
12 |
11 |
10 |
9 |
|||||||||
|
74151 |
||||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|||||||||
|
I3 |
I2 |
I1 |
I0 |
Y |
S |
GND |
||||||||||
Σχήμα 4.1.6
Το ολοκληρωμένο κύκλωμα 74151:
ένας Πολυπλέκτης 8 εισόδων
Στο ολοκληρωμένο κύκλωμα 74151, ο Πολυπλέκτης 8 εισόδων (MUX 8x1) έχει οκτώ εισόδους (I0, I1, I2, I3, I4, I5, I6 και I7), τρεις γραμμές επιλογής (C, B και A) και μία έξοδο Y καθώς και την συμπληρωματική έξοδο .
Η λειτουργία του ολοκληρωμένου κυκλώματος 74151 ως Πολυπλέκτη ελέγχεται από την είσοδο ενεργοποίησης S (pin 7):
- όταν S=”0” τότε ανάλογα με τις τιμές των γραμμών επιλογής C, B και A, μία από τις εισόδους I0, I1, I2, I3, I4, I5, I6 και I7 μεταβιβάζεται στην έξοδο Y, δηλαδή το ολοκληρωμένο κύκλωμα 74151 λειτουργεί ως Πολυπλέκτης
- όταν S=”1” τότε ο Πολυπλέκτης είναι απενεργοποιημένος
όπως φαίνεται από τον Πίνακα Αληθείας του ολοκληρωμένου κυκλώματος 74151 που παρουσιάζεται στον Πίνακα 4.1.4.
Πίνακας 4.1.4
Πίνακας Αληθείας του ολοκληρωμένου κυκλώματος 74151
|
S |
C |
B |
A |
Y |
|
1 |
X |
X |
X |
0 |
|
0 |
0 |
0 |
0 |
I0 |
|
0 |
0 |
0 |
1 |
I1 |
|
0 |
0 |
1 |
0 |
I2 |
|
0 |
0 |
1 |
1 |
I3 |
|
0 |
1 |
0 |
0 |
I4 |
|
0 |
1 |
0 |
1 |
I5 |
|
0 |
1 |
1 |
0 |
I6 |
|
0 |
1 |
1 |
1 |
I7 |
4.2 ΕΦΑΡΜΟΓΕΣ ΠΟΛΥΠΛΕΚΤΩΝ
Μία βασική εφαρμογή των Πολυπλεκτών είναι η χρήση τους στην υλοποίηση λογικών συναρτήσεων και συνδυαστικών κυκλωμάτων.
Κάθε λογική συνάρτηση n μεταβλητών μπορεί να υλοποιηθεί με έναν Πολυπλέκτη 2n εισόδων.
Οι μεταβλητές της λογικής συνάρτησης αποτελούν τις γραμμές επιλογής του Πολυπλέκτη.
Oι είσοδοι του Πολυπλέκτη επιλέγονται κατάλληλα από τον Πίνακα Αληθείας της λογικής συνάρτησης: κάθε είσοδος του Πολυπλέκτη είναι "0" ή "1", έτσι ώστε να ικανοποιείται ο Πίνακας Αληθείας της λογικής συνάρτησης.
Η έξοδος του Πολυπλέκτη είναι η λογική συνάρτηση που θέλουμε να υλοποιήσουμε.
Παράδειγμα.
Δίνεται η παρακάτω λογική συνάρτηση Y τριών μεταβλητών A, B και C:
Y(A,B,C)=××+×B×C+ A×B×C
Ο Πίνακας Αληθείας της λογικής συνάρτησης Y παρουσιάζεται στον Πίνακα 4.2.1.
Πίνακας 4.2.1
Πίνακας Αληθείας της λογικής συνάρτησης
Y(A,B,C)=××+×B×C+ A×B×C
|
A |
B |
C |
Y |
|
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
Το πλήθος των μεταβλητών της λογικής συνάρτησης είναι: n=3. Επομένως, η συνάρτηση μπορεί να υλοποιηθεί χρησιμοποιώντας έναν Πολυπλέκτη 8 εισόδων(23x1), όπως φαίνεται στο Σχήμα 4.2.1.
Οι μεταβλητές A, B και C χρησιμοποιούνται ως οι τρεις γραμμές επιλογής του Πολυπλέκτη.
Oι οκτώ είσοδοι I0, I1, I2, I3, I4, I5, I6 και I7 του Πολυπλέκτη επιλέγονται κατάλληλα από τον Πίνακα Αληθείας της λογικής συνάρτησης: κάθε είσοδος του Πολυπλέκτη είναι "0" ή "1", έτσι ώστε να ικανοποιείται ο Πίνακας Αληθείας της λογικής συνάρτησης.
Προφανώς, η έξοδος του Πολυπλέκτη αποτελεί την συνάρτηση Y.
Σχήμα 4.2.1
Υλοποίηση της λογικής συνάρτησης
Y(A,B,C)=××+×B×C+ A×B×C
με Πολυπλέκτη 8 εισόδων
Θέμα για επιπλέον μελέτη.
Κάθε Συνδυαστικό Κύκλωμα n εισόδων και m εξόδων μπορεί να υλοποιηθεί με m Πολυπλέκτες 2n εισόδων.
Παράδειγμα.
Στο παράδειγμα αυτό θα υλοποιηθεί ένα συνδυαστικό κύκλωμα που αναγνωρίζει το πλήθος των “1” ενός 3-bits δυαδικού αριθμού, χρησιμοποιώντας Πολυπλέκτες.
Το συνδυαστικό κύκλωμα έχει τρεις εισόδους A, B και C που χρησιμοποιούνται για τον 3-bits δυαδικό αριθμό. Το πλήθος των “1” του 3-bits δυαδικού αριθμού είναι προφανώς 0 ή 1 ή 2 ή 3. Επομένως, το συνδυαστικό κύκλωμα έχει δύο εξόδους Y1 και Y2 που χρησιμοποιούνται για το πλήθος των “1” του 3-bits δυαδικού αριθμού.
Ο Πίνακας Αληθείας του συνδυαστικού κυκλώματος παρουσιάζεται στον Πίνακα 4.2.2.
Πίνακας 4.2.2
Πίνακας Αληθείας
του συνδυαστικού κυκλώματος
που αναγνωρίζει το πλήθος των “1”
ενός 3-bits δυαδικού αριθμού
|
A |
B |
C |
Y1 |
Y2 |
Πλήθος “1” |
|
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
1 |
1 |
|
0 |
1 |
1 |
1 |
0 |
2 |
|
1 |
0 |
0 |
0 |
1 |
1 |
|
1 |
0 |
1 |
1 |
0 |
2 |
|
1 |
1 |
0 |
1 |
0 |
2 |
|
1 |
1 |
1 |
1 |
1 |
3 |
Το συνδυαστικό κύκλωμα έχει n=3 εισόδους και m=2 εξόδους.
Το πλήθος των μεταβλητών των δύο λογικών συναρτήσεων εξόδων είναι: n=3. Επομένως, κάθε συνάρτηση μπορεί να υλοποιηθεί χρησιμοποιώντας έναν Πολυπλέκτη 8x1(23x1). Άρα, το συνδυαστικό κύκλωμα μπορεί να υλοποιηθεί χρησιμοποιώντας δύο (m=2) Πολυπλέκτες 8x1, όπως φαίνεται στο Σχήμα 4.2.2.
Οι μεταβλητές A, B και C χρησιμοποιούνται ως οι τρεις (κοινές) επιλογές των δύο Πολυπλεκτών.
Oι είσοδοι των δύο Πολυπλεκτών επιλέγονται κατάλληλα από τους Πίνακες Αληθείας των λογικών συναρτήσεων.
Οι έξοδοι των Πολυπλεκτών αποτελούν τις εξόδους του συνδυαστικού κυκλώματος.
Σχήμα 4.2.2
Υλοποίηση του συνδυαστικού κυκλώματος
που αναγνωρίζει το πλήθος των “1”
ενός 3-bits δυαδικού αριθμού
με δύο Πολυπλέκτες 8x1

