Αρχή Λειτουργίας όπως περιγράφεται από τον Ήρωνα

 

 

 

 

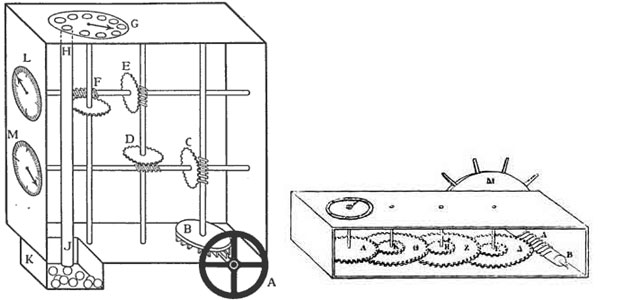
Το όργανο το γνωρίζουμε επακριβώς χάρη στην περιγραφή του Ήρωνα του Αλεξανδρινού, μεγάλου μαθηματικού και μηχανικού της ελληνιστικής περιόδου, την οποία ενσωμάτωσε στο έργο του (όταν είχε διατελέσει διευθυντής του περίφημου Μουσείου της Αλεξάνδρειας, ενός επιστημονικού κέντρου εφάμιλλου με τα σημερινά πολυτεχνεία).

Ακολουθεί μετάφραση της περιγραφής του οδομέτρου από τον Ήρωνα:

 

«…..Ας κατασκευασθεί λοιπόν ένα ξύλινο περίβλημα σαν κιβώτιο, στο εσωτερικό του οποίου θα εγκατασταθεί ολόκληρη η κατασκευή που θα περιγράψουμε. Στη βάση του κιβωτίου τοποθετείται χάλκινος δίσκος[….]ΑΒΓΔ στον οποίον έχουν προσαρμοστεί τα (8) λεγόμενα σκυτάλια (μικρά προεξέχοντα τεμάχια ξύλου. Γι’ αυτά, ας γίνει μια (κατάλληλη) εντομή (άνοιγμα) στον πυθμένα του κιβωτίου δια της οποίας ένας στυλίσκος στερεώς προσκολλημένος εις το κουζινέτο (δηλ. εις τον δακτύλιο περί τον άξονα) ενός από τους τροχούς του οχήματος, μετά από μια περιστροφή του τροχού, εισερχόμενος εις την εντομή του πυθμένος του κιβωτίου θα μετακινήσει ένα σκυτάλιον, ώστε το επόμενο σκυτάλιο να λάβει την ίδια, ακριβώς, θέση και τούτο επαναλαμβάνεται συνεχώς (όσο κινείται το όχημα). Κάθε φορά που ο τροχός πραγματοποιεί 8 στροφές, το τύμπανο με τα σκυτάλια θα επανέρχεται στην αρχική του θέση.

 

 

Στο κέντρο του σκυταλωτού τυμπάνου και καθέτως προς αυτό, καρφώνεται στερεώς (κατά το ένα άκρο του) ένας ατέρμονας κοχλίας, ενώ το άλλο άκρο του, διαπερνά και στερεώνεται εντός οπής στο απέναντι τοίχωμα του κιβωτίου. Δίπλα στον κοχλία τώρα, τοποθετείτε ένα οδοντωτόν τύμπανον του οποίου οι οδόντες εμπλέκονται, ακριβώς, στην έλικα του κοχλία, δηλαδή είναι κάθετον προς τον πυθμένα του κιβωτίου και το οποίον έχει, ομοίως, έναν σταθερώς προσαρμοσμένο άξονα, του οποίου τα άκρα καταλήγουν στα τοιχώματα του κιβωτίου. Ένα τμήμα του άξονος φέρει, επίσης, ελικοειδή εντομή ώστε να γίνεται ένας ατέρμονας κοχλίας. Δίπλα σ’ αυτόν τον κοχλία τοποθετείται, πάλιν, ένα οδοντωτό τύμπανον παραλλήλως προς τον πυθμένα και στο οποίο έχει προσαρμοσθεί, στερεώς, ένας άξονας του οποίου το μεν ένα άκρο, καταλήγει εις τον πυθμένα του κιβωτίου, το δε άλλο εμπήγνυται στα τοιχώματα του κιβωτίου, όπως μια (οριζόντια)ράβδος. Και αυτός, λοιπόν, ο άξονας στο ένα άκρο του φέρει μια έλικα (ατέρμονα κοχλία) η οποία επίσης, προσαρμόζεται πάλι, εις τους οδόντας άλλου τυμπάνου που είναι κάθετο προς τον πυθμένα. Και αυτή η διαδικασία ας επαναλαμβάνεται όσες φορές επιθυμούμε, αρκεί να το επιτρέπει ο διαθέσιμος χώρος του κιβωτίου. Γιατί όσο περισσότερα τύμπανα και κοχλίες τοποθετούνται τόσο μεγαλύτερα είναι τα διαστήματα τα οποία θα μπορούν να μετρηθούν.

 

Έτσι, με κάθε περιστροφή του κοχλία το παρακείμενο τύμπανο θα μετακινηθεί κατά έναν οδόντα οπότε σε διαδρομή μήκους ίσου με 8 περιμέτρους του τροχού, το στερεωμένο σκυταλωτό τύμπανο θα εκτελέσει μια περιστροφή, ενώ το παρακείμενο τύμπανο θα προωθηθεί κατά 1 οδόντα. Εάν π.χ το παρακείμενο τύμπανο έχει 30 οδόντες και περιστραφεί μια φορά από τον κοχλία, θα σημαίνει ότι ο τροχός (του οχήματος) έκανε 30 x 8 = 240 στροφές. Και όταν αυτό το οδοντωτό τύμπανο περιστραφεί πάλι μια φορά, ο μεν προσαρμοσμένος σε αυτό κοχλίας θα κάνει μια περιστροφή, το δε παρακείμενο στον κοχλία τυμπάνιο θα κινηθεί κατά ένα οδόντα. Αν λοιπόν και αυτό το τύμπανο έχει 30 οδόντες, (το οποίον βέβαια μπορούσε να έχει και περισσότερους) και περιστραφεί μια φορά, τότε αυτό θα δηλώνει ότι ο τροχός πραγματοποίησε 7200 (= 30 x 240) στροφές και άρα, αν η περιφέρεια του τροχού είναι 10 πήχεις, το διανυθέν διάστημα θα είναι 72000 πήχεις δηλ. (72000 / 400 =) 180 στάδια. Και αυτά μεν σημειώνονται επί του δευτέρου τυμπάνου. Όταν αυτά τα τύμπανα είναι περισσότερα ενώ έχει αυξηθεί και το πλήθος των οδόντων τους, τότε και το μήκος της διαδρομής θα βρεθεί πολλές φορές μεγαλύτερο, όταν μετρηθεί.

 

Πρέπει λοιπόν η συσκευή να είναι κατά τέτοιο τρόπο κατασκευασμένη ώστε να μην μπορεί να δείξει το όργανο πολύ μεγαλύτερη ένδειξη από την ημερήσια διαδρομή που πραγματοποιεί το όχημα. Διότι είναι δυνατόν καθημερινά να μετρείται η ημερήσια διαδρομή και να τοποθετείται πάλι από την αρχή ο δείκτης για την μέτρηση της επόμενης διαδρομής. Επειδή όμως η περιστροφή του καθενός από τους κοχλίες δεν στρέφει τους παρακειμένους οδόντες με μαθηματική ακρίβεια, εμείς με δοκιμή περιστρέφουμε τον πρώτον κοχλία μέχρις ότου το παρακείμενον προς αυτόν οδοντωτό τύμπανον εκτελέσει μια πλήρη περιστροφή και μετρούμε τον αριθμό των περιστροφών του. Έστω πχ ότι, για να εκτελέσει μια πλήρη περιστροφή το παρακείμενο τύμπανο, απαιτούνται 20 στροφές του κοχλία και ότι τούτο φέρει 30 οδόντες. Δηλ. οι 20 στροφές του σκυταλωτού τυμπάνου προώθησαν 30 οδόντας του παρακείμενου, προς τον κοχλία, τυμπάνου. Αλλά οι 20 στροφές περιστρέφουν (20 x 8 =) 160 σκυτάλια. Τόσες λοιπόν θα είναι και οι στροφές του τροχού. Αυτό ισοδυναμεί με διάστημα 1600 πήχεων (160 στροφές x 10πήχεις/στροφή). Και εάν οι 30 οδόντες αντιστοιχούν σε διαδρομή 1600 πήχεων τότε ο 1 οδόντας, του ανωτέρω οδοντωτού τυμπανίου, θα αντιστοιχεί σε διαδρομή 53 x 1/3 πήχεων. Αν λοιπόν στο ξεκίνημα της ημερήσιας διαδρομής βρεθεί ότι το οδοντωτό τύμπανο έχει μετακινηθεί κατά 15 οδόντας, αυτό σημαίνει μια διαδρομή 800 (53 x 1/3 x 15) πήχεων, δηλ. 2 σταδίων. Θα αναγράψουμε λοιπόν στον μέσον του οδοντωτού αυτού τυμπάνου πήχεις 53 x 1/3.

 

Τα ίδια λοιπόν σκεπτόμενοι θα αναγράψουμε και επί των υπολοίπων οδοντωτών τυμπανίων τους αριθμούς, ώστε από τον αριθμό των μετακινηθέντων οδόντων να γίνεται γνωστή η εκτελεσθείσα διαδρομή. Και για να μην ανοίγουμε το κιβώτιο του οργάνου, κάθε φορά που θέλουμε να μετρήσουμε το μήκος της διαδρομής εξετάζοντας τους οδόντας κάθε τυμπάνου, θα δείξουμε πώς είναι δυνατόν να βρίσκουμε το μήκος της διαδρομής βλέποντας εξωτερικά την ένδειξη του γωνιακού δείκτη σε κάθε κιβωτάριο. Γιατί αυτά τα οδοντωτά τύμπανα τοποθετούνται έτσι ώστε να μην αγγίζουν τις πλευρές του κιβωταρίου, ενώ οι άξονές τους κατά το εξωτερικό μέρος, να διαπερνούν τα τοιχώματα. Οι προεξοχές των αξόνων τώρα, ας έχουν τετράγωνη διατομή, ώστε να μπορούν να δεχθούν μοιρογνωμόνια τετραγωνικής υποδοχή. Έτσι όταν στρέφεται το τύμπανο συμπεριστρέφει και τον άξονα και το μοιρογνωμόνιο. Το άκρο του δείκτου του μοιρογνωμονίου θα διαγράψει κατά την περιστροφή του κύκλο επί της εξωτερικής επιφάνειας του ίδιου τοιχώματος, την οποία διαιρούμε σε τόσα ίσα τόξα, όσος είναι ο αριθμός των οδόντων του τυμπάνου που ευρίσκεται στο εσωτερικό. Ο δείκτης τώρα του μοιρογνωμονίου έχει τέτοιο μέγεθος ώστε να διαγράφει μεγαλύτερο κύκλο και συνεπώς το μήκος του τόξου της περιφέρειας που αντιστοιχεί ανά οδόντα, να είναι μεγαλύτερο. Αυτός ο κύκλος λοιπόν θα έχει την ίδια επιγραφή (δηλ. την ίδια αρίθμηση) με αυτήν που φέρει το εσωτερικό οδοντωτό τύμπανο. Κατ’ αυτόν τον τρόπο με μια παρατήρηση στο εσωτερικό του κιβωταρίου, θα ελέγχουμε το μήκος της διαδρομής.

 

Στην περίπτωση που είναι ακατόρθωτον να μην ακουμπούν όλα τα τυμπάνια επί των τοιχωμάτων του κιβωταρίου, είτε γιατί εμποδίζονται μεταξύ τους είτε από τους παρακείμενους κοχλίες είτε από άλλη αιτία, απομακρύνουμε καθένα απ’ αυτούς τόση απόσταση, ώστε να μην εμποδίζονται από τίποτε. Επειδή όμως τα οδοντωτά τύμπανα, άλλα είναι παράλληλα προς την βάση και άλλα κάθετα, έπεται ότι και οι κύκλοι που γράφονται από τους δείκτες των μοιρογνωμονίων, άλλοι θα είναι επί των καθέτων τοιχωμάτων και άλλοι επί του καλύμματος (δηλ. της άνω έδρας) του κιβωταρίου. Δια τούτο θα πρέπει ένα από τα κάθετα τοιχώματα του κιβωτίου που δεν φέρει μοιρογνωμόνια να γίνει κάλυμμα του κιβωτίου, ώστε αυτό το κάλυμμα να είναι συγχρόνως και τοίχωμα……»

 

 

Πηγή: Το Οδόμετρο από τον Βιτρούβιο κ τον Ήρωνα - yourforum.gr