|
Τα
μαθηματικά του τρόμου
Τάσος Καφαντάρης
Λένε
ότι η Ιστορία δεν θα ξεχώριζε ποτέ από τη μυθοπλασία αν ο Θουκυδίδης δεν
είχε προβεί στην ανάλυση των Πελοποννησιακών Πολέμων, όπως και ότι η
κοινωνιολογία δεν θα είχε γίνει ποτέ επιστήμη αν ο Ιmile Durkheim δεν είχε
μετρήσει τη συχνότητα αυτοκτονιών μεταξύ των καθολικών και των
Διαμαρτυρομένων (Suicide - 1897). Ωστόσο εκείνο που δεν φαντάζονταν ποτέ οι
ερευνητές και της μιας και της άλλης είναι ότι στις απαρχές του 21ου αιώνα η
επιστήμη τους θα γινόταν... ερωμένη των μαθηματικών. Και με ποια αφορμή για
πρόσχημα; Την αντιμετώπιση της διεθνούς τρομοκρατίας!
Στατιστικές του θανάτου
Ο όρος
τρομοκρατία ερμηνεύεται ως «η συστηματική άσκηση τρόμου ως μέσο πίεσης» και
γεννήθηκε στα χρόνια της κυριαρχίας του Ροβεσπιέρου (1793-1974) για να
περιγράψει την άσκηση τρόμου από το κράτος προς τους πολίτες. Στην εποχή
όμως των «δίδυμων πύργων» και του «άξονα του Κακού», οι ρόλοι έχουν - τύποις
- ανατραπεί. Ετσι οι Δυτικοί ξέχασαν το γεφύρωμα του «ψηφιακού χάσματος» με
τους φτωχούς του πλανήτη και βάλθηκαν να διευρύνουν το «θρησκευτικό χάσμα»
με τον Τρίτο Κόσμο ή το «οικονομικό χάσμα» με όσους δεν έχουν να πληρώσουν
τα χρέη τους στις τράπεζες. Οπότε τρομοκρατία σημαίνει πλέον για τους
Δυτικούς τη συστηματική άσκηση τρόμου από τους παρίες της κεφαλαιοκρατίας
προς τα κράτη που τη διακονούν. Ολα αυτά θα παρέμεναν ενασχόληση των
κοινωνιολόγων και των ιστορικών αν το σοκ της πτώσης των δίδυμων πύργων
(11.9.2001) δεν έκα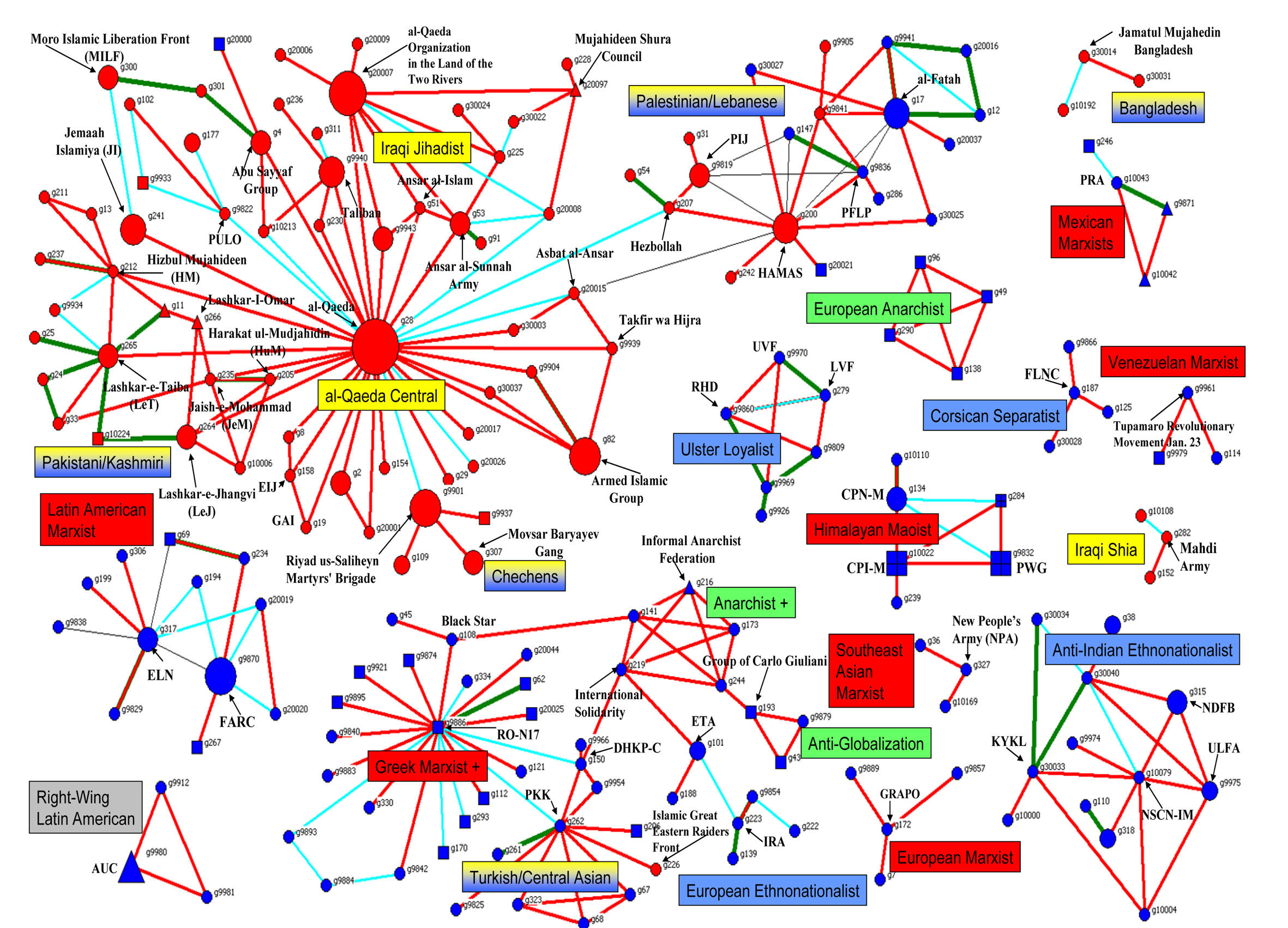 νε
τις διωκτικές αρχές των Δυτικών να ψάχνουν απεγνωσμένα για «τρόπους έγκαιρης
χαρτογράφησης των κινήσεων των τρομοκρατών».
Τότε κάποιος θυμήθηκε την εργασία ενός πρώην τραυματιοφορέα του Α'
Παγκοσμίου Πολέμου, ο οποίος συνέβη να είναι και φυσικομαθηματικός, του
Βρετανού Λιούις Ρίτσαρντσον (Lewis Fry Richardson). Υπό τον τίτλο
«Στατιστικές θανατηφόρων διενέξεων» (Statistics of Deadly Quarrels), ο
Ρίτσαρντσον είχε συλλέξει και ταξινομήσει τα δεδομένα των περισσότερων
πολέμων από το 1820 ως το 1950 και τα είχε αναλύσει σαν νέος Θουκυδίδης. νε
τις διωκτικές αρχές των Δυτικών να ψάχνουν απεγνωσμένα για «τρόπους έγκαιρης
χαρτογράφησης των κινήσεων των τρομοκρατών».
Τότε κάποιος θυμήθηκε την εργασία ενός πρώην τραυματιοφορέα του Α'
Παγκοσμίου Πολέμου, ο οποίος συνέβη να είναι και φυσικομαθηματικός, του
Βρετανού Λιούις Ρίτσαρντσον (Lewis Fry Richardson). Υπό τον τίτλο
«Στατιστικές θανατηφόρων διενέξεων» (Statistics of Deadly Quarrels), ο
Ρίτσαρντσον είχε συλλέξει και ταξινομήσει τα δεδομένα των περισσότερων
πολέμων από το 1820 ως το 1950 και τα είχε αναλύσει σαν νέος Θουκυδίδης.
Ο
χάρτης των τρομοκρατικών οργανώσεων διεθνώς, όπως τον συνέταξαν οι καθηγητές
Victor Asal και Κarl Rethemeyer του Πανεπιστημίου Albany των ΗΠΑ
Θηλαστικά και... τρομοκράτες!
Ο
άνθρωπος που θυμήθηκε τα όσα είχε γράψει ο Ρίτσαρντσον ήταν και αυτός
φυσικομαθηματικός: ο Αμερικανός Ααρον Κλόζετ (Aaron Clauset). Στην αρχή των
σπουδών του είχε προσπαθήσει να πάρει και πτυχίο κοινωνιολογίας, αλλά την
εγκατέλειψε όταν διαπίστωσε πως «ακόμη και η μηχανική του Νεύτωνα είναι πιο
προχωρημένη και από την καλύτερη κοινωνική θεωρία που έχουμε τώρα» - όπως
δήλωσε σε συνέντευξή του. Αντ' αυτής γοητεύθηκε από τις δυνατότητες
μαθηματικής προσομοίωσης που του έδιναν οι υπολογιστές. Για παράδειγμα,
δόμησε ένα μαθηματικό μοντέλο που του έδινε την κατανομή παγκοσμίως των
4.000 ειδών θηλαστικών. Οταν συζήτησε την πιθανότητα μοντελοποίησης της
διεθνούς τρομοκρατίας με τον πληροφορικάριο φίλο του Maxwell Young - το 2003
-, συνειδητοποίησε ότι θα μπορούσαν να εφαρμόσουν τις ίδιες μαθηματικές
τεχνικές που είχε χρησιμοποιήσει για τα θηλαστικά και... στους τρομοκράτες.
Το μόνο που του έλειπε ήταν μια βάση δεδομένων αντίστοιχη εκείνης του
Ρίτσαρντσον, για τις τρομοκρατικές επιθέσεις αυτή τη φορά.
Ο
«νόμος της ισχύος»
Με την αρωγή ενός τρίτου που εντάχθηκε στην παρέα, του πολιτικού επιστήμονα
στο βρετανικό Πανεπιστήμιο του Εσεξ Kristian Gleditsch, εντόπισαν αργότερα
το ζητούμενο στο ίδρυμα της Οκλαχόμα, Memorial Institute for the Prevention
of Terrorism: Είχαν καταγράψει 36.018 τρομοκρατικές ενέργειες σε 187 χώρες
μεταξύ των ετών 1968-2008. Η ομάδα επέλεξε 13.000 από αυτές, οι οποίες είχαν
θανατηφόρα αποτελέσματα, και εξέφρασε σε γράφημα την αντιπαράθεση της
συχνότητάς τους με τη σφοδρότητά τους. Αυτό που προέκυψε ήταν αναπάντεχο: Οι
πιο συχνές επιθέσεις που εκπορεύονταν από την ίδια οργάνωση είχαν λιγότερα
θύματα, ενώ οι πιο αραιές κατέληξαν σε εκατόμβες. Η καμπύλη του γραφήματος
αυτού ήταν περίπου σαν «L», που στα μαθηματικά λέγεται «ανεξαρτησία
κλίμακας» (scale invariance). Ωστόσο η καμπύλη αυτής της μορφής είναι
ακριβώς εκείνη που εκφράζει τον λεγόμενο «νόμο της ισχύος». Με δυο λόγια, η
ως τότε αντίληψη ότι υπήρχε «μικρή» και «μεγάλη» τρομοκρατία, χωρίς σχέση
μεταξύ τους, δεν έστεκε.
Πρέπει
να τις... σκοτώνεις «μικρές» Οπως εξήγησε ο Κλόζετ στις
αντιτρομοκρατικές υπηρεσίες, η εφαρμογή του νόμου της ισχύος στα
τρομοκρατικά δρώμενα ενέχει την εφαρμογή στις οργανώσεις αυτές της
δαρβινικής εξέλιξης: «Από την ανάλυση των δεδομένων προκύπτει ότι όσο
μεγαλύτερη είναι μια τρομοκρατική οργάνωση τόσο συχνότερα επιτίθεται. Οι
περισσότερες ομάδες αρχίζουν τη δράση τους όταν είναι μικρές, κερδίζουν φήμη
και προσηλύτους με κάθε τους χτύπημα και μεγαλώνουν. Αφ' ης στιγμής φθάσουν
σε κάποιο μέγεθος, η διάρκειά τους είναι εγγυημένη. Το να εξοντώσεις πια
κάποιο σημαίνον στέλεχός τους - χτυπώντας τον με τα πυρά τηλεκατευθυνόμενου
αεροπλάνου, για παράδειγμα - δεν θα έχει εφεξής τη διαλυτική επίδραση που θα
είχε όσο ήταν μικρές σε μέγεθος» είπε. Και το έκανε πιο σαφές: «Οπως ακριβώς
συμβαίνει με τις μικρές επιχειρήσεις που μόλις βγαίνουν στην αγορά, οι
τρομοκρατικές ομάδες απαρτίζονται από εξαιρετικά φιλόδοξα άτομα που θέλουν
να βγάλουν ένα προϊόν (μια τρομοκρατική επίθεση). Και οι μεν και οι δε έχουν
το άγχος να αναπτυχθούν, ειδεμή θα σβήσουν. Και όσο η επιχείρηση ή η ομάδα
είναι μικρή σε μέγεθος, το να της φύγει ένα κορυφαίο στέλεχος μπορεί να
επιφέρει τη διάλυση. Οταν όμως έχουν γίνει μεγάλες, με πολλά στελέχη, μια
τέτοια απώλεια δεν είναι πια κρίσιμη».
Μίσος
με τη βοήθεια του... Θεού Ενα άλλο σημαντικό στοιχείο που προέκυψε από την
έρευνά του είναι η διαφοροποίηση της τωρινής τρομοκρατίας από τις
προγενέστερες. Συγκεκριμένα το τωρινό «τέταρτο κύμα τρομοκρατών», που
διακατέχεται από θρησκευτικό φανατισμό, παρουσιάζει την εξής ειδοποιό
διαφορά από τους αναρχικούς του 19ου αιώνα, τους αντιαποικιοκράτες
εξεγερμένους των αρχών του 20ού ή τους επαναστάτες της εποχής του Ψυχρού
Πολέμου: «Οι θρησκευτικές ομάδες επιταχύνουν τα χτυπήματά τους πολύ ταχύτερα
από τις πολιτικές ομάδες. Ο λόγος είναι ότι μεγεθύνονται πολύ ταχύτερα,
μάλλον επειδή η δεξαμενή υποψήφιων μελών είναι πολύ μεγαλύτερη και τους
είναι πολύ πιο εύκολος ο προσηλυτισμός τους» λέει.
Η
επομένη 11η Σεπτεμβρίου... Από τότε που πρωτοασχολήθηκαν με το θέμα ο Κλόζετ
και οι συνεργάτες του έχουν προβεί σε δύο επιστημονικές δημοσιεύσεις, αλλά
είναι πλέον πολύ προσεκτικοί ως προς τη δυνατότητα του μοντέλου τους να
προβλέπει τρομοκρατικά χτυπήματα. Η επιφυλακτικότητά τους δεν έχει να κάνει
τόσο με τη στιβαρότητα των μαθηματικών τους όσο με τον αντίκτυπο τέτοιων
ανακοινώσεων. Το 2005, όταν η πρώτη εργασία τους όδευε ακόμη προς
δημοσίευση, οι εφημερίδες την έκαναν πρωτοσέλιδο, με τίτλους όπως: «Φυσικοί
προβλέπουν η επόμενη 11η Σεπτεμβρίου να συμβεί σε επτά χρόνια». Επεξηγώντας
την τότε πρόβλεψη, ο Κλόζετ είπε: «Αυτό που είχαμε πει ήταν πως αν το μέλλον
έχει ακριβώς τις παραμέτρους του παρελθόντος και εφόσον οι παραδοχές του
μοντέλου μας είναι σωστές τότε αυτό είναι το αναμενόμενο. Αλλά δεν έχω
εμπιστοσύνη στο ότι αυτή θα είναι η ακριβής χρονολογία». Σημειώνουμε εδώ ότι
αυτές τις «διορθωτικές δηλώσεις» ο Κλόζετ τις έκανε αφού προσελήφθη στο
στενά συνεργαζόμενο με το Πεντάγωνο Ινστιτούτο Ερευνών της Σάντα Φε (στο
Πανεπιστήμιο του Νέου Μεξικού). Και βεβαίως τα επτά χρόνια της πρόβλεψης
συμπληρώνονται του χρόνου.
Χάος,
fractals και «μετάβαση φάσης» Το εγχείρημα του Κλόζετ και της παρέας
του μπορεί να ξεκίνησε ως ερασιτεχνικό και να κατέληξε άκρως επαγγελματικό
(σήμερα είναι σύμβουλος τουλάχιστον έξι αντιτρομοκρατικών φορέων στις ΗΠΑ)
αλλά επ' ουδενί λόγω δεν σημαίνει ότι είναι ο μόνος που στήνει μαθηματικά
μοντέλα πρόγνωσης τρομοκρατικών φαινομένων. Για παράδειγμα, σε συναφές με το
θέμα συνέδριο που έγινε τον Αύγουστο 2009 στο Ινστιτούτο της Σάντα Φε
παρόμοια μαθηματικά μοντέλα παρουσίασαν οι Peter Dodds και Chris Danforth
από το Πανεπιστήμιο του Βερμόντ. Αλλά και εκτός αυτών, εντυπωσιακά
προγράμματα πρόγνωσης τρομοκρατικής δράσης έχουν να επιδείξουν ερευνητές
όπως ο καθηγητής Μαθηματικών του ΜΙΤ Jonathan Farley, ο Neil Johnson στο
Πανεπιστήμιο του Μαϊάμι (πρώην καθηγητής στην Οξφόρδη), ο Ρώσος Vladimir
Lefebvre στο Πανεπιστήμιο της Καλιφόρνιας Irvine ή ο πακιστανός Nasrullah
Memon στο Πανεπιστήμιο της Νότιας Δανίας (ως πέρυσι στο Hellenic American
University της Αθήνας). Ωστόσο τι είναι αυτό που συνδέει όλους αυτούς και
από πού αντλούν τα εργαλεία τους;
Ο
κοινός τόπος εντοπίζεται στην κληρονομιά που άφησε πίσω του ο αυστριακός
φυσικός του 19ου αιώνα Ludwig Boltzmann. Ηταν αυτός που έθεσε τα θεμέλια της
«στατιστικής μηχανικής», για να μελετήσει μαθηματικά τη συμπεριφορά μεγάλων
συνόλων σωματιδίων. Κατ' ουσίαν ήταν μια παραλλαγή της θεωρίας των
πιθανοτήτων. Ωστόσο γύρω στο 1970 νέα θεωρητικά εργαλεία ήρθαν να ενισχύσουν
αυτή την κληρονομιά: η θεωρία του χάους, η θεωρία των φράκταλ και η θεωρία
της μετάβασης φάσης. Η πρώτη εξετάζει το πώς προκύπτει πολύπλοκη και
απρόβλεπτη συμπεριφορά από μικρές αλλαγές στις αρχικές συνθήκες, η δεύτερη
μας δίνει τις συνθήκες διαμόρφωσης ατέρμονων επαναλήψεων της ίδιας δομής σε
διάφορες κλίμακες και η τρίτη μελετά πότε ένα σύστημα φθάνει σε «ακραία
κατάσταση» και αλλάζει φάση (π.χ. από στερεό γίνεται ρευστό).
Τα
«σωματίδια» των κοινωνικών δικτύων Η εφαρμογή των μαθηματικών πλαισίων που
αναπτύχθηκαν βάσει αυτών των θεωριών σε πολύπλοκα συστήματα - από τα
σωματίδια της ύλης ως τα βιολογικά και τα κοινωνικά συστήματα - αποδίδει
τώρα τους θεαματικούς καρπούς που βλέπουμε. Και αν για την ανόργανη ύλη ή
για τα ζώα και τα φυτά είχαμε αρκετές βάσεις δεδομένων, το έλλειμμα των
κοινωνιολόγων σε παγκόσμια δεδομένα για την ανθρώπινη συμπεριφορά ήρθε να το
καλύψει το Διαδίκτυο. Τώρα, μέσω της ανάλυσης των διασυνδέσεων που χτίζουμε
στα λεγόμενα κοινωνικά δίκτυα (Social Networks), οι ερευνητές - είτε των
πανεπιστημίων είτε της αντιτρομοκρατικής υπηρεσίας - μπορούν στο άψε-σβήσε
να βγάλουν την πρόγνωση αν η «παρεούλα μας» θα παραμείνει κύμβαλο αλαλάζον ή
θα μετεξελιχθεί σε τρομοκρατικό πυρήνα.
Είναι
όμως επιστημονικά πλήρες ένα μαθηματικό μοντέλο που ανιχνεύει συσχετισμούς
και «αλλαγές φάσης» χωρίς να εξετάζει αφετηρίες, αίτια και κίνητρα στη λήψη
των ανθρώπινων αποφάσεων; Ως προς το ερώτημα αυτό, ενδιαφέρουσα ήταν η
σχετική απάντηση που έδωσε σε συνέντευξή του ο προαναφερθείς Ααρον Κλόζετ: «Οταν
το καλοσκέφτεσαι, σου φαίνεται παράξενο. Σε αυτές τις οργανώσεις υπάρχουν
σκεπτόμενα άτομα, με οικογένειες, στόχους, ιδανικά και όλα τα συναφή. Κι
όμως εγώ τα αντιμετωπίζω λίγο-πολύ σαν να είναι στοιχειώδη σωματίδια της
ύλης. Ωστόσο τα... ίχνη που αφήνει η δράση τους μιλάνε από μόνα τους».
Η
Αραβική άνοιξη είχε προβλεφθεί Δεν είναι όμως μόνον αυτών τα ίχνη που
μιλάνε. Ενας συνοδοιπόρος του Κλόζετ στη μαθηματική ανάλυση των ανθρώπινων
δραστηριοτήτων είναι και ο Yaneer Bar-Yam, πρόεδρος του New England Complex
Systems Institute της Βοστώνης. Ο ερευνητής αυτός και η ομάδα του είχαν
αναπτύξει ένα επίσης προγνωσιακό μοντέλο, βασισμένο στη θεωρία της μετάβασης
φάσης, το οποίο του έδωσε εγκαίρως στοιχεία για εξέγερση στις αραβικές
χώρες. Με τα πορίσματά τους υπό μάλης, κατέθεσαν στις 13 Δεκεμβρίου 2010
αναφορά προς τη Γερουσία των ΗΠΑ, όπου την προειδοποιούσαν ότι η Βόρεια
Αφρική ήταν κοινωνικά έτοιμη να εκραγεί. Λίγες ημέρες μετά εκδηλώθηκε η
λαϊκή εξέγερση στην Τυνησία, για να ακολουθήσουν εκείνες της Αιγύπτου και
της Λιβύης. Η ποιοτική διαφορά όμως της πρόγνωσής τους από τα αμιγώς
«αντιτρομοκρατικά μοντέλα» ήταν ότι εντόπιζαν τα αίτια: δήλωναν ξεκάθαρα
στην αναφορά τους ότι αν η αύξηση των τιμών τροφίμων παγκοσμίως συνεχιστεί,
τότε μεταξύ του Ιουλίου 2012 και του Αυγούστου 2013 η κοινωνική εξέγερση θα
γίνει παγκόσμια!
«Χρηματιστηριακή τρομοκρατία», η νέα απειλή Και, προκειμένου να εμπεδώσουμε καλύτερα το μήνυμα
πολιτικοί και απλοί πολίτες, οι ερευνητές αυτοί «ξαναχτύπησαν» στις 21
Σεπτεμβρίου 2011, με νέο ανακοινωθέν (βλ. http: //necsi. edu/research/social/food_prices.
pdf), όπου αποκαλύπτουν τη δράση της «χρηματιστηριακής τρομοκρατίας»: Ούτε
λίγο ούτε πολύ, εντοπίζουν τη ρίζα των δεινών που ζούμε και θα ζήσουμε στον
νόμο χρηματιστηριακής απορρύθμισης (γνωστόν αγγλιστί ως Commodity Futures
Modernization Act of 2000 - CFMA) που εισήγαγε στις 21 Δεκεμβρίου 2000 ο
τότε πρόεδρος των ΗΠΑ Μπιλ Κλίντον. Στο συμπέρασμα της εργασίας τους οι
συγγραφείς τονίζουν: «Αυτή η ανάλυση συνδέει το σκάσιμο της φούσκας στην
αγορά ακινήτων των ΗΠΑ και την οικονομική κρίση του 2007-2008 με την αύξηση
των τιμών τροφίμων παγκοσμίως». Τα κεφάλαια που εγκατέλειψαν την αγορά
ακινήτων πήγαν να φουσκώσουν τις τιμές τροφίμων. Ετσι φτάσαμε τον Σεπτέμβριο
του 2010 να έχουμε 140 εκατομμύρια τόνους δημητριακών καταχωνιασμένους σε
αποθήκες παγκοσμίως - ποσότητα που θα αρκούσε να θρέψει 440 εκατομμύρια
ανθρώπους - να παίζουν κρυφτούλι στο πλαίσιο χρηματιστηριακών παιχνιδιών,
ενώ ο Τρίτος Κόσμος λιμοκτονούσε.
Τώρα...
πόση έννοια έχει πια η μαθηματική ανάλυση των κινήσεων όσων θέλουν «να
καταλάβουν τη Wall Street»; Θα πει άραγε το πρόγραμμα στον χειριστή του αν
το επόμενο τρομοκρατικό χτύπημα «ψήνεται» από το πλήθος ή από τον εργοδότη
του;
Η
«ΧΡΗΜΑΤΙΣΤΗΡΙΑΚΗ ΤΡΟΜΟΚΡΑΤΙΑ» ΣΤΑ ΤΡΟΦΙΜΑ 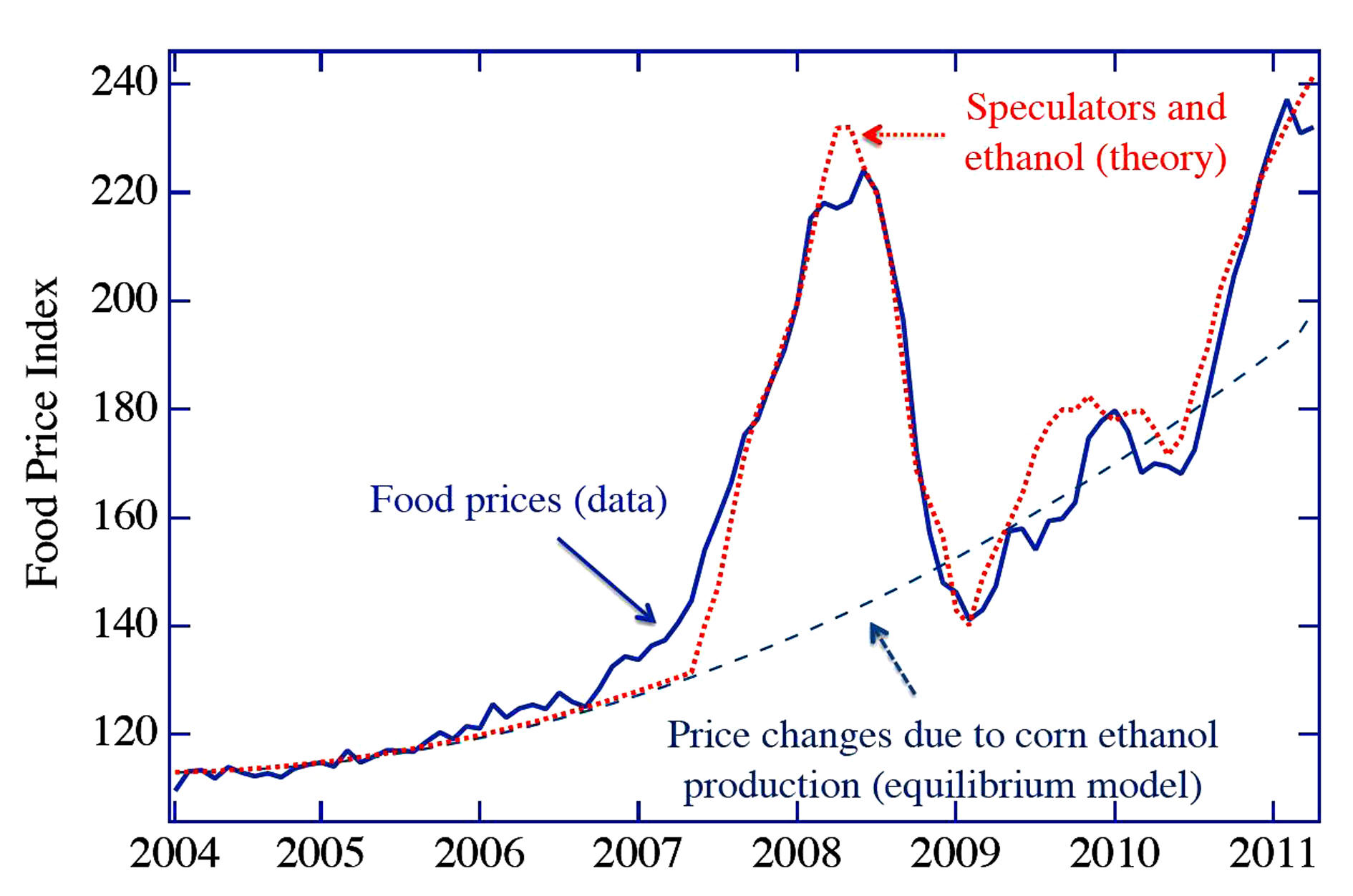
Το «κατηγορώ» του μοντέλου Bar-Yam: με
διακεκομμένη γραμμή η φυσιολογική αύξηση των τιμών τροφίμων λόγω μετατροπής
του καλαμποκιού σε αιθανόλη, με κόκκινη το σπεκουλάρισμα των χρηματιστών και
με μπλε οι τιμές που μας προέκυψαν
*Απόδοση των όρων του διαγράμματος:
Food Price Index = Δείκτης τιμών τροφίμων
Food prices (data) = Τελικές τιμές τροφίμων
Price changes due… = Αύξηση τιμών λόγω μετατροπής σε αιθανόλη
Speculators = Επίδραση χρηματιστηρίου και αιθανόλης)
Έγκλημα και... μαθηματικά!
Ε, λοιπόν, οι μαθηματικοί έχουν βαλθεί να μας αποδείξουν τη χρησιμότητά
τους. Το ξεκίνησαν τον Μεσαίωνα, έπειτα από τους αιώνες λήθης που τους
χώρισαν από την αίγλη των Ευκλείδη, Αρχιμήδη και Πυθαγόρα, όταν τους
πρωτοζητήθηκε να «σπάσουν τον κώδικα» κάποιου κρυπτογραφημένου μηνύματος του
εχθρού.
ΚΟΡΥΦΗ |