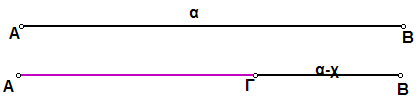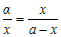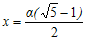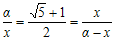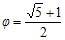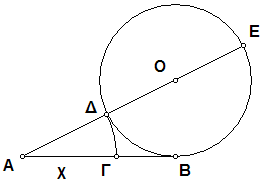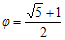Χρυσός αριθμός φ

 

Το πρόβλημα της χρυσής τομής είναι:

Να χωριστεί ένα δοσμένο ευθύγραμμο τμήμα α σε δύο μέρη έτσι ώστε το μεγαλύτερο να είναι μέσον ανάλογο του όλου και του υπολοίπου

  

Δηλαδή 

  

 

ή   x2 = α.(α-x)  ή  x2 +αx-α2 =0 . Η θετική λύση της εξίσωσης αυτής είναι: 

  

 

 

από όπου προκύπτει ότι:

  

 

που είναι η αναλογία της «χρυσής τομής»

 

 

Ο παραπάνω λόγος συμβολίζεται διεθνώς με το γράμμα φ, δηλαδή

 

 

 

 Ο συμβολισμός προέρχεται από το όνομα του γλύπτη της κλασικής αρχαιότητας Φειδία ο οποίος κατασκεύασε τον Παρθενώνα. ο αρχαίοι Έλληνες φιλόσοφοι διαπίστωσαν ότι όπου εμφανίζεται ο λόγος φ (αρχιτεκτονική, γλυπτική κλπ) δημιουργεί τη αίσθηση της αρμονίας

 

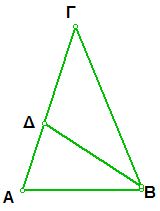
Γεωμετρική κατασκευή

 

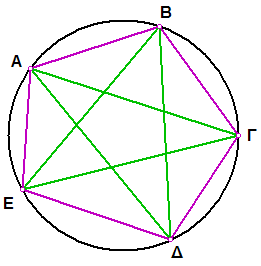
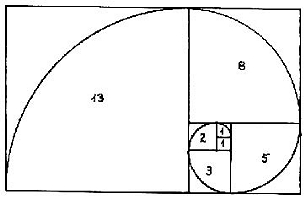
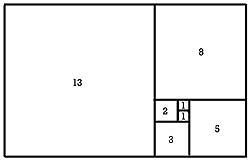
Έστω ΑΒ = α και ΑΓ = x το μεγαλύτερο από τα τμήματα που χωρίζεται το ΑΒ από το Γ. Τότε το ΒΓ=α-x και ισχύει ΑΓ2 = ΑΒ.ΓΒ  ή  x2 = α(α-x)  ή  x(α+x)=α2 Έτσι γράφομε κύκλο (Ο,α/2) που εφάπτεται στο ΑΒ στο σημείο Β και φέρουμε την ΑΟ που τέμνει τον κύκλο στα Δ και Ε. Τότε ΑΒ2= ΑΔ.ΑΕ = ΑΔ(ΑΔ+ΔΕ) =ΑΔ(ΑΔ+ΑΒ)

Δηλαδή α2 = ΑΔ(ΑΔ+α) και το ΑΔ είναι το ζητούμενο τμήμα

 

 

Άλλες εκφράσεις του ίδιου προβλήματος

 1. Υπάρχει αριθμός τέτοιος ώστε εάν τον υψώσεις στο τετράγωνο να αυξηθεί κατά μία μονάδα;

2. Υπάρχει αριθμός τέτοιος ώστε εάν τον ελαττώσεις κατά μία μονάδα να αντιστραφεί;

3. Το κανονικό δεκάγωνο εγγεγραμμένο σε  κύκλο.  Η ακτίνα του κύκλου είναι βέβαια μεγαλύτερη από την πλευρά του. 

4 Η ακολουθία Fibonacci 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025 . . Καθένας από τους όρους της προκύπτει από το άθροισμα των δύο που προηγούνται.  αν = αν-1 + αν-2 .

Αν φτιάξουμε μια ακολουθία με όρους τους λόγους των διαδοχικών όρων της ακολουθίας θα έχουμε   1, 2, 3/2,  5/3, 8/5, 13/8, 21/13, 34/21, 55/24, 89/55,  144/89,…

  Θα διαπιστώσουμε ότι «συγκλίνει» σε κάποιο αριθμό.

Η απάντηση σε όλα είναι ο αριθμός

  

 

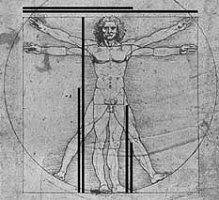
  Ο Leonardo da Vinci μας έμαθε ότι εάν το ύψος οποιουδήποτε ανθρώπου διαιρεθεί με το ύψος στο οποίο βρίσκεται ο αφαλός του το αποτέλεσμα θα είναι ίσο με φ.

1700 χρόνια νωρίτερα είχε ασχοληθεί μαζί του ο Ευκλείδης αλλά τα  βιβλία που αναφέρονται σε αυτόν δεν είναι κυρίως βιβλία μαθηματικών. Είναι βιβλία διαπνεόμενα από  μυστικισμό και μας μιλούν για το σουξέ που είχε ο φ διατηρούμενος σαν λείψανο από τους αρχαίος μύστες, μας λένε πως ο φ είναι ένα μυστικό της ομορφιάς το οποίο διατηρήθηκε και πως δεν είναι τυχαίο ότι η πρόσοψη του Παρθενώνα εγγράφεται σε ένα χρυσό ορθογώνιο με πλευρές που έχουν λόγο φ.

Στην ευρωπαϊκή παράδοση ο όρος «χρυσή τομή» κάνει την εμφάνισή του στο έργο του Leorardo da Vinci σε γλώσσα λατινική ως sectio aurea.

 

Χρυσό τρίγωνο

Χρυσό λέγεται κάθε ισοσκελές  τρίγωνο στο οποίο ο  λόγος της μεγάλης πλευράς προς τη μικρή θα είναι ίσος με φ. Κάθε ισοσκελές με γωνία κορυφής 360 είναι χρυσό.

Μπορούμε να το αποδείξουμε φέρνοντας τη διχοτόμο μιας από τις παρά τη βάση γωνίες – στο σχήμα της Β – τα τρίγωνα ABΓ και ABΔ είναι όμοια,  οπότε (AΓ) = φ(AB)

Η διχοτόμος της γωνίας Β = 720 δημιουργεί στην απέναντι πλευρά χρυσή τομή

 

 

 

 

Το αστέρι των Πυθαγορείων

Το σύμβολο της αδελφότητας των Πυθαγορείων ήταν το «πεντάγραμμο», το αστέρι δηλαδή που σχηματίζεται από τις πέντε διαγωνίους του κανονικού πενταγώνου. Αποδεικνύεται ότι κάθε πλευρά του «πενταγράμμου» διαιρεί τις δύο άλλες σε χρυσή τομή. Κάθε γωνία του «πενταγράμμου» είναι 360. Στο τρίγωνο ΑΓΔ του σχήματος η ΓΕ διχοτομεί τη γωνία ΑΓΔ άρα τέμνει κατά χρυσή τομή την ΔΓ.

 

  

Ο Πυθαγόρας πρώτος παρατήρησε ότι τα φυτά και τα ζώα δεν μεγαλώνουν τυχαία, αλλά σύμφωνα με ακριβείς μαθηματικούς κανόνες. Δεν είναι τυχαία δηλαδή τα όμορφα σχέδια των λουλουδιών. Οι αρχαίοι Έλληνες βρήκαν ότι τα σχέδια των λουλουδιών βασίζονται σε γεωμετρική αναλογία. Επίσης η ακολουθία κάνει την εμφάνισή της στη διάταξη των φύλων γύρω από το μίσχο. Εμφανίζεται ακόμα και στην ανάπτυξη των βελόνων αρκετών ειδών ελάτου, καθώς επίσης και στη διάταξη των πετάλων στις μαργαρίτες και τα ηλιοτρόπια. Μερικά κωνοφόρα δένδρα παρουσιάζουν τη σειρά αριθμών στη δομή της επιφάνειας των κορμών τους, ενώ τα φοινικόδεντρα στους δακτυλίου

 

Χρυσό σπιράλ, κοχύλια και ηλιοτρόπια

Εάν αντί να χρησιμοποιήσουμε το ψαλίδι σχεδιάσουμε πάνω  στο αρχικό ορθογώνιο τις τομές και σε κάθε τετράγωνο που δημιουργείται σχεδιάσουμε τα αντίστοιχα τεταρτοκύκλια θα έχουμε αρχίσει να φτιάχνουμε το χρυσό ελικοειδές, το σπιράλ που σχεδιάζει η φύση και το διακρίνουμε

 

 

 

 

Αργότερα ο Leonardo Da Vinci ζωγράφισε το πρόσωπο της Mona Lisa ώστε αυτό να χωράει τέλεια σε ένα χρυσό ορθογώνιο και δόμησε τον υπόλοιπο πίνακα γύρω από το πρόσωπο χωρίζοντάς τον επίσης σε χρυσά ορθογώνια. Ο Mozart διαίρεσε μεγάλο αριθμό από τις σονάτες του σε δύο μέρη, η χρονική αναλογία των οποίων αντιστοιχεί στη χρυσή τομή, τον αριθμό φ, αν και υπάρχει σημαντική διχογνωμία για το κατά πόσο αυτό έγινε σκόπιμα.

Το Φ στη Βίβλο του Ισλάμ

Η λέξη Κοράνι, πιο σωστά στα Αραβικά Κουράν - Qur'an, προέρχεται από το ρήμα κάρα'α - qara'a που σημαίνει, απαγγέλλω κι αποτελείται από 114 κεφάλαια (Σούρα). Ο αριθμός 114 είναι διαιρετέος με το 19, ήτοι 19*6=114. Το 114 προκύπτει από τη διαίρεση του κύκλου με το π, ήτοι 360/π, όπου π=3,14159 και το 19 εκτός του ότι είναι ο Μετωνικός Αριθμός, προκύπτει επίσης σαν δεκαπλάσιο του π/Φ, όπου Φ=1,618034

Το ανθρώπινο σώμα έχει δομηθεί και αναπτύσσεται σε αναλογίες Φ. Δεν είναι τυχαίο ότι πολλές «ανατολίτικες θρησκείες» και κινήματα στα πλαίσια της διδασκαλίας τους για διαλογισμό και την «αυτοσυγκέντρωση και στο λεγόμενο «γιόγκα» η στάση του ανθρώπινου σώματος γίνεται κατά αυτό τον τρόπο έτσι ώστε τα «κεντρικά - κομβικά» σημεία του σώματος να βρίσκονται σε αναλογίες Φ. Αν θέλει κανείς να δει ένα χρυσό ορθογώνιο αρκεί να κοιτάξει μια πιστωτική κάρτα το σχήμα της οποίας είναι ακριβώς αυτό. Τέλος υπάρχουν καταγραφές που μιλούν για την ύπαρξη του Φ στην δομή του DNA.