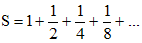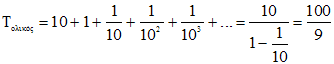Η έννοια του απείρου είναι γνωστή από την αρχαία εποχή προκάλεσε μάλιστα  από την αρχή διαφορές, αντινομίες, πολλές από τις οποίες αποτελούν μέχρι σήμερα αντικείμενο μελέτης. Μην ξεχνάμε ότι η έννοια του ορίου έγινε γνωστή πολύ αργότερα. Θα αρκεστούμε στα 2 γνωστά σοφίσματα του Ζήνωνα του Ελεάτη (496-429 π.Χ.). Αυτά σήμερα έχουν ιστορική μόνο σημασία.

1. Το Παράδοξο της Διχοτομίας ή το βέλος και ο στόχος

Με το  παράδοξο αυτό ούτε λίγο ούτε πολύ καταλήγουμε στο συμπέρασμα ότι «η κίνηση είναι αδύνατη»  διότι ότι  κινείται, πριν φτάσει στο τέρμα του πρέπει να φτάσει στη μέση της πορείας του.

Ο Ζήνωνας λέει ότι για να μεταβεί ένα σώμα από μια θέση Α σε μια θέση Β οφείλει να διανύσει το μισό της απόστασης ΑΒ. Στη συνέχεια το μισό του υπολοίπου, ακολούθως το μισό του νέου υπολοίπου και ούτω καθ’ εξής. Οι αποστάσεις αυτές γίνονται συνεχώς μικρότερες, αλλά απαιτείται για κάθε μια απ’ αυτές ένας ορισμένος χρόνος για να διανυθεί. Και έτσι συμπέρανε ότι «το άθροισμα ενός απείρου αριθμού ορισμένων χρονικών διαστημάτων οφείλει να είναι άπειρο». Κατά συνέπεια η πραγματικότητα της κίνησης και ακριβέστερα της έκτασης είναι αδύνατη.

Ας υποθέσουμε για παράδειγμα έλεγε ο Ζήνωνας ότι έχουμε μια απόσταση (ΑΒ) = 2 Κm και η ταχύτητα του κινητού είναι υ = 1 Km/min. Τότε το μισό της απόστασης έστω (ΑΜ₁) θα διανυθεί σε χρόνο t₁ = 1 min ,το μισό της υπόλοιπης απόστασης το (Μ₁Μ₂) σε χρόνο   t₂ = 1/2 ,το μισό του υπολοίπου, δηλαδή το (Μ₂Μ₃) σε χρόνο t₃ = 1/4 min. Ο Ζήνωνας ισχυρίζεται ότι αυτή η διαδικασία θα συνεχίζεται μέχρι το άπειρο και έτσι θα υπάρχει πάντα ένα κομμάτι που θα απομένει. Δηλαδή το κινητό δεν θα φτάσει ποτέ στο σημείο Β. Βλέπουμε εδώ πόσο θα διευκόλυνε τα πράγματα η έννοια του ορίου. Γιατί είναι γνωστό ότι  ο συνολικός χρόνος που απαιτείται για να διανυθεί η απόσταση (ΑΒ) είναι 2 λεπτά και δίνεται από τη σχέση 

2. Το Παράδοξο του Αχιλλέα και της Χελώνας.

Ο Αχιλλέας εκτός των άλλων αρετών που είχε όπως αναφέρει ο Όμηρος φημιζόντανε και για την ταχύτητά του – γρηγοροπόδαρος - αναφέρεται στον Όμηρο. Και όμως ο Ζήνωνας ισχυρίζεται ότι δεν μπορεί να φτάσει ποτέ μια χελώνα που έστω προπορεύεται  μια απόσταση.

Ας υποθέσουμε ότι η χελώνα προπορεύεται του  Αχιλλέα 100 m και ότι η ταχύτητα υ_A του Αχιλλέα είναι υ_A=10 m/sec και της χελώνας, υ_x, είναι υ_x=1 m/sec. Τότε ο Αχιλλέας σε χρόνο t₁=10 sec θα διανύσει την απόσταση (ΑΧ₁)=100 m, την οποία τον προσπερνούσε η χελώνα. Κατά τη διάρκεια αυτού του χρόνου t₁ η χελώνα θα διανύσει το διάστημα       Χ₁Χ₂ =10 m. Στη συνέχεια για να διατρέξει αυτή την απόσταση ο Αχιλλέας θα χρειαστεί χρόνο t₂ =1 sec. Κατά το χρόνο t₂ η χελώνα θα διανύσει το διάστημα Χ₂Χ₃ =1 m και ο Αχιλλέας θα το διατρέξει σε χρόνο t₃ =1/10 sec. Η κίνηση αυτή θα συνεχίζεται επ’ άπειρο. Έτσι, κατέληξε ο Ζήνων, ότι ο Αχιλλέας δε θα φτάσει ποτέ τη χελώνα. Δηλαδή συμπεραίνουμε  ότι «ο ταχύτερος ποτέ δεν θα προσπεράσει τον βραδύτερο».

Όμως σήμερα ξέρουμε ότι ο συνολικός χρόνος που χρειάζεται ο Αχιλλέας είναι ένας πεπερασμένος αριθμός και δίνεται απ’ τη σχέση