Ανδρέας Ιωάννου Κασσέτας

η ΓΛΩΣΣΑ.

Με λέξεις της καθημερινής μας ζωής η ΤΑΛΑΝΤΩΣΗ είναι μία κίνηση «πηγαινέλα».

H μπίλια, λόγου χάριν, που πηγαινοέρχεται. Μετακινείται ίσια προς μία κατεύθυνση και επιστρέφει. Πέρα δώθε, πέρα δώθε, πέρα δώθε, «παγιδευμένη» σε μια περιοχή του χώρου και, είτε αυτό γίνεται αργά είτε πιο γρήγορα, πάντως πηγαινοέρχεται. Κάνει ένα «πηγαινέλα» σε ορισμένο χρόνο και αυτό επαναλαμβάνεται.

η ΕΜΠΕΙΡΙΑ. Τα γεγονότα και τα υλικά αντικείμενα

Σε ώρα μαθήματος. Ένα τεντωμένο σκοινί πηγαινοέρχεται με φόντο τον πρασινοπίνακα και με τη μία του άκρη στερεωμένη κάπου ψηλά. Στην άλλη άκρη, η καθηγήτρια, έχει προσδέσει ένα σιδερένιο σφαιρίδιο, έχει ενεργοποιήσει το σφαιρίδιο και το σύστημα αιωρείται και οι μαθητές καλούνται να παρακολουθήσουν την κίνηση

του σφαιριδίου. Με ένα σχετικά ακριβές χρονόμετρο, ένας μαθητής χρονομέτρης διαπιστώνει ότι οι πρώτες αιωρήσεις είναι ισόχρονες με τις επόμενες.

Σε ώρα μαθήματος. Ένα ελατήριο. Στην άκρη του κρεμασμένο ένα βαρίδι και το άλλο του ελατηρίου στερεωμένο λίγο πιο ψηλά . Η καθηγήτρια ενεργοποιεί το βαρίδι προδίδοντάς μία κατακόρυφη ταχύτητα και καλεί τους μαθητές να αφουγκραστούν την παλινδρομική κίνηση. Με ένα σχετικά ακριβές χρονόμετρο, ένας μαθητής χρονομέτρης διαπιστώνει

ότι οι κατακόρυφες παλινδρομικές κινήσεις ολοκληρώνονται, όλες σε ίσους χρόνους.

Σε ώρα μαθήματος. Ένα οριζόντια τοποθετημένο ελατήριο στο τραπέζι του εργαστηρίου.

Το ένα του άκρο στερεωμένο σε κατακόρυφο στέλεχος και στο άλλο του άκρο ένα μεταλλικό σφαιρίδιο. Η καθηγήτρια ενεργοποιεί το σφαιρίδιο προσδίδοντάς του οριζόντια ταχύτητα κατά τον άξονα του ελατηρίου και οι μαθητές παρακολουθούν την οριζόντια παλινδρομική κίνησή του. Με ένα σχετικά ακριβές χρονόμετρο, μια μαθήτρια διαπιστώνει

ότι τα χρονικά διαστήματα για την ολοκλήρωση κάθε οριζόντιας παλινδρόμησης είναι ίσα μεταξύ τους.

Και δεν είναι μόνον αυτό.

Οι πιο ευαίσθητοι από τους μαθητές κατά την εξέλιξη των τριών αυτών κινήσεων

αφουγκράζονται μία «κρυμμένη» ΑΡΜΟΝΙΑ.

η ΣΚΕΨΗ. Από τα γεγονότα στις έννοιες

Πίσω από τη διαφορετικότητα των τριών φαινομένων η Σκέψη μας μπορεί, κατ΄ αρχήν, να διακρίνει ομοιότητες. Πρόκειται για τρεις «ευθύγραμμες» παλινδρομικές κινήσεις που επαναλαμβάνονται ανά ίσους χρόνους. Καθεμιά τους είναι μία ΤΑΛΑΝΤΩΣΗ.

Για να μελετήσουμε το φαινόμενο από θεωρητική σκοπιά κάνουμε αυτό που κάνουν οι φυσικοί . Χρησιμοποιούμε ΕΝΝΟΙΕΣ της Γεωμετρίας και της Φυσικής, δοκιμασμένες σε άλλα φαινόμενα. Για το συγκεκριμένο φαινόμενο οι έννοιες αυτές μπορούν να ομαδοποιηθούν σε :

1. ΈΝΝΟΙΕΣ όπως η «ΥΛΙΚΟ ΣΗΜΕΙΟ», και η ΕΥΘΥΓΡΑΜΜΗ ΤΡΟΧΙΑ απαιτούμενες για τον προσδιορισμό του φαινομένου και στη συνέχεια

2. ΕΝΝΟΙΕΣ, όπως η «ΣΥΣΤΗΜΑ ΑΝΑΦΟΡΑΣ και η ΤΑΧΥΤΗΤΑ, απαιτούμενες για την ΠΕΡΙΓΡΑΦΗ του στη γλώσσα της Φυσικής και τέλος

3. ΕΝΝΟΙΕΣ , όπως η ΔΥΝΑΜΗ και η ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ , απαιτούμενες για την ΕΡΜΗΝΕΙΑ του στη γλώσσα πάντοτε της Φυσικής.

Το μοντέλο ΥΛΙΚΟ ΣΗΜΕΙΟ.

Από τη σκοπιά της εμπειρικής προσέγγισης το φαινόμενο αναφέρεται σε υλικό αντικείμενο το οποίο θα μπορούσε να είναι ένα σφαιρίδιο, κάποιο βαρίδι ή ένα οποιοδήποτε στερεό αντικείμενο.

Για να μελετήσουν το φαινόμενο οι φυσικοί – από την εποχή του Isaac Newton – αντί για το υλικό αυτό αντικείμενο «βλέπουν» ένα σώμα-μοντέλο το λεγόμενο ΥΛΙΚΟ ΣΗΜΕΙΟ, ένα αντικείμενο δηλαδή με αδράνεια, τις διαστάσεις του οποίου μπορούμε να τις αγνοήσουμε.

Σε γλώσσα λιγότερο συμβατική μπορούμε να πούμε ότι το ΥΛΙΚΟ αυτό ΣΗΜΕΙΟ «κατοικεί» μόνιμα ή στιγμιαία σε κάποιο ΓΕΩΜΕΤΡΙΚΟ ΣΗΜΕΙΟ, η θέση του οποίου είναι και θέση του ΥΛΙΚΟΥ ΣΗΜΕΙΟΥ και προσδιορίζεται σε σχέση με κάποιο ΣΥΣΤΗΜΑ ΑΝΑΦΟΡΑΣ.

Το σχετικό διάνυσμα που αντιστοιχεί στην αρχή των αξόνων και στο ΓΕΩΜΕΤΡΙΚΟ ΣΗΜΕΙΟ λέγεται POSITION και στην ελληνική απόδοση ΘΕΣΗ ή απομάκρυνση.

Το ΦΑΙΝΟΜΕΝΟ.

Το φαινόμενο «ανήκει», αφενός μεν, στην οικογένεια των ΠΕΡΙΟΔΙΚΩΝ ΦΑΙΝΟΜΕΝΩΝ αφετέρου δε, στη μεγάλη οικογένεια των φαινομένων ΚΙΝΗΣΗΣ.

Πρόκειται λοιπόν για ΠΕΡΙΟΔΙΚΗ ΚΙΝΗΣΗ, χαρακτηριζόμενη από περίοδο και συχνότητα, και ακόμα πιο συγκεκριμένα για μία ειδικού ενδιαφέροντος ΠΑΛΙΝΔΡΟΜΙΚΗ ΠΕΡΙΟΔΙΚΗ ΚΙΝΗΣΗ (ΤΑΛΑΝΤΩΣΗ ) η εξέλιξη της οποίας συντελείται με μία αρμονία.

Το φαινόμενο, βέβαια, το οποίο μπορούμε θεωρητικά – με τη βοήθεια των εννοιών και της μαθηματικής ανάλυσης – να μελετήσουμε είναι η ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ η οποία εκτός του ότι αναφέρεται στο μοντέλο ΥΛΙΚΟ ΣΗΜΕΙΟ είναι και η ίδια ένα ΜΟΝΤΕΛΟ, ένα φαινόμενο δηλαδή το οποίο δεν ταυτίζεται με την εμπειρική του θεώρηση μολονότι , σε ορισμένες περιπτώσεις, προσεγγίζεται από αυτήν.

Είναι ΚΙΝΗΣΗ υλικού σημείου

Είναι ΠΕΡΙΟΔΙΚΗ ΚΙΝΗΣΗ υλικού σημείου

Είναι ΠΑΛΙΝΔΡΟΜΙΚΗ ΠΕΡΙΟΔΙΚΗ ΚΙΝΗΣΗ υλικού σημείου δηλαδή ΤΑΛΑΝΤΩΣΗ

Είναι ΕΥΘΥΓΡΑΜΜΗ ΤΑΛΑΝΤΩΣΗ υλικού σημείου

και ειδικότερα

Είναι ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ, μία δηλαδή ΕΥΘΥΓΡΑΜΜΗ ΤΑΛΑΝΤΩΣΗ υλικού σημείου η θέση του οποίου, κατά το κύλημα του χρόνου, μεταβάλλεται αρμονικά. Αυτό, στη γλώσσα των μαθηματικών, σημαίνει ότι οι η συνάρτηση θέσης - χρόνου είναι ημιτονοειδής.

Το ότι θα μελετήσουμε το συγκεκριμένο φαινόμενο σημαίνει ότι

α. θα το ΠΕΡΙΓΡΑΨΟΥΜΕ και στη συνέχεια

β. θα το ΕΡΜΗΝΕΥΣΟΥΜΕ, θα ερευνήσουμε δηλαδή τις προϋπόθεσης που απαιτούνται ώστε να συμβεί.

η ΠΕΡΙΓΡΑΦΗ ( Οι ΕΝΝΟΙΕΣ, Τα ερωτήματα και η ΑΛΓΕΒΡΑ, Η ΓΕΩΜΕΤΡΙΑ της περιγραφής )

α. Οι ΕΝΝΟΙΕΣ για την περιγραφή

Εφόσον το φαινόμενο είναι ΚΙΝΗΣΗ υλικού σημείου οι έννοιες που χρειαζόμαστε για την περιγραφή του είναι

η ΧΡΟΝΙΚΗ ΣΤΙΓΜΗ ( για τον προσδιορισμό της οποίας χρειαζόμαστε τις έννοιες ΧΡΟΝΙΚΗ ΔΙΑΡΚΕΙΑ και ΧΡΟΝΙΚΟ ΣΥΣΤΗΜΑ ΑΝΑΦΟΡΑΣ)

η ΤΡΟΧΙΑ,

το ΧΩΡΙΚΟ ΣΥΣΤΗΜΑ ΑΝΑΦΟΡΑΣ (το οποίο συνήθως το ξεχνάμε, λες και είναι δυνατόν να περιγράψουμε και να ερμηνεύσουμε μια οποιαδήποτε κίνηση αγνοώντας το χωρικό σύστημα αναφοράς )

και τα διανυσματικά μεγέθη

ΘΕΣΗ,

ΤΑΧΥΤΗΤΑ και

ΕΠΙΤΑΧΥΝΣΗ

Εφόσον είναι ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ μπορούμε να χρησιμοποιούμε ένα κατάλληλο ΣΥΣΤΗΜΑ ΑΝΑΦΟΡΑΣ, έτσι ώστε ή ευθεία του άξονα x να μην είναι μία τυχαία ευθεία αλλά να συμπίπτει με την τροχιά. Με αυτή την προϋπόθεση τα διανύσματα ΘΕΣΗ, ΤΑΧΥΤΗΤΑ και ΕΠΙΤΑΧΥΝΣΗ θα βρίσκονται στον άξονα κα μπορούμε να τα προσδιορίζουμε μόνο με τις αλγεβρικές τιμές τους. Η αλγεβρική τιμή κάθε διανυσματικού μεγέθους είναι το μέτρο του με πρόσημο καθοριζόμενο από τη φορά του αντίστοιχου διανύσματος σε σχέση με συμφωνημένο άξονα.

Εφόσον είναι ΕΥΘΥΓΡΑΜΜΗ ΤΑΛΑΝΤΩΣΗ, παλινδρομική δηλαδή κίνηση που λαμβάνει χώρα εκατέρωθεν μιας θέσης ( την συμβολίζουμε με 0) , μπορούμε να τοποθετήσουμε έτσι τον άξονα x ώστε η αρχή των αξόνων να βρίσκεται σε αυτή τη θέση. Η θέση αυτή είναι ένα σημαντικό ΓΕΩΜΕΤΡΙΚΟ ΣΗΜΕΙΟ τόσο για την περιγραφή όσο και την ερμηνεία της κίνησης και λέγεται ΘΕΣΗ ΙΣΟΡΡΟΠΙΑΣ.

Εφόσον, τέλος, είναι ΠΕΡΙΟΔΙΚΗ ΚΙΝΗΣΗ περιγράφεται και με τις έννοιες ΠΕΡΙΟΔΟΣ και ΣΥΧΝΟΤΗΤΑ.

β. Τα ΕΡΩΤΗΜΑΤΑ και η ΑΛΓΕΒΡΑ

Κατά την περιγραφή του φαινομένου θα αδιαφορήσουμε για το εάν και πώς ο αρμονικός ταλαντωτής αλληλεπιδρά με το υπόλοιπο Σύμπαν, θα συμφωνήσουμε στο «ποια στιγμή θα θεωρήσουμε ως αρχή των χρόνων» και θα αναζητήσουμε απαντήσεις στα τρία βασικά ερωτήματα σχετικά με το κινούμενο αντικείμενο

α. « που θα βρίσκεται (ποια θα είναι η θέση του ) ο αρμονικός ταλαντωτής σε κάθε στιγμή στο μέλλον;»

β. « ποιος θα είναι ο ρυθμός μεταβολής της θέσης του (η ταχύτητά του ) σε κάθε στιγμή στο μέλλον;» και

γ. «ποιος θα είναι ο ρυθμός μεταβολής της ταχύτητάς του (η επιτάχυνσή του ) σε κάθε στιγμή στο μέλλον;».

Και στο ερώτημα αυτό θα σταματήσουμε. Δεν θα αναζητήσουμε δηλαδή και μια απάντηση στο ερώτημα « ποιος θα είναι ο ρυθμός μεταβολής της επιτάχυνσής του;»

Με δεδομένο το ότι η αρμονική ταλάντωση είναι μία κίνηση ΕΥΘΥΓΡΑΜΜΗ, η απάντηση σε καθένα από τα τρία ερωτήματα δίδεται με μία σχέση με χαρακτήρα αλγεβρικής συνάρτησης, η οποία , όπως συμβαίνει με ανάλογες σχέσεις στη Φυσική, μπορεί να χρησιμοποιηθεί και ως εξίσωση με ένα άγνωστο.

Ας συμφωνήσουμε να επιλέξουμε ως αρχή των χρόνων μία χρονική στιγμή κατά την οποία το αντικείμενο βρίσκεται στη θέση ισορροπίας κινούμενο προς τον θετικό ημιάξονα.

Η απάντηση στο πρώτο ερώτημα δίδεται με την x = Aημωt,

η οποία συνιστά και την «εξίσωση ορισμού» του φαινομένου ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ.

Στη συνάρτηση αυτή εμφανίζονται δύο μεταβλητές και δύο σταθερές. Η μεταβλητή x παριστάνει την αλγεβρική τιμή της θέσης (ή απομάκρυνσης, όπως έχει παραδοσιακά και ανεξήγητα επικρατήσει σε ένα μέρος της ελληνικής βιβλιογραφίας) και η μεταβλητή t που παριστάνει τη χρονική στιγμή για την οποία ισχύει η απάντηση στο τεθέν ερώτημα.

Η συμβολιζόμενη με Α σταθερά , είναι θετική ποσότητα με διαστάσεις μήκους για την οποία μπορεί κανείς να διακρίνει ότι παριστάνει τη μέγιστη απόσταση του κινητού από τη θέση ισορροπίας. Χαρακτηρίζεται ως ΠΛΑΤΟΣ ΤΗΣ ΤΑΛΑΝΤΩΣΗΣ.

Τέλος η σταθερά ω αποτελεί συντομογραφία του γινομένου της συχνότητας επί τον αριθμό 2π και λέγεται κυκλική ( ή γωνιακή ) συχνότητα.

Αν θέλετε κάνετε κλικ στο και θα βρεθείτε μπροστά σε ένα animation με τρία αντικείμενα που εκτελούν κατακόρυφες αρμονικές ταλαντώσεις με το ίδιο πλάτος αλλά με διαφορετικές συχνότητες. Θα δείτε επίσης να διαγράφεται η γραφική παράσταση της θέσης κάθε αντικειμένου σε συνάρτηση με το χρόνο.

Αξίζει να παρατηρήσουμε ότι στις κινήσεις που θα παρατηρήσουμε η x = Aημωt δεν έχει τη μορφή αυτή διότι ως αρχή των χρόνων έχει επιλεγεί μία χρονική στιγμή που κανένα από τα τρία αντικείμενα δεν βρίσκεται στη θέση ισορροπίας.

Από την προηγούμενη σχέση x = Aημωt και σε συνδυασμό με την εξίσωση ορισμού της ταχύτητας (υ=dx/dt) προκύπτει η υ= ωΑσυνωt η οποία αποτελεί την σε αλγεβρική γλώσσα απάντηση στο δεύτερο ερώτημα για την ταχύτητα. Στη συνάρτηση αυτή η μεταβλητές είναι η t που παριστάνει τη χρονική στιγμή για την οποία ισχύει η απάντηση και η υ η οποία παριστάνει την αλγεβρική τιμή της ταχύτητας, μία δηλαδή φυσική ποσότητα με διαστάσεις ταχύτητας που μπορεί να είναι θετική ή αρνητική ανάλογα με τη φορά της στιγμιαίας ταχύτητας σε σχέση πάντα με τον άξονα x του συστήματος αναφοράς. Όσο για τις σταθερές, αυτές είναι ίδιες με εκείνες της πρώτης συνάρτησης.

Από τη σχέση υ= ωΑσυνωt και σε συνδυασμό με την εξίσωση ορισμού της επιτάχυνσης (α=dυ/dt) προκύπτει η a = -ω²Αημωt η οποία αποτελεί την σε αλγεβρική γλώσσα απάντηση στο τρίτο ερώτημα για την επιτάχυνση. Και εδώ κατά ανάλογο με τα προηγούμενα τρόπο η α παριστάνει την αλγεβρική τιμή της επιτάχυνσης , μία δηλαδή φυσική ποσότητα με διαστάσεις επιτάχυνσης που μπορεί να είναι θετική ή αρνητική ανάλογα με τη φορά της στιγμιαίας επιτάχυνσης σε σχέση πάντα με τον άξονα x του συστήματος αναφοράς.

Αυτά όλα σημαίνουν ότι οι αλγεβρικές τιμές της θέσης, της ταχύτητας και της επιτάχυνσης, οι οποίες έχουν νόημα μόνο σε σχέση με τον άξονα x του συστήματος αναφοράς, μας δίδουν πληροφορία τόσο για τα μέτρα των διανυσμάτων θέση, ταχύτητα και επιτάχυνση όσο και για τη φορά κάθε διανύσματος, μας δίδουν με άλλα λόγια μία πλήρη απάντηση σε καθένα από τα τρία ερωτήματα.

Οι συναρτήσεις βέβαια αυτές ισχύουν μόνο εφόσον κατά τη χρονική στιγμή που θεωρήθηκε ως Αρχή των χρόνων το κινούμενο αντικείμενο βρισκόταν στη θέση x=0 και η ταχύτητά είχε θετική τιμή.

Εφόσον δεν ισχύει αυτή η προϋπόθεση οι σχέσεις θα έχουν αντίστοιχα τη μορφή

x= Aημ(ωt+φ) υ= ωΑσυν(ωt+φ) a = -ω²Αημ(ωt+φ)

Ο συνδυασμός της πρώτης από τις σχέσεις με την τρίτη) μας δίνει την ΙΔΙΑΙΤΕΡΑ ΣΗΜΑΝΤΙΚΗ για το φαινόμενο σχέση α = - ω²x

Η σχέση αυτή «μας λέει» - κάτι ιδιαίτερα σημαντικό για την εξέλιξη του φαινομένου - ότι

η επιτάχυνση του αντικειμένου έχει διαρκώς αντίθετο πρόσημο από την απομάκρυνση

ή , ισοδύναμα, ότι

Η ΕΠΙΤΑΧΥΝΣΗ ΚΑΤΕΥΘΥΝΕΤΑΙ ΠΑΝΤΟΤΕ ΠΡΟΣ ΤΗ ΘΕΣΗ ΙΣΟΡΡΟΠΙΑΣ

γ. Η ΓΕΩΜΕΤΡΙΑ της περιγραφής

ΤΡΙΑ ΓΕΩΜΕΤΡΙΚΑ ΣΗΜΕΙΑ ΙΔΙΑΙΤΕΡΗΣ ΣΗΜΑΣΙΑΣ

Η Γεωμετρία της περιγραφής περιλαμβάνει

Τον άξονα x, η ευθεία του οποίου συμπίπτει με την τροχιά

την ευθεία της τροχιάς,

το ευθύγραμμο τμήμα της ΑΑ΄ στο οποίο «περιορίζεται» η κίνηση και τα γεωμετρικά σημεία του τμήματος στα θα βρίσκεται το κινούμενο αντικείμενο.

Τρία από τα ΓΕΩΜΕΤΡΙΚΑ αυτά ΣΗΜΕΙΑ παρουσιάζουν ιδιαίτερο ενδιαφέρον.

Τα δύο από αυτά είναι τα άκρα Α και Α΄ του τμήματος στο οποίο περιορίζεται η απλή αρμονική ταλάντωση. Η ιδιαιτερότητά τους έγκειται στο ότι όταν το κινούμενο σώμα βρεθεί στα ΓΕΩΜΕΤΡΙΚΑ αυτά ΣΗΜΕΙΑ, η ταχύτητά του είναι βέβαια αυτονόητα μηδενική αλλά τόσο η επιτάχυνση όσο και η ασκούμενη στον σώμα ( συνισταμένη ) δύναμη έχουν τη μεγαλύτερη κατά μέτρο τιμή τους. Μέγιστη είναι επίσης και η τιμή της δυναμικής ενέργειας του ταλαντωτή.

Ακόμα μεγαλύτερο ενδιαφέρον εμφανίζει το μέσον του ΑΑ΄ το λεγόμενο και ΘΕΣΗ ΙΣΟΡΡΟΠΙΑΣ, στο οποίο, για λόγους απλούστευσης, τοποθετούμε και την Αρχή των αξόνων, και κατά συνέπεια από το σημείο αυτό μετράμε τη θέση ( απομάκρυνση ) x. Το ΓΕΩΜΕΤΡΙΚΟ αυτό ΣΗΜΕΙΟ συμβολίζεται με το γράμμα όμικρον ή με το μηδέν. Τη στιγμή κατά την οποία ο αρμονικός ταλαντωτής διέρχεται από αυτό έχει τη μεγαλύτερη – κατά μέτρο- ταχύτητα. Εφόσον ο αρμονικός ταλαντωτής βρίσκεται στο ΓΕΩΜΕΤΡΙΚΌ αυτό ΣΗΜΕΙΟ – είτε κινούμενο είτε ακίνητος - είναι μηδενική τόσο η επιτάχυνση του κινούμενου ταλαντωτή όσο και η συνισταμένη των ασκουμένων σε αυτόν δυνάμεων. Με άλλα λόγια όταν ο αρμονικός ταλαντωτής βρίσκεται στη θέση ισορροπίας ΟΙ ΑΣΚΟΥΜΕΝΕΣ ΣΕ ΑΥΤΟΝ ΔΥΝΑΜΕΙΣ ΙΣΟΡΡΟΠΟΥΝ, εξ ου και ο όρος «ΘΕΣΗ ΙΣΟΡΡΟΠΙΑΣ». Ιδιαίτερη τέλος σημασία πρέπει να δώσουμε στο γεγονός ότι « ο ταλαντωτής στη θέση ισορροπίας έχει τη λιγότερη δυναμική ενέργεια σε σχέση με οποιαδήποτε άλλη θέση». Κι αυτό ανεξάρτητα από το αν είναι κινείται ή είναι ακίνητος.

δ. Η ΑΝΑΛΥΤΙΚΗ ΓΕΩΜΕΤΡΙΑ της Περιγραφής

Στην αλγεβρική συνάρτηση x = Aημωt, η οποία αποτελεί την αλγεβρική απάντηση στο ερώτημα «που θα βρίσκεται το κινούμενο αντικείμενο;» αντιστοιχεί και μία ΕΙΚΟΝΑ, η γραφική παράσταση της συνάρτησης, η απάντηση της Αναλυτικής Γεωμετρίας.

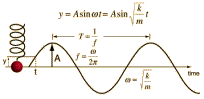Στην εικόνα, για την αλγεβρική τιμή της θέσης, χρησιμοποιείται το σύμβολο y

και για το συμβολισμό του ημιτόνου το διεθνές sin.

Αντίστοιχες ΕΙΚΟΝΕΣ μπορούν να χρησιμοποιηθούν για τις συναρτήσεις υ= ωΑσυν και α= - ω²Aημωt,

Αν κάνετε ΚΛΙΚ στο κόκκινο τόξο

θα βρεθείτε σε μία σελίδα, την 1, με συνοπτικές σημειώσεις τις οποίες μπορείτε να χρησιμοποιήσετε κατά τη διδασκαλία σας σε μαθητές Λυκείου. Μπορείτε να την αξιοποιήσετε ως διαφάνεια είτε να τη δώσετε σε φωτοαντίγραφα στους μαθητές σας

η ΕΡΜΗΝΕΙΑ του φαινομένου

Οι έννοιες

Το βασικό ερώτημα σχετικά με την ερμηνεία του φαινομένου είναι :

«Τι συμβαίνει κατά την αλληλεπίδραση ενός σώματος με το υπόλοιπο Σύμπαν και υποχρεώνει το σώμα αυτό να εκτελεί αρμονική ταλάντωση;»

Η σχετική έρευνα που θα οδηγήσει στην απάντηση θα αυτή θα γίνει σε δύο «γλώσσες». Πρώτα θα κινηθούμε μέσα

στα πλαίσια της βασικής νευτωνικής παράδοσης στην οποία ρόλο πρωταγωνιστή παίζει η έννοια ΔΥΝΑΜΗ και στη συνέχεια,

στα πλαίσια της θερμοδυναμικής, στην οποία πρωταγωνιστεί η έννοια ΕΝΕΡΓΕΙΑ και ιδιαίτερα η έννοια ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ ΤΑΛΑΝΤΩΤΗ

Αν κάνετε ΚΛΙΚ στη φράση ΝΕΥΤΩΝΙΚΗ ΔΥΝΑΜΙΚΗ θα βρεθείτε σε μία σελίδα , τη 2, με σημειώσεις για την εφαρμογή της Νευτωνικής Δυναμικής στο φαινόμενο ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ τις οποίες μπορείτε να αξιοποιήσετε για τη διδασκαλία σας..

Αν κάνετε ΚΛΙΚ στη φράση ΕΝΕΡΓΕΙΑ ΕΝΟΣ ΤΑΛΑΝΤΩΤΗ θα βρεθείτε σε μία ΆΛΛΗ σελίδα, την 3, με σημειώσεις για την ενέργεια των αρμονικών ταλαντωτών, τις οποίες μπορείτε να αξιοποιήσετε για τη διδασκαλία.

Αν κάνετε ΚΛΙΚ στο κόκκινο τόξο θα βρεθείτε μπροστά σε μία απόπειρα για ΤΗΝ ΟΙΚΟΔΟΜΗΣΗ της έννοιας ΑΡΜΟΝΙΚΟΣ ΤΑΛΑΝΤΩΤΗΣ, η οποία παραδοσιακά «αδικείται» κατά τη διδασκαλία του φαινομένου ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ

Στη Δευτέρα Λυκείου, σύμφωνα με το Πρόγραμμα Σπουδών οι μαθητές διδάσκονται ΓΡΑΜΜΙΚΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ

Στην Τρίτη Λυκείου, σύμφωνα με το Πρόγραμμα Σπουδών, οι μαθητές

διδάσκονται ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ

Τι είναι, τέλος πάντων, η ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ; Απλή; Γραμμική; Και τα δύο;

Και αν το ΑΠΛΗ και το ΑΡΜΟΝΙΚΗ είναι συνώνυμα γιατί επιμένουν στο ΓΡΑΜΜΙΚΗ οι μεν και στο ΑΠΛΗ οι δε και δεν χρησιμοποιούν κάποια παρένθεση; ΑΠΛΗ ( ή ΓΡΑΜΜΙΚΗ) ;

Η ΔΙΚΗ ΜΑΣ ΑΠΟΨΗ

Αν ,τέλος, θέλετε να συναντήσετε ένα από το κλασικά animations με το οποίο, χιλιάδες καθηγητές και μαθητές σε όλο τον Κόσμο, «απολαμβάνουν», μέσα από διεργασίες «interactive», γεγονότα αρμονικής ταλάντωσης θα χρειαστεί να κάνετε ΚΛΙΚ στο

Επιστροφή στην κεντρική σελίδα ΔΙΔΑΚΤΙΚΗ ΤΗΣ ΦΥΣΙΚΗΣ

.