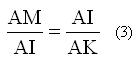Διπλασιασμός του κύβου  -   Η λύση  του Αρχύτα

 
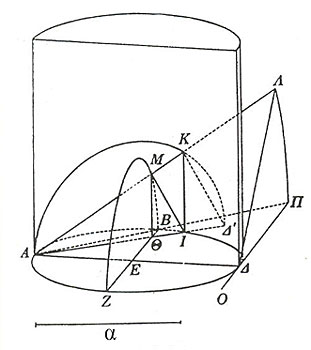Η  λύση  του Αρχύτα, στο πρόβλημα του διπλασιασμού του κύβου, περιγράφεται από τον Ευτόκιο ο οποίος πήρε στοιχεία από τον Εύδημο και έχει ως εξής.
 

Γράφουμε ένα κύκλο διαμέτρου  ΑΔ=2α,  όπου   α  η πλευρά του κύβου  που θέλουμε να διπλασιάσουμε  και παίρνουμε μια χορδή  του  ΑΒ=α .

Φέρουμε  την εφαπτομένη του κύκλου  στο σημείο του Δ  και έστω ότι τέμνει την  ΑΒ  στο  Π.

Φέρουμε την ΒΕΖ  παράλληλη  στην  ΠΔ. Θεωρούμε  ένα ορθό ημικύλινδρο με βάση το ημικύκλιο ΑΒΔ  και ένα ορθό ημικύκλιο με διάμετρο την ΑΔ  κάθετο  στο επίπεδο του κύκλου ΑΒΔΖ. Όταν το ημικύκλιο αυτό περιστρέφεται από το Δ προς το Β, παραμένοντας πάντα κάθετο στο επίπεδο της βάσης και το άκρο του Α να είναι σταθερό, θα τέμνει την κυλινδρική επιφάνεια και θα γράφει σε αυτή μια γραμμή, έστω  C ( στο σχήμα δεν υπάρχει). Εξάλλου αν η  ΑΔ παραμένει σταθερή και το τρίγωνο ΑΠΔ περιστραφεί γύρω από την ΑΔ  και  αντίθετα από το ημικύκλιο, τότε η  ΑΠ  θα γράψει μια κωνική επιφάνεια  και ταυτόχρονα το σημείο Β θα γράψει πάνω στην κωνική επιφάνεια

ένα ημικύκλιο. Η κωνική αυτή επιφάνεια θα τμήσει την καμπύλη  C σε ένα σημεία Κ και  έστω ότι τότε:

·        Το τρίγωνο ΑΠΔ  έχει τη θέση ΑΛΔ

·        Η  ΑΚΛ  τέμνει το ημικύκλιο που γράφει το Β  στο Μ,  το ημικύκλιο αυτό είναι το  ΒΜΖ.

·        το ημικύκλιο που γράφει την καμπύλη C  έχει τη θέση ΑΚΔ΄.

Από το  σημείο  Κ  φέρουμε μια κάθετο στο επίπεδο  ΑΒΔ  η οποία τέμνει τον κύκλο ΑΒΔΖ διότι ο κύλινδρος είναι ορθός ,έστω  ΚΙ  η κάθετος αυτή. Φέρουμε την ΑΙ  η οποία τέμνει την ΒΖ  στο Θ.

Η  ΜΘ είναι η κοινή τομή των ημικυκλίων ΑΚΔ΄ και  ΒΜΖ  τα οποία είναι κάθετα στον κύκλο της βάσης ,άρα και η ΜΘ είναι κάθετη σ’ αυτόν, άρα και στην ΒΖ ( και στην ΑΙ)  δηλ είναι ύψος στο ορθογώνιο τρίγωνο ΒΜΖ  άρα ισχύει 

                                                                    

Η δύναμη του σημείου Θ ως προς τον κύκλο ΑΒΔΖ  δίνει τη σχέση   

 και λόγω της (1) θα είναι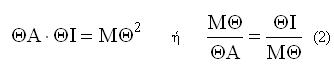                   

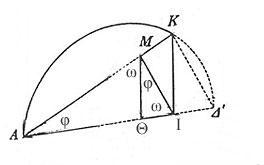Λόγω  της  (2)  και επειδή η ΜΘ είναι κάθετη στην ΑΙ  τα τρίγωνα  ΜΘΙ   και  ΘΑΜ  είναι όμοια  και οι γωνίες που έχουμε ονομάσει  ίσες ( στο διπλανό σχήμα), άρα η γωνία ΑΜΙ  είναι ορθή. Έτσι  στο διπλανό σχήμα  τα ορθογώνια τρίγωνα ΑΜΙ και ΑΙΚ είναι όμοια με τις γωνίες ΑΙΜ και ΑΚΙ ίσες αφού ΜΘ//ΚΙ ,  άρα         

Επίσης τα τρίγωνα ΚΑΙ  και  ΚΑΔ΄ είναι όμοια με τις γωνίες ΑΚΙ   και ΑΔ΄Κ  ίσες, ως ίσες με την  ω  λόγω των ΚΙ//ΜΘ  και ΚΔ΄// ΜΙ,  άρα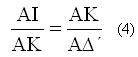       

Από τις  (3)  και (4)  προκύπτει        

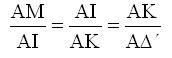
και επειδή  ΑΜ=ΑΒ= α ( ως γενέτειρες του κώνου με κορυφή το Α και βάση το ημικύκλιο ΒΜΖ)   και  ΑΔ΄=2α  έχουμε 

                                                          

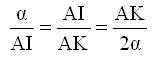
και θέτοντας   x= AI  και  y= AK  η τελευταία γίνεται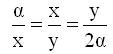        

δηλ  προκύπτει  η αναλογία του Ιπποκράτη.  Άρα  το τμήμα  ΑΙ  είναι η πλευρά του διπλάσιου κύβου.

 
Βιβλιογραφία
 

Κεντρική σελίδα  

 

Η λύση του : Αρχύτα ,  Ευδόξου , Μεναίχμου,  Πλάτωνα , Ερατοσθένη, Νικομήδη, Απολλωνίου, Ήρωνα,
                 Διοκλή, Πάππου,  Descartes