Διπλασιασμός του κύβου -Η λύση του Μεναίχμου
Η λύση του Μεναίχμου στο πρόβλημα του διπλασιασμού του κύβου περιγράφεται από τον Ευτόκιο και είναι η παρακάτω.
Όπως ξέρουμε για να λυθεί το πρόβλημα αρκεί να κατασκευασθούν τα τμήματα x και y της αναλογίας του Ιπποκράτη δηλ. της 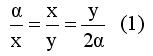 .
.
Από τους δύο πρώτους λόγους της (1) προκύπτει ότι τα τμήματα x και y , ικανοποιούν τη σχέση 
ενώ από τον πρώτο και τον τρίτο την 
και από τους δύο τελευταίους την 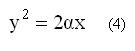 .
.
Αν τα τμήματα x και y θεωρηθούν συντεταγμένες ενός σημείου, τότε λόγω της (2) το σημείο αυτό θα ανήκει σε μία παραβολή και λόγω της (3) σε μία υπερβολή, άρα το σημείο αυτό κατασκευάζεται ως τομή των δύο αυτών γραμμών. Αν αντί της (3) θεωρήσουμε την (4) θα ανήκει πάλι σε μία παραβολή.
Έτσι για να λύσουμε το πρόβλημα του διπλασιασμού του κύβου, κατασκευάζουμε τις παραπάνω καμπύλες, βρίσκουμε το σημείο τομής τους και παίρνουμε την τετμημένη του .Η όλη διαδικασία φαίνεται στην παρακάτω εφαρμογή.