ΕΝΗΜΕΡΩΣΗ-ΨΥΧΑΓΩΓΙΑ-ΕΚΠΑΙΔΕΥΣΗ

Μια έξυπνη απόδειξη του Πυθαγορείου Θεωρήματος με νερό...

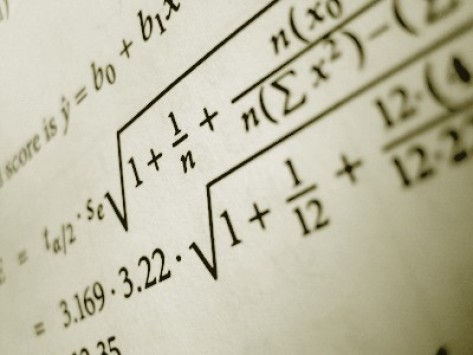Είναι μια εξίσωση ικανή να «λύσει» το πρόβλημα της εγκληματικότητας; Μη βγάλετε μολύβι και χαρτί. Δε μιλάμε για απλή μαθηματική εξίσωση...

Μοιάζει απίστευτο, ίσως ακόμη κι εκτός πραγματικότητας. Σύμφωνα όμως με Αμερικανούς επιστήμονες είναι πέρα για πέρα δυνατό. Ομάδα μαθηματικών κι άλλων επιστημόνων του πανεπιστημίου του Λος Άντζελες (UCLA) ανέπτυξε ένα μαθηματικό - στατιστικό μοντέλο, το οποίο φιλοδοξεί να προβλέψει σε ποιά σημεία θα «χτυπήσουν» οι κλέφτες.

Οι ερευνητές, με επικεφαλής τον Στιβ Κάντρελ, που δημοσίευσαν τη σχετική μελέτη στο περιοδικό μαθηματικής ανάλυσης της Εταιρίας Βιομηχανικών και Εφαρμοσμένων Μαθηματικών "Journal on Mathematical Analysis", αναλύουν χωρικά και χρονολογικά δεδομένα από τις έως τώρα κλοπές σε μία πόλη για να εντοπίσουν «καυτά» σημεία εγκληματικότητας.

Μπορούν έτσι να εκτιμήσουν κατά προσέγγιση σε ποιες περιοχές ή γειτονιές είναι πιθανότερο να συμβούν τα επόμενα κρούσματα κλοπών. Η πρόβλεψη αυτή θα μπορούσε μελλοντικά να βοηθήσει την αστυνομία να επικεντρώσει καλύτερα την αστυνόμευση.

Το νέο μοντέλο πρόβλεψης βασίζεται στην ανάλυση -με μαθηματικά «εργαλεία»- προτύπων και τάσεων σε σειρές δεδομένων, μία δραστηριότητα που μελετάται εδώ και δεκαετίες όχι μόνο στα φυσικά και βιολογικά συστήματα, αλλά και στα κοινωνικά, ώστε να προβλεφθούν μελλοντικές συμπεριφορές και συμβάντα.

Αυτή η αξιοποίηση των μαθηματικών, έχει ενταθεί τελευταία στο πεδίο της επιδεινούμενης εγκληματικότητας, καθώς έχει εμπειρικά παρατηρηθεί ότι οι κλοπές κι άλλες μορφές παράνομων δραστηριοτήτων συγκεντρώνονται σε συγκεκριμένες περιοχές στο χώρο και σε συγκεκριμένες περιόδους στο χρόνο.

Σύγχρονος κατακόρυφος γνώμονας

Ο Γνώμονας είναι ένα από τα αρχαιότερα και απλούστερα επιστημονικά αστρονομικά όργανα. Χρησιμοποιήθηκε από τους αρχαίους λαούς για τη χάραξη της μεσημβρινής γραμμής (διεύθυνση βορρά - νότου), για την εύρεση της χρονικής στιγμής που ο ήλιος μεσουρανεί (αληθής μεσημβρία), για την εύρεση των ισημεριών και των ηλιοστασίων, για την εύρεση της διάρκειας των εποχών και επιπλέον χρησιμοποιήθηκε ως δείκτης των ηλιακών ρολογιών.

Η Γνωμονική είναι κλάδος της αρχαίας αστρονομίας. Μελετά τις ιδιότητες των γνωμόνων, δηλαδή των οργάνων που ρίχνουν τη σκιά τους και ασχολείται με την κατασκευή τους. Στην πάροδο του χρόνου η γνωνονική εξελίχθηκε στην τέχνη κατασκευής ηλιακών ρολογιών. Κύριο μέλημα της γνωμονικής ήταν:

• χάραξη της μεσημβρινής γραμμής
• τοποθέτηση του γνώμονα παράλληλα με τον άξονα της γης
• χάραξη του διαγράμματος των ωρών

Οι αρχαίοι Αιγύπτιοι χρησιμοποιούσαν τον γνώμονα από το 2000 π.Χ.. Ως γνώμονες χρησιμοποιούσαν τους οβελίσκούς, αρκετοί από τους οποίους κοσμούν σήμερα τις πλατείες και τα πάρκα πολλών ευρωπαϊκών μεγαλουπόλεων. Με τη χρήση του γνώμονα οι αρχαίοι Αιγύπτιοι είχαν καταφέρει να προσδιορίσουν τη μεσημβρινή γραμμή (διεύθυνση βορρά - νότου), να μετρήσουν τη φαινόμενη διάμετρο του ήλιου και της σελήνης, και χρησιμοποιώντας τον κατακόρυφο γνώμονα ως ηλιακό ρολόι να μετρούν ώρες άνισης διάρκειας.

Σύμφωνα με τον Ηρόδοτο, οι αρχαίοι Έλληνες γνώρισαν τους γνώμονες από τους Χαλδαίους. Τελειοποίησαν τη χρήση του γνώμονα μιας και είχαν κάνει πολύ μεγάλες προόδους στη γεωμετρία, την τριγωνομετρία και την αστρονομία.
Ο Αναξίμανδρος ο Μιλήσιος (610 -540 π.Χ.) εισήγαγε για πρώτη φορά τη χρήση του γνώμονα στην αρχαία Ελλάδα. Κατασκεύασε έναν πυραμοειδή γνώμονα στην Σπάρτη ο οποίος μπορούσε να δείχνει την αληθή μεσημβρία, τη χρονική στιγμή δηλαδή που μεσουρανεί ο ήλιος.
Ο Αναξιμένης (586-525 π.Χ.) τελειοποίησε τον γνώμονα και κατασκεύασε στην Σπάρτη ένα ηλιακό ρολόι.