Μαθηματικές εξερευνήσεις !!

ΘΕΜΑ Α
A1. Αν η συνάρτηση f είναι παραγωγίσιμη στο ? και c σταθερός πραγματικός αριθμός, να αποδείξετε με τη χρήση του ορισμού της παραγώγου ότι     (cf(x))? = c f? (x),                                                                                                                       Μονάδες 7

A2. Πότε μια συνάρτηση f λέγεται γνησίως φθίνουσα σε ένα διάστημα Δ του πεδίου ορισμού της;     Μονάδες 4

A3. Πότε μια ποσοτική μεταβλητή λέγεται διακριτή και πότε συνεχής;                                                     Μονάδες 4

A4. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας στο τετράδιό σας, δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση, τη λέξη Σωστό, αν η πρόταση είναι σωστή, ή Λάθος, αν η πρόταση είναι λανθασμένη.
α) Αν για τη συνάρτηση f ισχύει f?(x0) = 0, για x0?(α,β), και η παράγωγός της f? διατηρεί πρόσημο εκατέρωθεν του x0, τότε η f είναι γνησίως μονότονη στο (α,β) και δεν παρουσιάζει ακρότατο στο διάστημα αυτό.
(μονάδες 2)

β) Για δύο οποιαδήποτε ενδεχόμενα Α, Β ενός δειγματικού χώρου Ω ισχύει:
P(A – B) = P(B) – P(A ? B)                                                                                                                                        (μονάδες 2)

γ) Σε μια κανονική ή περίπου κανονική κατανομή το 95% περίπου των παρατηρήσεων βρίσκονται στο διάστημα ( ? s, + s) , όπου η μέση τιμή και s η τυπική απόκλιση των παρατηρήσεων.
(μονάδες 2)

δ) Αν xi είναι τιμή μιας ποσοτικής μεταβλητής X, τότε η αθροιστική συχνότητα Ni εκφράζει το πλήθος των παρατηρήσεων που είναι μεγαλύτερες της τιμής xi
(μονάδες 2)

ε) Το κυκλικό διάγραμμα είναι ένας κυκλικός δίσκος χωρισμένος σε κυκλικούς τομείς, τα εμβαδά ή, ισοδύναμα, τα τόξα των οποίων είναι ανάλογα προς τις αντίστοιχες συχνότητες vi ή τις σχετικές συχνότητες fi των τιμών xi της μεταβλητής.
(μονάδες 2)
                                                                                                                                                                                        Μονάδες 10
ΘΕΜΑ Β
Στο παρακάτω σχήμα φαίνεται το ιστόγραμμα συχνοτήτων, το οποίο παριστάνει τις   πωλήσεις σε χιλιάδες ευρώ που έγιναν από τους πωλητές μιας εταιρείας κατά τη διάρκεια ενός έτους.

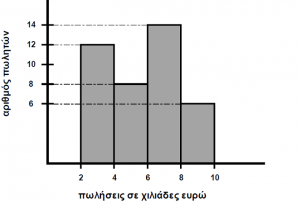
B1. Να βρείτε το πλήθος των πωλητών της εταιρείας.                                                                                        Μονάδες 5
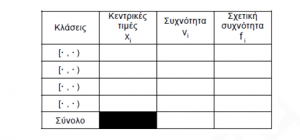
B2. Να μεταφέρετε στο τετράδιό σας τον παρακάτω πίνακα συχνοτήτων της κατανομής των πωλήσεων κατάλληλα συμπληρωμένο, δικαιολογώντας τη στήλη με τις σχετικές συχνότητες fi, i = 1, 2, 3, 4              Μονάδες 8

B3. α) Να υπολογίσετε τη μέση τιμή των πωλήσεων του έτους.                                                                     (μονάδες 6)
β) Να βρείτε το πλήθος των πωλητών που έκαναν πωλήσεις τουλάχιστον 4,5 χιλιάδων ευρώ (θεωρούμε ότι οι παρατηρήσεις κάθε κλάσης είναι ομοιόμορφα κατανεμημένες).                                                                      (μονάδες 6)
Μονάδες 12
ΘΕΜΑ Γ
Ένα δοχείο περιέχει κόκκινες (Κ), άσπρες (Α) και πράσινες (Π) μπάλες. Επιλέγουμε τυχαία μία μπάλα. Η πιθανότητα να προκύψει κόκκινη μπάλα είναι P(Κ) = x1, ενώ η  πιθανότητα να προκύψει άσπρη μπάλα είναι P(Α) = x2, όπου x1, x2 είναι οι θέσεις  των τοπικών ακροτάτων της συνάρτησης , x?? με x1 < x2

Γ1. Να βρείτε τις πιθανότητες P(Κ), P(A) και P(Π), όπου P(Π) η πιθανότητα να προκύψει πράσινη μπάλα.                                                                                                                                                                           Μονάδες 10

Γ2. Αν P(Κ)= και P(A)= , να βρείτε τις πιθανότητες των παρακάτω ενδεχομένων:
Γ: «η μπάλα που επιλέγεται τυχαία να είναι κόκκινη ή άσπρη»
Δ: «η μπάλα που επιλέγεται τυχαία να είναι ούτε κόκκινη ούτε άσπρη»
Ε: «η μπάλα που επιλέγεται τυχαία να είναι άσπρη ή να μην είναι πράσινη».                                                                                                                                                                     Μονάδες 9

Γ3. Αν οι άσπρες μπάλες είναι κατά τέσσερις (4) λιγότερες από τις πράσινες μπάλες, να βρείτε πόσες μπάλες έχει το δοχείο.                                                                                                                                                                         Μονάδες 6
ΘΕΜΑ Δ
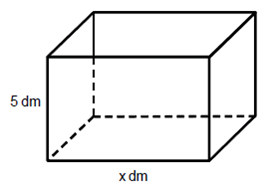
Θεωρούμε ένα κουτί σχήματος ορθογωνίου παραλληλεπιπέδου με βάση ορθογώνιο και ανοικτό από πάνω. Το ύψος του κουτιού είναι 5 dm. Η βάση του κουτιού έχει σταθερή περίμετρο 20 dm και μία πλευρά της είναι x dm με 0<x<10

Δ1. Να αποδείξετε ότι η συνολική επιφάνεια του κουτιού ως συνάρτηση του x είνα

και να βρείτε για ποια τιμή του x το κουτί  έχει μέγιστη επιφάνεια.                                                                                             Μονάδες 8

Στη συνέχεια, θεωρούμε τα σημεία Ai(x i,y i), όπου y i = E(x i) , i = 1, 2,…,15
με 5 = x1< x2< … < x14 < x15 = 9

Δ2. Αν το δείγμα των τετμημένων x i i = 1, 2,…,15 των παραπάνω σημείων Ai(x i,y i)
? δεν είναι ομοιογενές
? έχει μέση τιμή =8 και
? τυπική απόκλιση s τέτοια, ώστε
2s2 – 5s + 2 = 0
τότε:
α) να αποδείξετε ότι s = 2
(μονάδες 4)
β) να βρείτε τη μέση τιμή των , με i = 1, 2,…,15

(μονάδες 4)
Μονάδες 8

Δ3. Επιλέγουμε τυχαία ένα από τα παραπάνω σημεία Ai(x i,y i), i = 1, 2,…,15
Να βρείτε την πιθανότητα του ενδεχομένου:
Β = { Ai(x i,y i), i = 1, 2,…,15 τέτοια, ώστε y i > ? 4xi + 9R + 1}.
όπου R είναι το εύρος των y i = E(x i), i = 1, 2,…,15