 |
από τα Μαθηματικά των Μαθηματικών, των Μαθητών, ... |
|
Μαθηματικά Β΄Γυμνασίου - Εμβαδά Επίπεδων Σχημάτων - Πυθαγόρειο Θεώρημα |
|
|
|
από τα Μαθηματικά των Μαθηματικών, των Μαθητών, ... |
|
Μαθηματικά Β΄Γυμνασίου - Εμβαδά Επίπεδων Σχημάτων - Πυθαγόρειο Θεώρημα |
|
| Περιεχόμενα | ||||||||||
| → | Β-1-1 Φύλλο Εργασίας |
 |
β: Βάση - Μια πλευρά του παραλληλογράμμου υ: Το ύψος που αντιστοιχεί στη βάση β
|
 |
||||||
| → | Εμβαδόν επίπεδης επιφάνειας | |||||||||
| → | Ασκήσεις Β-1-1 | |||||||||
| → | Μονάδες μέτρησης επιφανειών | |||||||||
| → | Ασκήσεις Β-1-2 | |||||||||
| → | Εμβαδόν τετραγώνου | |||||||||
| → | Ασκήσεις Β-1-3α | |||||||||
| → | Εμβαδόν ορθογωνίου | |||||||||
| → | Ασκήσεις Β-1-3β | |||||||||
| → | Εμβαδόν παραλληλογράμμου | |||||||||
| → | Ασκήσεις Β-1-3γ | |||||||||
| → | Εμβαδόν τριγώνου | |||||||||
| → | Ασκήσεις Β-1-3δ | Το εμβαδόν ενός παραλληλογράμμου είναι ίσο με το γινόμενο μιας πλευράς του με το αντίστοιχο σε αυτή ύψος. | ||||||||
| → | Εμβαδόν τραπεζίου | |||||||||
| → | Ασκήσεις Β-1-3ε |
 |
||||||||
| → | Ερωτήσεις κατανόησης Β-1-3 | |||||||||
|
→ |
Β-1-4 Φύλλο Εργασίας | |||||||||
| → | Πυθαγόρειο θεώρημα | |||||||||
| → | Ασκήσεις Β-1-4α |
Αν
 ,  είναι οι μη παράλληλες πλευρές ενός παραλληλογράμμου και
 ,  τα ύψη που αντιστοιχούν σε αυτές, τότε ισχύει η ισότητα:
 |
||||||||
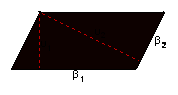
| → | Αντίστροφο Πυθαγορείου θεωρήματος | Στο παραλληλόγραμμο, οι δυο μη παράλληλες πλευρές, μπορούν να θεωρηθούν βάσεις. | ||||||||
| → | Ασκήσεις Β-1-4β | |||||||||
| → | Ασκήσεις επανάληψης | |||||||||
| → | Διάλειμμα | Οι αποστάσεις των απέναντι πλευρών του παραλληλογράμμου είναι τα ύψη του | ||||||||
| Εμβαδόν παραλληλογράμμου java applet | ||||||||||
|
Γιώργος Μαντζώλας - Μελίκη Ημαθίας |
||||||||||
Επικοινωνία
