Πανελλήνιο Σχολικό Δίκτυο Πετρίδης Παντελής
Αρχική σελίδα Σχολείο Σχολική Επιτροπή Από το Γενικό Λύκειο στην Τριτοβάθμια Εκπαίδευση Μαθηματικά Παρατηρήσεις - Σχόλια - Επεκτάσεις σε ασκήσεις Ασκήσεις Τ.Π.Ε. GeoGebra Αρχική Ευθεία y=λx+β - Ερμηνεία των λ,β Τριώνυμο Τριγωνομετρικός κύκλος, αναγωγή στο 1ο τεταρτημόρι Τρίγωνο Γεωμετρία - 3.7 Βασικοί γεωμετρικοί τόποι Σχετικές θέσεις κύκλων Γεωμετρία - §9.7 Τέμνουσες κύκλου - Εφ.2 Κατ.Β' 2.1 Β4 Γεωμετρικοί μετασχηματισμοί Μέτρο αθροίσματος-διαφοράς διανυσμάτων-μιγαδικών Γραφήματα πολυωνύμων (x^n) - ριζών (x^(1/n)) Σύνθεση συναρτήσεων Πολυώνυμο Lagrange 5 σημείων Πολυωνυμική προσέγγιση ελαχίστων τετραγώνων Συμβολή κυμάτων - Σημεία ενίσχυσης και απόσβεσης Συμβολή κυμάτων - Στάσιμα κύματα Διακρότημα - Σύνθεση ταλαντώσεων Σχεδίαση κυκλωμάτων Περιστροφέας! Προγραμματισμός Το πρόβλημα των δύο σοφών Παραπομπές	Πολυώνυμο Lagrange 5 σημείων (4ου βαθμού) Στην εφαρμογή υπάρχουν 5 σημεία και το γράφημα ενός πολυωνύμου (το πολύ) 4ου βαθμού που διέρχεται από αυτά. Μπορείτε να μετακινήσετε τα σημεία αυτά. Θα δείτε ότι το πολυώνυμο προσαρμόζεται έτσι, ώστε να διέρχεται από τα σημεία αυτά διαρκώς*. Η Εφαρμογή GeoGebra δεν μπορεί να εκκινηθεί. Βεβαιωθείτε ότι η έκδοση της Java 1.4.2 (ή νεότερη) έχει εγκατασταθεί και ενεργοποιηθεί στο φυλλομετρητή σας.(Πατήστε εδώ για να εγκαταστήσετε την Java.) Για το πολυώνυμο Lagrange: Έστω ν σημεία του επιπέδου A1(x1,y1), A2(x2,y2), …, Aν(xν,yν)*. Το πολυώνυμο ν-1 βαθμού που περνάει από τα σημεία αυτά είναι το L(x) = y1∙L1(x) + y2∙L2(x) + … + yν∙Lν(x), όπου για κ = 1, 2, …, ν, τα πολυώνυμα Lκ ορίζονται ως εξής: 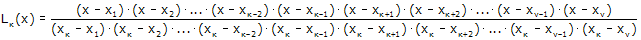Περιγραφικά, το πολυώνυμο Lκ είναι ο λόγος των γινομένων της μορφής x–xi προς τα γινόμενα της μορφής xκ–xi, όπου το i παίρνει όλες τις τιμές από το 1 έως το ν με εξαίρεση το κ. Παρατηρήσεις – Επεξηγήσεις: Αρχικά, παρατηρούμε ότι τα βοηθητικά πολυώνυμα Lκ είναι καλώς ορισμένα*. Επίσης, τα βοηθητικά πολυώνυμα Lκ που χρησιμοποιεί το πολυώνυμο L έχουν την ιδιότητα να μηδενίζονται για όλα τα xi εκτός από το xκ, στο οποίο είναι ίσα με τη μονάδα και, παρά το μεγάλο μέγεθος της παράστασης, μπορούμε εύκολα να το διαπιστώσουμε. Παρατηρήστε ότι ο αριθμητής του Lκ μηδενίζεται για x = x1 επειδή έχει τον παράγοντα x – x1, μηδενίζεται για x = x2 επειδή έχει τον παράγοντα x – x2 κ.ο.κ., ενώ για x = xκ ο αριθμητής γίνεται ίσος με τον παρονομαστή, άρα το κλάσμα ισούται με τη μονάδα. Έτσι, π.χ. είναι L(x1) = y1 διότι για x = x1 τα πολυώνυμα L2, …, Lν μηδενίζονται ενώ το L1 είναι μονάδα. Άρα το γράφημα του L διέρχεται από το Α1 κ.ο.κ. Για το παρόν παράδειγμα: Η παραπάνω εφαρμογή είναι η περίπτωση του πολυώνυμου Lagrange για ν = 5. Επιλέγοντας την επιλογή «LΑ(x)» εμφανίζεται το γράφημα του ομώνυμου βοηθητικού πολυώνυμου, οι προβολές των πέντε σημείων στον x’x, η ευθεία y = 1 και η προβολή του σημείου A πάνω σε αυτήν, ώστε να διαπιστώσετε τον τρόπο που λειτουργεί το πολυώνυμο αυτό (καλύτερα να αποεπιλέξετε την επιλογή «L(x)» για να μην μπερδεύονται τα γραφήματα). Μετακινήστε τα σημεία και πάλι. Θα διαπιστώσετε ότι πράγματι το πολυώνυμο μηδενίζεται στις τετμημένες των Β, Γ, Δ και Ε ενώ γίνεται μονάδα στην τετμημένη του Α. Το πολυώνυμο αυτό εμφανίζεται ως παράδειγμα ενώ ανάλογα λειτουργούν και τα υπόλοιπα πολυώνυμα. * Από τα σημεία αυτά θέλουμε να διέρχεται το γράφημα της συνάρτησης, άρα θα πρέπει να έχουν διαφορετικές τετμημένες ανά δύο. Δημιουργήθηκε με το πρόγραμμα GeoGebra ΔΗΜΟΣΙΕΥΤΗΚΕ: 24/2/2010
Πετρίδης Παντελής, Μαθηματικός - Επικοινωνία: ppetridis@sch.gr - Τελευταία ενημέρωση: 26/6/2013 (/GeoGebra/Μέτρο αθροίσματος-διαφοράς διανυσμάτων-μιγαδικών)