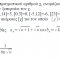Numeri idonei
What are these numeri idonei of Euler? Also called convenient
numbers, they were used conveniently by Euler to produce prime
numbers.
Now I will explain what the numeri idonei are. Let n ≥ 1. If q is an
odd prime and there exist integers x, y ≥ 0 such that q = x2 + ny2 ‚
then:
(i) gcd(x, ny) = 1;
(ii) if q = x1 2 + ny12 with integers x 1 , y 1 ≥ 0, then x = x 1 and y = y 1 .
We may ask the following question. Assume that q is an odd in–
teger, and that q = x 2 + ny 2 , with integers x, y ≥ 0, such that
conditions (i) and (ii) above are satisfied. Is q a prime number?
The answer depends on n. If n = 1, the answer is “yes”, as Fer–
mat knew. For n = 11, the answer is “no”: 15 = 2 2 + 11 · 1 2 and
conditions (i) and (ii) hold, but 15 is composite. Euler called n a
numerus idoneus if the answer to the above question is “yes”.
Euler gave a criterion to verify in a finite number of steps whether
a given number is convenient, but his proof was flawed. Later, in
1874, Grube found the following criterion, using in his proof results
of Gauss, which I will mention soon. Thus, n is a convenient number
if and only if for every x ≥ 0 such that q = n + x 2 ≤ 4n/3 , if q = rs
and 2x ≤ r ≤ s, then r = s or r = 2x.
For example, 60 is a convenient number, because
60 + 1 2 = 61 (�),
60 + 2 2 = 64 = 4 · 16 = 8 · 8,
60 + 3 2 = 69 (�),
60 + 4 2 = 76 (�)
and the numbers marked with a (�) do not have a factorization of
the form indicated.
Euler showed, for example, that 1848 is a convenient number,
and that
q = 18518809 = 197 2 + 1848 · 100 2
is a prime number. At Euler’s time, this was quite a feat.
Gauss understood convenient numbers in terms of his theory of
binary quadratic forms. The number n is convenient if and only if
each genus of the form x 2 + ny 2 has only one class.
Here is a list of the 65 convenient numbers found by Euler:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 13, 15, 16, 18, 21, 22, 24, 25,
28, 30, 33, 37, 40, 42, 45, 48, 57, 58, 60, 70, 72, 78, 85, 88, 93,
102, 105, 112, 120, 130, 133, 165, 168, 177, 190, 210, 232, 240,
253, 273, 280, 312, 330, 345, 357, 385, 408, 462, 520, 760, 840,
1320, 1365, 1848.
Are there other convenient numbers? Chowla showed that there
are only finitely many convenient numbers; later, finer analytical
work (for example, by Briggs, Grosswald, and Weinberger)
implied that there are at most 66 convenient numbers.
The problem is difficult. The exclusion of an additional numerus
idoneus is of a kind similar to the exclusion of a hypothetical tenth358
imaginary quadratic field (by Heegner, Stark, and Baker), which
I have already mentioned.
My numbers, my friends /Paulo Ribenboim
Δείτε επίσης εδώ για numeris idonei