Κατ’ αρχάς θα δεχτούμε ότι το κλάσμα ![]() παριστάνει το πηλίκο της διαίρεσης
παριστάνει το πηλίκο της διαίρεσης ![]() . Έτσι λοιπόν έχουμε ότι
. Έτσι λοιπόν έχουμε ότι ![]() . Μέσα από αυτό τον ορισμό προκύπτουν εύκολα οι παρακάτω ιδιότητες των κλασμάτων:
. Μέσα από αυτό τον ορισμό προκύπτουν εύκολα οι παρακάτω ιδιότητες των κλασμάτων:
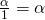 αφού
αφού 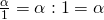
Σύμφωνα με αυτή την ιδιότητα κάθε αριθμός μπορεί να γραφεί σαν κλάσμα, αρκεί να του βάλουμε παρονομαστή το 1.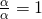 αφού
αφού 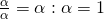
Εδώ βλέπουμε ότι όταν σε ένα κλάσμα ο αριθμητής και ο παρονομαστής είναι ίσοι, τότε το κλάσμα είναι ίσο με 1. Και αντίστροφα αν δούμε ότι συμβαίνει αυτό: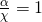 ή αυτό:
ή αυτό: 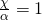 τότε αμέσως συμπεραίνουμε ότι:
τότε αμέσως συμπεραίνουμε ότι: 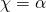 Δηλαδή ισχύει:
Δηλαδή ισχύει:  και
και  και λίγο πιο συνοπτικά:
και λίγο πιο συνοπτικά: 
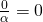 αφού
αφού 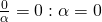
Από αυτή την ιδιότητα έχουμε ότι ένα κλάσμα είναι ίσο με το 0 αν και μόνο αν ο αριθμητής του είναι το 0. Δηλαδή ισχύει: Παρατήρηση: Ο παρονομαστής του κλάσματος δεν μπορεί να είναι μηδέν αφού όπως είδαμε και στην Ευκλείδεια Διαίρεση δεν επιτρέπεται διαίρεση με το 0.
Παρατήρηση: Ο παρονομαστής του κλάσματος δεν μπορεί να είναι μηδέν αφού όπως είδαμε και στην Ευκλείδεια Διαίρεση δεν επιτρέπεται διαίρεση με το 0.
Συγκεντρωτικά:
| Ιδιότητες Κλασμάτων |
|
|
|
|
|
|
|
|
![]()
![]()

