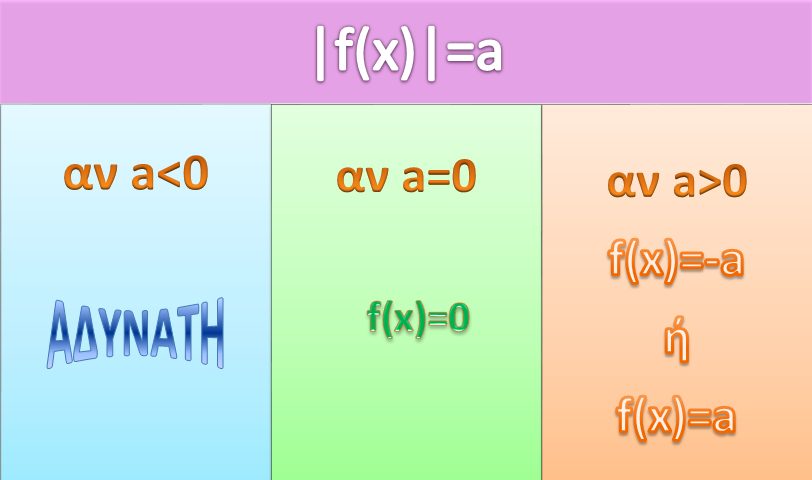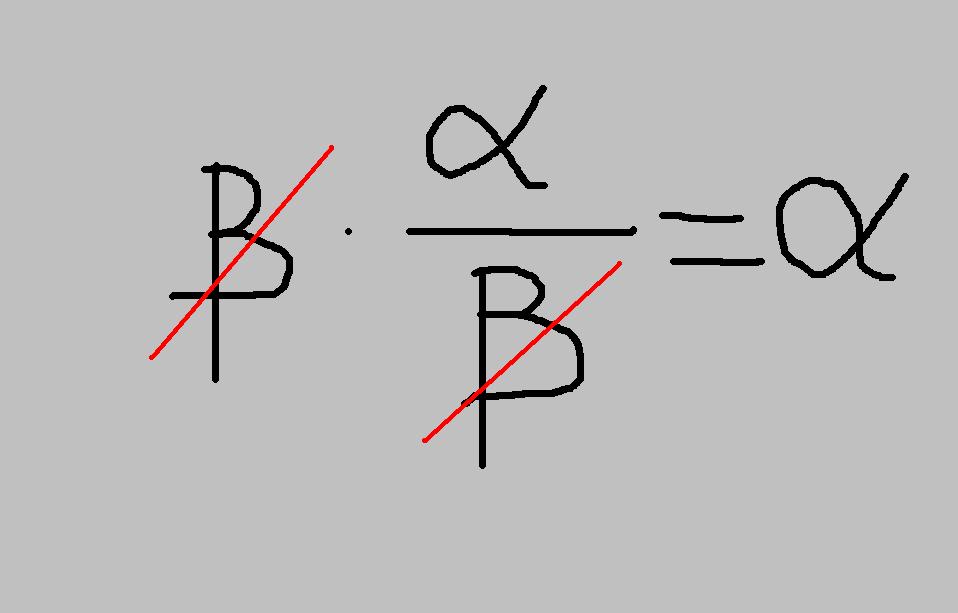Εξίσωση – mathland

Επίλυση δευτεροβάθμιας εξίσωσης

Αφού είδαμε θεωρητικά το πως μπορούμε να βρούμε τις λύσεις μιας δευτεροβάθμιας εξίσωσης, καλό θα ήταν να το εφαρμόσουμε και στην πράξη

Continue reading «Επίλυση δευτεροβάθμιας εξίσωσης»

Εξισώσεις 2+ βαθμού

Στην Β΄ Γυμνασίου μάθαμε έναν αλγόριθμο (μεθοδολογία) για να επιλύουμε κάθε εξίσωση πρώτου βαθμού.
Τώρα στη Τρίτη τάξη θα δούμε πως μπορούμε κάτω από ορισμένες συνθήκες να βρούμε τις λύσεις και σε άλλες εξισώσεις μεγαλύτερου βαθμού. Η μέθοδος αυτή δεν αποδίδει πάντα, γι’ αυτό αργότερα θα την συμπληρώσουμε

πως μας βοηθά η παραγοντοποίηση στην επίλυση εξισώσεων δεύτερου βαθμού ή μεγαλύτερου.

Πριν όμως από αυτό θα πρέπει να δούμε μια σημαντική ιδιότητα:

$A \cdot\ B=0\Leftrightarrow \left \{ \begin{matrix} A=0\\ \eta\\ B=0 \end{matrix} \right.$

Η οποία μας λέει ότι ένα γινόμενο είναι ίσο με μηδέν τότε και μόνο τότε αν τουλάχιστον ένας από τους παράγοντες του γινομένου είναι ίσος με μηδέν.

Να δούμε τώρα λύνοντας ένα παράδειγμα πως μπορούμε να εκμεταλλευτούμε τα παραπάνω για να βρούμε τις λύσεις σε μια εξίσωση 2ου βαθμού. Έστω λοιπόν ότι ψάχνουμε να βρούμε εκείνους τους αριθμούς που ικανοποιούν τη σχέση $x^2-x=0$ . Αυτή είναι μια δευτεροβάθμια εξίσωση την οποία και θα μετατρέψω σε γινόμενο (με κάποια από τις μεθόδους παραγοντοποίησης που μάθαμε) με σκοπό να χρησιμοποιήσω την ιδιότητα που προαναφέραμε. Έτσι έχουμε

$x^2-x=0\Leftrightarrow$

(βγάζουμε κοινό παράγοντα το x)

$x\cdot(x-1)=0$

φτάσαμε λοιπόν στο σημείο να έχουμε ένα γινόμενο που είναι ίσο με το μηδέν. Το γινόμενο αυτό αποτελείται από δύο (πρωτοβάθμιους) παράγοντες τον x και τον x-1. Σύμφωνα με την ιδιότητα που αναφέραμε παραπάνω συμπεραίνουμε ότι τουλάχιστον ένας από αυτούς τους παράγοντες θα είναι ίσος με μηδέν. Δηλαδή θα ισχύει:

$\left \{ \begin{matrix} x=0\\ \eta\\ x-1=0\Leftrightarrow x=1 \end{matrix} \right.$

Από τον τρόπο που λύθηκε το προηγούμενο παράδειγμα φαίνεται το ποια μέθοδο πρέπει ν’ ακολουθούμε για να επιλύσουμε μια εξίσωση που έχει βαθμό μεγαλύτερο του πρώτου:

[su_label style=»important»]Βήμα 1ο:[/su_label] Μεταφέρουμε όλους τους όρους στο α’ μέλος έτσι ώστε στο δεύτερο μέλος να είναι ίσο με μηδέν.

[su_label style=»success»]Βήμα 2ο:[/su_label] Μετατρέπουμε σε γινόμενο το α’ μέλος.

[su_label style=»warning»]Βήμα 3ο:[/su_label] Παίρνουμε κάθε παράγοντα του γινομένου ίσο με μηδέν.

[su_label style=»info»]Βήμα 4ο:[/su_label] Λύνουμε κάθε μια από τις εξισώσεις (1ου βαθμού) που προκύπτουν από το προηγούμενο βήμα.

Θέλω να μάθω … να λύνω εξισώσεις με απόλυτα

Για να λύσουμε εξισώσεις με απόλυτες τιμές (που ο άγνωστος είναι «φυλακισμένος» μέσα σε απόλυτα) πρέπει να ελευθερώσουμε τον άγνωστο από το απόλυτο. Πως μπορούμε να το πετύχουμε;

ΑΛΓΕΒΡΑ Α΄ ΛΥΚΕΙΟΥ

Για το πως μπορούμε να απαλλαγούμε από τις απόλυτες τιμές που τυχόν εμφανίζονται σε μία αλγεβρική παράσταση έχουμε αναφερθεί σε προηγούμενο άρθρο μας (και καλό θα ήταν να του ρίξετε μια ματιά κάνοντας κλικ εδώ). Σε αυτή τη δημοσίευση θα ασχοληθούμε με εξισώσεις στις οποίες ο άγνωστος βρίσκεται πίσω από τις μπάρες της απόλυτης τιμής. Εξισώσεις δηλαδή που ο άγνωστος είναι «φυλακισμένος» μέσα σε μία ή και περισσότερες απόλυτες τιμές. Σκοπός μας σε μια τέτοια εξίσωση (όπως και σε κάθε εξίσωση άλλωστε) είναι να βρούμε ποιος αριθμός είναι «κρυμμένος πίσω από τη μάσκα του x». Στόχος μας είναι να «ελευθερώσουμε» το x μέσα από την απόλυτη τιμή. Για να το καταφέρουμε αυτό ας θυμηθούμε πρώτα τι είναι η απόλυτη τιμή ενός αριθμού και μετά βλέπουμε πως λύνουμε την εξίσωση.

Η απόλυτη τιμή ενός αριθμού ορίζεται και αλγεβρικά και γεωμετρικά. Εμείς θα αρκεστούμε στο δεύτερο μιας και είναι αρκετό για να στηριχτούμε σε αυτό και να καταφέρουμε να λύσουμε τις εξισώσεις.

Τι είναι λοιπόν η απόλυτη τιμή;

Γνωρίζουμε ότι κάθε πραγματικός αριθμός x παριστάνεται με ένα σημείο πάνω στον άξονα των πραγματικών αριθμών. Την απόσταση του σημείου αυτού από το 0 τη λέμε απόλυτη τιμή του αριθμού x και τη συμβολίζουμε |x|.

absolute — Η απόλυτη τιμή ενός αριθμού εκφράζει την απόστασή του από το 0, χωρίς να μας ενδιαφέρει η σχετική του θέση αν δηλαδή βρίσκεται πριν ή μετά το 0

Έτσι μπορούμε να εξηγήσουμε και πολλές από τις ιδιότητες της απόλυτης τιμής όπως

Η απόλυτη τιμή οποιουδήποτε αριθμού είναι είτε θετικός αριθμός είτε μηδέν, γιατί όπως είναι γνωστό αρνητική απόσταση δεν υπάρχει. Έτσι έχουμε,
$|x|\geq0$

Οι αντίθετοι αριθμοί έχουν την ίδια απόλυτη τιμή, αφού ισαπέχουν από το 0.
$|-x|=|x|$

Ας δούμε τώρα τι γίνεται με τις εξισώσεις.

Σας θυμίζω ότι για να αντιλαμβανόμαστε καλύτερα τις εξισώσεις μπορούμε να τις θεωρούμε σαν ερωτήσεις. Έτσι η εξίσωση |x|= -5 , μας ρωτάει ποιος αριθμός είναι αυτός που απέχει από το 0 -5 μονάδες; Προφανώς η απάντηση είναι κανένας (αναφέραμε και πιο πάνω ότι δεν νοείται αρνητική απόσταση). Ενώ η απάντηση στην ερώτηση(=εξίσωση) |x|=0 είναι «ο μοναδικός αριθμός που απέχει από το μηδέν 0 μονάδες είναι ο 0». Όμως η εξίσωση |χ|=2 μας ζητάει να βρούμε τον αριθμό που απέχει από το 0 2 μονάδες. Η απάντηση είναι ότι δεν υπάρχει μόνο ένας αριθμός με αυτή την ιδιότητα αλλά δύο αριθμοί ο 2 και ο -2. Έτσι η εξίσωσή μας έχει δύο λύσεις τις x=2 ή x= -2. Για να γενικεύσουμε λίγο τα πράγματα και να τα βάλουμε σε μία τάξη δείτε το παρακάτω σχεδιάγραμμα.

Εξισώσεις με απόλυτα — Προσοχή! Όταν a>0 έχουμε 2 λύσεις

Όπου βλέπετε f(x) θα εννοούμε «μια παράσταση που περιέχει x». Γιατί μέσα στο απόλυτο δεν είναι απαραίτητο να υπάρχει μόνο x, μπορεί κάποιοι «κακοί μαθηματικοί» (σαν κι εμένα) να ζητήσουν να λυθούν εξισώσεις που μέσα στο απόλυτο να υπάρχουν αρκετά πράγματα.

Για να λύσουμε οποιαδήποτε εξίσωση στην οποία το x βρίσκεται μέσα σε απόλυτο, πρέπει να στηριχτούμε στα συμπεράσματα του παραπάνω πίνακα. Πρέπει λοιπόν να απομονώσουμε το απόλυτο στο ένα μέλος και μετά κοιτώντας τι ρόλο παίζει το άλλο μέλος να αποφανθούμε αν η εξίσωση έχει λύσεις ή όχι και στην περίπτωση που έχει ποιες είναι αυτές. Ας δούμε τώρα μερικά παραδείγματα:

Άσκηση 1: Να λυθεί η εξίσωση $\frac{4-5|x|}{12}-\frac{3|x|-3}{2}=2|-x|-6$

[gn_spoiler title=»Λύση:»]Φαίνεται η εξίσωση μας να έχει δύο διαφορετικές απόλυτες τιμές την |x| και την |-x|. Αυτό όμως δεν αληθεύει γιατί ξέρουμε ότι |-x|=|x|. Οπότε μπορούμε στην εξίσωση που μας δώσανε όπου έχει |-x| εμείς να βάλουμε |x|. Για να απομονώσουμε το απόλυτο που θέλουμε θα ακολουθήσουμε τη γνωστή διαδικασία που ακολουθούμε σε όλες τις εξισώσεις α΄ βαθμού.
Πρώτα θα διώξουμε τους παρονομαστές πολλαπλασιάζοντας κάθε όρο με το Ε.Κ.Π. των παρονομαστών που είναι το 12

$12\frac{4-5|x|}{12}-12\frac{3|x|-3}{2}=12\cdot 2|x|-12\cdot 6 \Leftrightarrow$

$4-5|x|-6(3|x|-3)=24|x|-72$

Τώρα διώχνουμε τις παρενθέσεις κάνοντας χρήση της επιμεριστικής ιδιότητας

$4-5|x|-18|x|+18=24|x|-72$

Χωρίζουμε τους γνωστούς από τους άγνωστους ώστε να μπορέσουμε να συνεχίσουμε τις πράξεις χωρίς να ξεχνάμε ότι προς το παρόν άγνωστος είναι το |x| κι όχι το x

$-5|x|-18|x|-24|x|=-4-18-72\Leftrightarrow$

$-47|x|=-94\Leftrightarrow 47|x|=94$

άρα

$|x|=\frac{94}{47}$

ή πιο απλά

$|x|=2$

Αφού καταφέραμε κι απομονώσαμε το απόλυτο μπορούμε σύμφωνα με όσα έχουμε πει πιο πάνω ν΄απαντήσουμε ότι $x=2$ ή $x=-2$
[/gn_spoiler]

Άσκηση 2: Να λυθεί η εξίσωση $\frac{4-5|x-1|}{12}-\frac{3|x-1|-3}{2}=2|1-x|-6$

[gn_spoiler title=»Λύση:»]Όπως θα παρατηρήσατε η εξίσωση αυτή είναι ίδια με την προηγούμενη με την μόνη αλλαγή αντί για |x| έχουμε |x-1|. Και πάλι επειδή οι αριθμοί 1-x και x-1 είναι αντίθετοι η εξίσωση θα γίνει

$\frac{4-5|x-1|}{12}-\frac{3|x-1|-3}{2}=2|x-1|-6$

και θα λυθεί με τον ίδιο ακριβώς τρόπο καταλήγοντας στο

$|x-1|=2 \Leftrightarrow\left\{\begin{matrix}x-1=-2\Leftrightarrow x=-2+1=-1\\ \eta\\x-1=2\Leftrightarrow x=2+1=3\end{matrix}$

Έτσι λοιπόν βλέπουμε ότι αν τα απόλυτα που έχουμε στην εξίσωση περιέχουν ίσες ή ακόμη και αντίθετες παραστάσεις, τότε δεν μας ενδιαφέρει το περιεχόμενη της απόλυτης τιμής. Λύνουμε την εξίσωση κανονικά όπως όλες τις εξισώσεις «κουβαλώντας» το απόλυτο μέχρι να καταφέρουμε να το απομονώσουμε και στο τέλος το πετάμε (πάντα σύμφωνα με το διάγραμμα που έχουμε παραπάνω).
Επειδή κάποιοι μπορεί να «ψιλό» μπερδεύονται κουβαλώντας το απόλυτο μπορούν να γλυτώσουν από αυτό με την συνηθισμένη στα μαθηματικά μέθοδο: «αν κάτι μ΄ενοχλεί κάνω πως δεν το βλέπω». Έτσι λοιπόν θα μπορούσαμε να θέσουμε όπου |x-1|=α (σχέση 1) και να λύσουμε την εξίσωση χωρίς το απόλυτο. Μόλις ξεμπερδέψουμε με το α και το βρούμε γυρίζουμε και το αντικαθιστούμε στη σχέση 1 απ’ όπου υπολογίζουμε το x που μας ενδιαφέρει.
Watch me
Θέτω |χ-1|=α (σχέση 1) οπότε η εξίσωση γίνεται

$\frac{4-5a}{12}-\frac{3a-3}{2}=2a-6\Leftrightarrow$

$12\frac{4-5a}{12}-12\frac{3a-3}{2}=12\cdot 2a-12\cdot 6 \Leftrightarrow$

$4-5a-6(3a-3)=24a-72\Leftrightarrow$

$-5a-18a-24a=-4-18-72\Leftrightarrow$

$-47a=-94\Leftrightarrow a=2$

Ας μην ξεχνάμε όμως ότι δεν ψάχναμε το α αλλά το x. Πάμε λοιπόν στη σχέση 1 και αντικαθιστούμε όπου α=2, οπότε

$|x-1|=a \Leftrightarrow|x-1|=2 \Leftrightarrow\left\{\begin{matrix}x-1=-2\Leftrightarrow x=-2+1=-1\\ \eta\\x-1=2\Leftrightarrow x=2+1=3 \end{matrix}$

Τη μέθοδο αυτή για να είμαι ειλικρινής δεν σας την έδειξα μόνο για την περίπτωση που κάποιος δυσκολεύεται με τα πολλά απόλυτα αλλά και γιατί σε κάποιες περιπτώσεις θα έλεγα δεν μπορούμε να την αποφύγουμε γι’ αυτό καλό είναι να την ξέρουμε. Δείτε την επόμενη άσκηση και θα καταλάβετε. [/gn_spoiler]

Άσκηση 3: Να βρεθούν οι αριθμοί που ικανοποιούν τη σχέση $2-|x|=x^2$

[gn_spoiler title=»Λύση:»] Την άσκηση αυτή θα μπορούσαμε να τη λύσουμε απομονώνοντας το απόλυτο στο ένα μέλος, οπότε η εξίσωση να γίνει |x|=2 – x² αλλά πιστεύω ότι έτσι δεν θα μας συνέφερε γιατί το δεύτερο μέλος (το 2 – x²) δεν γνωρίζουμε αν είναι θετικός ή αρνητικός αριθμός ( για κάποιες τιμές του x γίνεται θετικός, για κάποιες αρνητικός και για κάποιες γίνεται ίσος με 0). Έτσι θα έπρεπε να διακρίνουμε περιπτώσεις και να πούμε

Περίπτωση 1η: αν το 2 – x² είναι αρνητικό η εξίσωσή μας είναι αδύνατη (βλέπε και το σχεδιάγραμμα πιο πάνω)

Περίπτωση 2η: αν $2 - x^2\geq0$ , τότε x=2-x² ή x= – (2-x²) και να λύσω δύο εξισώσεις (δεύτερου βαθμού η καθεμία) κι αφού βρω τις λύσεις να κρατήσω από αυτές μόνο εκείνες που επαληθεύουν τον περιορισμό $2 - x^2\geq0$ .

Για να γλυτώσουμε όλη αυτή τη δουλειά μπορούμε να σκεφτούμε λίγο πιο έξυπνα και να αντικαταστήσουμε το |x| με έναν άλλο αριθμό έστω α. Τότε θα έχουμε γλυτώσει και από το |x| αλλά και από το x² γιατί το x²=|x²|=|x|²=α² (ρίξε μια ματιά στις ιδιότητες των απολύτων). Ας δούμε τώρα πως έχει καταντήσει η εξίσωσή μας θέτοντας |x|=α,

$2-a=a^2\Leftrightarrow a^2+a-2=0$

Η διακρίνουσα του τριωνύμου είναι

$\Delta=1^2-4(-2)=9$

και οι λύσεις της εξίσωσης αυτής είναι

$a=1$

$a=-2$

Εύκολα λοιπόν βρήκαμε το α, το x όμως είναι αυτό που μας ενδιαφέρει

$\left | x \right |=\alpha \Leftrightarrow \left\{\begin{matrix} \left | x \right |=1 \Leftrightarrow x=\pm 1\\\eta'\\ \left | x \right |=-2 & \alpha \delta \upsilon \nu \alpha \tau \eta \end{matrix}\right.$

[/gn_spoiler]

Άσκηση 4: Να βρεθούν οι αριθμοί που ικανοποιούν τη σχέση $|2x+3|=|x+9|$

[gn_spoiler title=»Λύση:»] Στην άσκηση αυτή ανήκει στη γενική κατηγορία

$|f(x)|=|g(x)|$

και λύνεται με την ισοδυναμία

$|f(x)|=|g(x)| \Leftrightarrow \left\{\begin{matrix}f(x)=g(x)\\ \eta\\f(x)=-g(x) \end{matrix}$

Έχουμε λοιπόν $|2x+3|=|x+9| \Leftrightarrow \left\{\begin{matrix}2x+3=x+9\\ \eta\\2x+3=-x-9 \end{matrix}\Leftrightarrow$

$\left\{\begin{matrix}2x-x=-3+9\Leftrightarrow x=6\\ \eta\\2x+x=-3-9\Leftrightarrow x=-4 \end{matrix}$ [/gn_spoiler]

Θέλω να μάθω … να λύνω κλασματικές εξισώσεις

Ας δούμε ποια εξίσωση λέγεται κλασματική, πως βρίσκουμε τις λύσεις της και πως τους περιορισμούς. Δείτε πόσο σημαντικό είναι να μην ξεχνάμε να παίρνουμε περιορισμούς κάθε φορά που μια μεταβλητή εμφανίζεται σε παρονομαστή.

Κατ’ αρχάς ας δούμε τι εννοούμε όταν λέμε «κλασματικές εξισώσεις». Πολλοί μπορεί να θεωρούν ότι μια εξίσωση που έχει κλάσματα είναι μια κλασματική εξίσωση. Αυτό όμως δεν είναι σωστό γιατί μια εξίσωση τη λέμε κλασματική μόνο στη περίπτωση που υπάρχει άγνωστος σε ένα τουλάχιστον παρονομαστή της. Έτσι λοιπόν η εξίσωση $\frac{x^2-1}3-\frac{x+3}5=x-2$ ναι μεν έχει κλάσματα αλλά δεν είναι κλασματική αφού δεν υπάρχει άγνωστος σε κανένα παρονομαστή, ενώ η εξίσωση $\frac{6}{x^2+3x}+\frac{x+2}{x}=\frac{x+1}{x+3}$ σύμφωνα με αυτά που προαναφέραμε είναι μια κλασματική εξίσωση αφού ο άγνωστος x «κυκλοφορεί» σε παρονομαστές. Δηλαδή ο x «δουλεύει υπογείως (ύπουλα)» πράγμα επικίνδυνο όπως θα δούμε παρακάτω.

Στη συνέχεια θα επιλύσουμε μια κλασματική εξίσωση για να δούμε ποια μέθοδο ακολουθούμε και τι πρέπει να προσέξουμε.

Να βρείτε τις λύσεις της παρακάτω εξίσωσης $\frac{6}{x^2+3x}+\frac{x+2}{x}=\frac{x+1}{x+3}$

[wptabs mode=»horizontal»] [wptabtitle] Επίλυση[/wptabtitle] [wptabcontent]


$\frac{6}{x^2+3x}+\frac{x+2}{x}=\frac{x+1}{x+3}$ Όπως σε όλες τις κατηγορίες εξισώσεων το πρώτο πράγμα που πρέπει να κάνουμε είναι να απαλλαγούμε από τους παρονομαστές (αν υπάρχουν)
$\frac{6}{x(x+3)}+\frac{x+2}{x}=\frac{x+1}{x+3}$ Για να το πετύχουμε αυτό πρέπει να παραγοντοποιήσουμε όσους από τους παρονομαστές παραγοντοποιούνται. Στην άσκησή μας ο μόνος που μπορεί να παραγοντοποιηθεί είναι ο $x^2+3x=x(x+3)$ (βγάλαμε κοινό παράγοντα το x). Στη συνέχεια αντικαθιστούμε τους παρονομαστές με τους νέους τους παραγοντοποιημένους.
$x(x+3)\frac{6}{x(x+3)}+x(x+3)\frac{x+2}{x}=x(x+3)\frac{x+1}{x+3}$ Τώρα είμαστε σε θέση να βρούμε το Ε.Κ.Π., που είναι το γινόμενο όλων των παρονομαστών με την προϋπόθεση όμως κάθε παράγοντας να εμφανίζεται μία μόνο φορά και μάλιστα στη μεγαλύτερη δύναμη. Στο παράδειγμά μας το Ε.Κ.Π.=χ(χ+3). Πολλαπλασιάζουμε τώρα όλους τους όρους της εξίσωσης με το Ε.Κ.Π.
$6+(x+3)(x+2)=x(x+1)$ Μετά από τις απλοποιήσεις έχουμε μια εξίσωση χωρίς παρονομαστές, όπως φαίνεται δίπλα. Σειρά τώρα για «αποχώρηση» έχουν οι παρενθέσεις ώστε να απελευθερώσουμε το x. Αυτό γίνεται με τη βοήθεια της επιμεριστικής ιδιότητας
$6+x^2+2x+3x+6=x^2+x$ $6+x^2+5x+6=x^2+x$ $12+4x=0$ $4x=-12$ $x=-\frac{12}4$ Συμμαζεύοντας λίγο (κάνουμε αναγωγή όμοιων όρων) θα προκύψει μια εξίσωση 1ου (οπότε χωρίζουμε γνωστούς – άγνωστους κτλ) ή 2ου βαθμού (τα μεταφέρουμε όλα στο ένα μέλος, υπολογίζουμε τη διακρίνουσα κτλ). Στην άσκηση που προσπαθούμε να λύσουμε τώρα παρότι δείχνει δεύτερου βαθμού (αφού έχει x²) αν τη δουλέψουμε λίγο θα δούμε ότι μετά την αναγωγή των όμοιων όρων θα προκύψει μια εξίσωση πρώτου βαθμού οπότε
$x=-3$ βρίσκουμε τελικά πως η εξίσωση που μας δόθηκε έχει λύση τον αριθμό -3.

Μετά από αρκετό κόπο θα έλεγα φτάσαμε στο να βρούμε ότι η εξίσωση $\frac{6}{x^2+3x}+\frac{x+2}{x}=\frac{x+1}{x+3}$ έχει λύση το x=-3.

Κι όμως έχουμε κάνει ΜΕΓΑΛΟ ΛΑΘΟΣ κι αν έχεις κάνει το κόπο να φτάσεις μέχρι εδώ καλό θα ήταν να κάνεις κλικ στην καρτέλα «Περιορισμοί» για να δεις ποιο είναι το λάθος που κάναμε και πόσο σοβαρό είναι.

Επιστροφή^^^
[/wptabcontent]

[wptabtitle]Περιορισμοί[/wptabtitle] [wptabcontent]Όταν έχουμε να λύσουμε μια εξίσωση αναζητούμε ποια τιμή (ή ποιες τιμές) μπορεί να πάρει η άγνωστη μεταβλητή έτσι ώστε αν την αντικαταστήσουμε στην εξίσωση να προκύψει μια αληθής ισότητα (για παράδειγμα η λύση της εξίσωσης 2χ-8=0 είναι ο αριθμός 4 γιατί αν αντικαταστήσουμε το χ με τον αριθμό 4 θα προκύψει 2^.4-8=0 που είναι μια σωστή πρόταση.

Στο προηγούμενο όμως άρθρο είχαμε αναφερθεί στους περιορισμούς (κάντε κλικ εδώ για να το δείτε). Εκεί λοιπόν είπαμε ότι δεν έχει νόημα στα μαθηματικά κλάσμα με παρονομαστή το 0. Γιαυτό όταν λύνουμε κλασματικές εξισώσεις θα πρέπει εκ των προτέρων να θέτουμε περιορισμούς για τον άγνωστο. Δηλαδή από την αρχή να δηλώνουμε ότι για τον άγνωστο, έστω χ, δεν μπορούμε να δεχτούμε κάποιες τιμές γιατί μηδενίζουν κάποιον από τους παρονομαστές της εξίσωσης.

Κατά την επίλυση μιας εξίσωσης σε όποια κατηγορία κι αν ανήκει αυτή (1ου ή 2ου βαθμού ή και κλασματική) σε κάθε μας βήμα (όταν διώχνουμε παρονομαστές, παρενθέσεις κτλ) δημιουργούμε μια άλλη εξίσωση πιο απλή από την αρχική που έχει ως λύσεις της τις λύσεις της προηγούμενης αλλά πιθανόν να έχει κι άλλες (περισσότερες). Στο τέλος τις επιπλέον λύσεις θα πρέπει να τις απορρίψουμε, να μην τις δεχτούμε δηλαδή ως λύσεις της αρχικής εξίσωσης. Αυτό ακριβώς έχει συμβεί και με την εξίσωση $\frac{6}{x^2+3x}+\frac{x+2}{x}=\frac{x+1}{x+3}$ γιατί στην πορεία πήρε διάφορες μορφές μέχρι που κατέληξε να γίνει 4χ=-12. Εμείς βρήκαμε ότι χ=-3 αυτή όμως η λύση είναι η λύση της 4χ=-12 (γιατί αν βάλουμε όπου χ το -3 προκύπτει μια αληθής πρόταση η 4^.(-3)=-12 και όχι της $\frac{6}{x^2+3x}+\frac{x+2}{x}=\frac{x+1}{x+3}$ γιατί εδώ δεν μπορούμε καν να βάλουμε όπου χ το -3 αφού θα μας μηδενίσει κάποιους παρονομαστές (τον χ²+3χ και τον χ+3).

Τι πρέπει να κάνουμε λοιπόν σε τέτοιες περιπτώσεις;

Πρέπει να παίρνουμε τα μέτρα μας, δηλαδή να παίρνουμε περιορισμούς.

ΚΑΘΕ ΠΑΡΟΝΟΜΑΣΤΗΣ ΠΡΕΠΕΙ ΝΑ ΜΗΝ ΓΙΝΕΤΑΙ ΙΣΟΣ ΜΕ 0

κι επειδή μέσα στο Ε.Κ.Π. είναι «κρυμμένοι» όλοι οι παρονομαστές της εξίσωσης είναι αρκετό να απαιτούμε

ΤΟ Ε.Κ.Π. ΝΑ ΜΗΝ ΓΙΝΕΤΑΙ ΠΟΤΕ ΙΣΟ ΜΕ 0 ( $E.K.\Pi.\neq 0$ ).

Στη συγκεκριμένη επομένως άσκηση θα έπρεπε την ώρα που βρήκαμε το Ε.Κ.Π. να γράφαμε: $E.K.\Pi.=x(x+3)\neq 0$ πράγμα που σημαίνει ότι και το x αλλά και το x+3 πρέπει να είναι διάφορα του 0 δηλαδή με άλλα λόγια δεν μπορούμε να δεχτούμε σαν λύσεις ούτε το 0 αλλά ούτε και το -3. Πιο σύντομα και πιο «μαθηματικά» όλα τα παραπάνω θα μπορούσαν να γραφούν ως εξής:

$E.K. /Pi=x(x+3)\neq 0 \Leftrightarrow$

$x\neq 0 \kappa\alpha\iota x+3\neq 0\Leftrightarrow$

$x\neq 0 \kappa\alpha\iota x\neq -3$

Βλέπουμε λοιπόν ότι η εξίσωση που λύναμε τελικά δεν έχει λύση το -3 , άρα δεν έχει καμία λύση ήταν δηλαδή αδύνατη. Ξεχνώντας όμως τους περιορισμούς «την πατήσαμε». Επιστροφή^^^
[/wptabcontent]

[wptabtitle]Σε Έκτακτη Περίπτωση[/wptabtitle] [wptabcontent]Αν σε κάποια περίπτωση αδυνατούμε να βρούμε τους περιορισμούς είτε γιατί κάποιος δυσκολεύεται είτε γιατί δεν προλαβαίνει (π.χ. σε διαγώνισμα) τότε μπορεί να αποφύγει τα παραπάνω και απλώς να ελέγξει αν οι λύσεις που βρήκε μηδενίζουν το Ε.Κ.Π. και
αν το Ε.Κ.Π. μηδενίζεται, τότε η λύση απορρίπτεται αν όχι γίνεται δεκτή.
Στην άσκησή μας το Ε.Κ.Π. = $x(x+3)$ για x=-3 γίνεται Ε.Κ.Π.=-3^.(-3+3)=-3^.0=0 κι επομένως η λύση x=-3 απορρίπτεται.

Μπορεί να σας κούρασα με την μεγάλη έκταση που είχε το άρθρο αλλά θεωρώ τις κλασματικές εξισώσεις λιγάκι δύσκολες για μαθητές Γ΄ Γυμνασίου αλλά και πολύ σημαντικές για τη συνέχεια. Αυτό που πρέπει να θυμόμαστε τελικά είναι πως οι κλασματικές εξισώσεις λύνονται όπως και όλες οι υπόλοιπες δηλαδή:

διώχνουμε παρονομαστές (πολλαπλασιάζοντας με το Ε.Κ.Π.)
διώχνουμε παρενθέσεις (με επιμεριστική)
συμμαζεύουμε λίγο (αναγωγή όμοιων όρων)

έτσι προκύπτει μια εξίσωση 1ου ή 2ου βαθμού που λύνουμε ανάλογα και

τέλος

ΔΕΝ ΞΕΧΝΑΜΕ ΝΑ ΕΛΕΓΞΟΥΜΕ ΑΝ ΟΙ ΛΥΣΕΙΣ ΠΟΥ ΒΡΗΚΑΜΕ ΠΕΡΝΟΥΝ ΤΟ (CRASH) TEST ΤΩΝ ΠΕΡΙΟΡΙΣΜΩΝ (δηλαδή να μην μηδενίζουν το Ε.Κ.Π.).

[/wptabcontent][/wptabs]

Θέλω να μάθω να λύνω … τριγωνομετρικές εξισώσεις

Τριγωνομετρική εξίσωση λέγεται η εξίσωση στην οποία ο άγνωστος είναι «φυλακισμένος» μέσα σε κάποιο τριγωνομετρικό αριθμό. Οι τριγωνομετρικές εξισώσεις (λόγω της περιοδικότητας που παρουσιάζουν οι τριγωνομετρικές συναρτήσεις) έχουν άπειρες λύσεις που χωρίζονται σε δύο ομάδες. Για να μπορέσουμε να λύσουμε τριγωνομετρικές εξισώσεις θα πρέπει να ελευθερώσουμε τον άγνωστο μέσα από τον τριγωνομετρικό αριθμό, για να το πετύχουμε αυτό ακολουθούμε τα παρακάτω βήματα:

Βήμα 1⁰

Απομονώνουμε τον τριγωνομετρικό αριθμό που περιέχει τον άγνωστο στο ένα μέλος.

Βήμα 2⁰

Βρίσκουμε μια «αρχική λύση» για την εξίσωσή μας, δηλαδή μια γωνία από 0^οεως 360^ο που να ικανοποιεί την εξίσωση.

Βήμα 3⁰

Χρησιμοποιούμε τους παρακάτω τύπους λύσεων, ανάλογα με την περίπτωση:

Τύποι λύσεων για τριγωνομετρικές εξισώσεις

Εξίσωση	Λύσεις ( ${k\in\mathbb{Z}}$ )
$\eta\mu X=\eta\mu\Theta$	$X=2k\pi+\Theta$ ή $X=2k\pi+(\pi-\Theta)$
$\sigma\upsilon\nu X=\sigma\upsilon\nu\Theta$	$X=2k\pi\pm\Theta$
$\epsilon\phi X=\epsilon\phi\Theta$	$X=k\pi+\Theta$
$\sigma\phi X=\sigma\phi\Theta$	$X=k\pi+\Theta$

Ας δούμε κι ένα παράδειγμα για να καταλάβουμε καλύτερα τη διαδικασία επίλυσης μιας τριγωνομετρικής εξίσωσης:

Άσκηση: Να λυθεί η εξίσωση $2\sigma\upsilon\nu x-1=0$

Λύση:

Βήμα 1⁰: απομονώνουμε το συνημίτονο (το θεωρούμε ως άγνωστο, χωρίζουμε γνωστούς από άγνωστους και διαιρούμε με το συντελεστή του άγνωστου)

$2\sigma\upsilon\nu x-1=0\Leftrightarrow$

$2\sigma\upsilon\nu x=1\Leftrightarrow$

$\sigma\upsilon\nu x=1/2$

Βήμα 2⁰: Βρίσκουμε μια γωνία στο διάστημα [0 – 2π] που να ικανοποιεί την εξίσωση αυτή.

Η γωνία π/3 έχει συνημίτονο ίσο με 1/2, δηλαδή

$\sigma\upsilon\nu(\pi/3)=1/2$ και $\sigma\upsilon\nu x=1/2$

άρα ισχύει

$\sigma\upsilon\nu x=\sigma\upsilon\nu(\pi/3)$

Βήμα 3^ο: Από τους τύπους των λύσεων παίρνω,

$x=2k\pi+\pi/3$ ή $x=2k\pi-\pi/3$ με $k\in\mathbb{Z}$

Περισσότερες λυμένες ασκήσεις μπορείτε να βρείτε εδώ.

Επίλυση της τριγωνομετρικής εξίσωσης ημχ=α

Έχουμε δει σε προηγούμενο άρθρο ότι εξίσωση είναι μια ισότητα που περιέχει τουλάχιστον έναν άγνωστο. Αν όμως ο άγνωστος είναι «φυλακισμένος» μέσα σε κάποιο τριγωνομετρικό αριθμό (ημίτονο, συνημίτονο, εφαπτομένη ή συνεφαπτομένη) τότε έχουμε μια ειδική κατηγορία εξισώσεων που λέγονται τριγωνομετρικές εξισώσεις. Παράδειγμα η εξίσωση $2\sigma\upsilon\nu(x)=-1$ και η $\epsilon\phi(2x+\frac{\pi}{3})=1$ είναι τριγωνομετρικές εξισώσεις αφού το x είναι κλεισμένο μέσα σε τριγωνομετρικό αριθμό, ενώ η εξίσωση $2\epsilon\phi(\frac{\pi}4)=x+1$ δεν είναι γιατί παρότι υπάρχει ενας τριγωνομετρικός αριθμός, ο άγνωστος x κυκλοφορεί ελύθερος.

Παράδειγμα

Μια τριγωνομετρική εξίσωση όπως η $\eta\mu\chi=\frac{1}2$ μας ρωτάει: «ποια γωνία έχει ημίτονο ίσο με 1/2;» Η πρώτη γωνία που μας έρχεται στο μυαλό είναι η π/6 (=30^ο). Είναι όμως η μοναδική γωνία που έχει ημίτονο ισο με 1/2; Η απάντηση αν το σκεφτούμε λίγο είναι προφανώς όχι αφού εκτός από τη γωνία π/6 και η γωνία π-π/6 (=5π/6=150^ο) ,που είναι η παραπληρωματική της π/6, έχει ημίτονο ίσο με 1/2. Θυμηθείτε ότι οι παραπληρωματικές γωνίες έχουν ίδιο ημίτονο ( το μάθαμε στο Γυμνάσιο ) πράγμα που φαίνεται από τον τριγωνομετρικό κύκλο (ρίξτε μια ματιά στην εικόνα) αλλά και από τη γραφική παράσταση του ημιτόνου. Αλλά κι όλες οι γωνίες που (ανεξαρτήτως πόσες στροφές έχουμε κάνει στον τριγωνομετρικό κύκλο) καταλήγουν στο π/6 ή στο π-π/6, έχουν κι αυτές ημίτονο ίσο με 1/2.

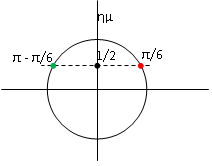
Δηλαδή

	0 στροφές+π/6	1 στροφή+π/6	2 στροφές+π/6	3 στροφές+π/6	k στροφές +π/6
χ	π/6	2π+π/6	2(2π)+π/6	3(2π)+π/6	k(2π)+π/6
ημχ	1/2	1/2	1/2	1/2	1/2

	0 στροφές+(π-π/6)	1 στροφή+(π-π/6)	2 στροφές+(π-π/6)	3 στροφές+(π-π/6)	k στροφές +(π-π/6)
χ	(π-π/6)	2π+(π-π/6)	2(2π)+(π-π/6)	3(2π)+(π-π/6)	k(2π)+(π-π/6)
ημχ	1/2	1/2	1/2	1/2	1/2

Βλέπουμε λοιπόν ότι υπάρχουν άπειρες γωνίες με ημίτονο 1/2, χωρισμένες σε δύο ομάδες, αυτές που καταλήγουν στο π/6 και αυτές που καταλήγουν στο (π-π/6), ‘ετσι αν θέλαμε να τις γράψουμε όλες αναλυτικά δεν θα μπορούσαμε. Μπορούμε όμως να τις περιγράψουμε και να πούμε ότι: χ=2kπ+π/6 ή χ=2kπ+(π-π/6), όπου το k είναι ακέραιος αριθμός (στην πραγματικότητα το k είναι «μετρητής στροφών» ,

για k=0 παίρνουμε τις γωνίες π/6 και π-π/6=5π/6,

για k=1 εχουμε κάνει μια στροφή και έχουμε καταλήξει στα σημεία π/6 και π-π/6 άρα έχουμε τις γωνίες 2π+π/6 και 2π+(π-π/6)=2π+5π/6 κ.ο.κ. δηλαδή

	k=-2	k=-1	k=0	k=1	k=2
χ	-4π+π/6	-2π+π/6	π/6	2π+π/6	4π+π/6
χ	-4π+5π/6	-2π+5π/6	5π/6	2π+5π/6	4π+5π/6

Γενίκευση

Μην ξεχνάτε ότι μέχρι εδώ ασχοληθήκαμε μόνο με ένα παράδειγμα, δηλαδή λύναμε την τριγωνομετρική εξίσωση $\eta\mu\chi=1/2$ . Τώρα ήρθε η ώρα να το γενικεύσουμε λίγο: Αν είχαμε να λύσουμε μια εξίσωση της μορφής

$\eta\mu\chi=\alpha$

θα έπρεπε να βρούμε μια γωνία από τον πρώτο κύκλο που να ικανοποιούσε αυτή την ισότητα (μια αρχική λύση ας πούμε), δηλαδή να βρούμε μια γωνία που να έχει ημίτονο ίσο με α. Έστω ότι την βρήκαμε κι η γωνία αυτή είναι η θ (πρέπει δηλαδή να ισχύει ημθ=α), τότε

οι λύσεις της
$\eta\mu\chi=\alpha\Leftrightarrow\eta\mu\chi=\eta\mu\theta$

θα είναι
$\chi=2k\pi+\theta , \chi=2k\pi+(\pi-\theta)$

Κάντε κλικ να δείτε και τις υπόλοιπες τριγωνομετρικές εξισώσεις καθώς και λυμένες ασκήσεις .

Επίλυση δευτεροβάθμιας εξίσωσης

Continue reading «Επίλυση δευτεροβάθμιας εξίσωσης»

Θέλω να μάθω … πως να βρίσκω τις λύσεις σε μια εξίσωση 2ου βαθμού

Εξίσωση 2ου βαθμού (ή δευτεροβάθμια εξίσωση) είναι η εξίσωση που περιέχει έναν άγνωστο (π.χ. τον x) και έχει ή μπορεί να πάρει τη μορφή $\alpha\chi^2+\beta\chi+\gamma=0$ με $\alpha\neq0$ .

Όταν μας δώσουν μια εξίσωση για να βρούμε τις λύσεις της και δεν είναι στη παραπάνω μορφή δεν γνωρίζουμε αν πράγματι είναι δευτεροβάθμια εξίσωση ή όχι. Γι’ αυτό είμαστε υποχρεωμένοι να κάνουμε κάποια «προεργασία» ώστε να είμαστε σε θέση να αντιληφθούμε το βαθμό της εξίσωσης και κατόπιν να ψάξουμε να βρούμε τις λύσεις. Γιατί με άλλο τρόπο δουλεύουμε στις εξισώσεις πρώτου βαθμού, με άλλο σε αυτές που είναι δεύτερου βαθμού, διαφορετικά στις τριτοβάθμιες κ.ο.κ. Όσον αφορά στις πρωτοβάθμιες εξισώσεις έχουμε δώσει τη μεθοδολογία εδώ.

Η «προεργασία» λοιπόν που πρέπει να γίνει είναι ήδη γνωστή, θα πρέπει:

να απαλλάξουμε την εξίσωση από τους παρονομαστές που τυχόν έχει

(πολλαπλασιάζοντας όλους τους όρους με το ΕΚΠ των παρονομαστών)

να διώξουμε τις παρενθέσεις
(με χρήση της επιμεριστικής ιδιότητας) και τέλος
να κάνουμε αναγωγή όμοιων όρων
(να «συμμαζέψουμε» την εξίσωση προσθέτοντας μεταξύ τους τους όμοιους όρους)

Σε αυτό το σημείο είμαστε σε θέση να δούμε το βαθμό της εξίσωσης και αν

ο άγνωστος δεν είναι υψωμένος σε καμία δύναμη, τότε έχουμε να λύσουμε μια πρωτοβάθμια εξίσωση κατά τα γνωστά (χωρίζουμε γνωστούς – άγνωστους κ.τ.λ.)
η μεγαλύτερη δύναμη στην οποία εμφανίζεται ο άγνωστος είναι το τετράγωνο, τότε είμαστε στη περίπτωση της δευτεροβάθμιας εξίσωσης και η διαδικασία που ακολουθούμε για να βρούμε τις λύσεις είναι η παρακάτω:

Μεταφέρουμε όλους τους όρους στο ένα μέλος ώστε η εξίσωση να πάρει τη μορφή
$\alpha\chi^2+\beta\chi+\gamma=0$
Ξεκαθαρίζουμε ποιοι αριθμοί παίζουν το ρόλο των α, β και γ (α: ο συντελεστής του χ², β: ο συντελεστής του χ και γ ο σταθερός όρος).
Με τη βοήθεια των α, β, γ και του τύπου
$\Delta=\beta^2-4\alpha\gamma$

υπολογίζουμε ένα νέο αριθμό τον Δ που λέγεται «Διακρίνουσα» (διάβασε το Σχόλιο1 παρακάτω)
Από το «είδος» αυτού του αριθμού, του Δ, εξαρτάται κα το πως θα προχωρήσουμε παρακάτω. Και πιο συγκεκριμένα:
- αν η Διακρίνουσα (Δ) είναι αρνητικός αριθμός, τότε η εξίσωση μας δεν έχει λύσεις, είναι όπως λέμε σε τέτοιες περιπτώσεις αδύνατη
- αν η Διακρίνουσα (Δ) είναι θετικός αριθμός, τότε η εξίσωση έχει 2 λύσεις διαφορετικές μεταξύ τους και που τις υπολογίζουμε από τους τύπους
  $\chi_1=\frac{-\beta-\sqrt{\Delta}}{2\alpha}$
  
  και
  $\chi_2=\frac{-\beta+\sqrt{\Delta}}{2\alpha}$
  
  (διάβασε το Σχόλιο2)
- αν η Διακρίνουσα (Δ) είναι ίση με 0, τότε η εξίσωση έχει δύο ίσες λύσεις (ή όπως συνήθως λέμε μια διπλή λύση) που μπορούμε να υπολογίσουμε από τον τύπο
  $\chi_1=\chi_2=\frac{-\beta}{2\alpha}$
  
  (Σχόλιο3)

Συνοπτικά η διαδικασία που ακολουθούμε ώστε να βρούμε τις λύσεις σε μια εξίσωση της μορφής

$\alpha\chi^2+\beta\chi+\gamma=0$

καθώς και οι περιπτώσεις που μπορούν να προκύψουν φαίνονται στο σχήμα που ακολουθεί:

Λυμένα παραδείγματα για να κατανοήσουμε καλύτερα αυτά που αναφέραμε θα δείτε στο επόμενο άρθρο.

Σχόλιο1:

Η παράσταση $\beta^2-4\alpha\gamma$ συμβολίζεται με Δ και λέγεται «Διακρίνουσα». Η ονομασία δεν είναι τυχαία γιατί η διακρίνουσα μας βοηθάει να διακρίνουμε το πλήθος των ριζών (λύσεων) της εξίσωσης. Πράγματι,

Δ<0 $\Leftrightarrow$ 0 λύσεις
Δ=0 $\Leftrightarrow$ 1 λύση διπλή
Δ>0 $\Leftrightarrow$ 2 λύσεις διαφορετικές

Επιστροφή

Σχόλιο2:

Οι δύο αυτοί τύποι μπορούν να γραφούν σε έναν πιο συμμαζεμένο:

$\chi_1,\chi_2=\frac{-\beta\pm\sqrt{\Delta}}{2a}$

Επιστροφή

Σχόλιο3:

Στην πραγματικότητα ο τύπος αυτός δεν είναι κάποιος νέος τύπος που πρέπει να απομνημονεύσουμε αρκεί να ξέρουμε απ’ έξω τον προηγούμενο τύπο αφού από εκεί προκύπτει και αυτός μόνο που τώρα το Δ είναι 0. Πράγματι,

$\chi=\frac{-\beta\pm\sqrt{\Delta}}{2\alpha}=\frac{-\beta\pm\sqrt{0}}{2\alpha}=\frac{-\beta\pm0}{2\alpha}=\frac{-\beta}{2\alpha}$

Επιστροφή

Θέλω να μάθω … πως λύνεται μια εξίσωση 1ου βαθμού

Μεθοδολογία επίλυσης εξίσωσης 1ου βαθμού και λυμένο παράδειγμα.

Κατ’ αρχάς να ξεκινήσουμε από τον τίτλο του άρθρου που είναι λάθος, γιατί αυτό που θα δούμε σ αυτή τη δημοσίευση είναι η διαδικασία που ακολουθούμε ώστε να βρούμε τη λύση μιας εξίσωσης 1ου βαθμού και αυτή (η διαδικασία) λέγεται επίλυση κι όχι λύση (το τι είναι λύση το έχουμε γράψει εδώ).

Ας δούμε λοιπόν ποια βήματα πρέπει να ακολουθούμε ώστε να βρίσκουμε σε οποιαδήποτε εξίσωση 1ου βαθμού, αν έχει λύση και ποια είναι αυτή ή αν δεν έχει λύσεις (αδύνατη). Σκοπός μας είναι μέσα από τη διαδικασία που θα ακολουθήσουμε, σε οποιαδήποτε πρωτοβάθμια εξίσωση κι αν μας έχει δοθεί, να καταλήξουμε στη πιό απλή μορφή εξίσωσης που υπάρχει και είναι αυτή:

$\alpha\cdot\chi=\beta$ , όπου το $\alpha$ και το $\beta$ μπορεί να είναι οποιοσδήποτε αριθμός

Με τέσσερα απλά βήματα (στη χειρότερη περίπτωση) μπορούμε να καταλήξουμε στη μορφή $\alpha\cdot\chi=\beta$ . Τα βήματα είναι τα παρακάτω που θα τα δούμε λύνοντας ταυτόχρονα κι ένα παράδειγμα:

Continue reading «Θέλω να μάθω … πως λύνεται μια εξίσωση 1ου βαθμού»

Θέλω να μάθω…πως διώχνω τους παρονομαστές από μια εξίσωση

Απαλοιφή παρονομαστών

Η διαδικασία που ακολουθούμε ώστε να «διώξουμε» τους παρονομαστές από μια ισότητα, λέγεται απαλοιφή παρονομαστών.

Αν λοιπόν είμαστε άτυχοι κι η εξίσωσή μας έχει παρονομαστές θα πρέπει να τους διώξουμε για να … «κάνουμε τη ζωή μας πιο εύκολη». Το να «εξουδετερώσεις» ή να «εξαφανίσεις» ένα παρονομαστή που εμφανίζεται σε μια ισότητα (ή σε μια εξίσωση, αφού κι αυτή ισότητα είναι) είναι πολύ εύκολη υπόθεση , αρκεί ένας πολλαπλασιασμός.

Για να διώξεις για παράδειγμα τον παρονομαστή 2, αρκεί να πολλαπλασιάσεις όλους τους όρους της ισότητας (στο πρώτο και στο δεύτερο μέλος) με το 2. Δείτε ένα παράδειγμα,

η $x+\frac{3}2=5x$ πολλαπλασιαζόμενη με το 2 γίνεται

$2x+2\cdot\frac{3}2=2\cdot5x$

$\Leftrightarrow2x+3=10x$

που είναι πλέον απαλλαγμένη από παρονομαστές.

Είναι προφανές ότι μπορούσαμε να πετύχουμε το σκοπό μας πολλαπλασιάζοντας όχι μόνο με το 2 αλλά με οποιοδήποτε από τα πολλαπλάσια του 2 όπως 4,6,8,…, επιλέξαμε όμως το μικρότερο για να έχουμε στην νέα εξίσωση που προκύπτει τους μικρότερους δυνατούς συντελεστές. Επίσης είναι προφανές ότι αν ήθελα να «εξαφανίσω» το 3, το 5 κ.ο.κ. από κάποιον παρονομαστή θα διάλεγα να πολλαπλασιάσω με το 3 ή το 5 αντίστοιχα.

Ένα εύλογο ερώτημα που μπαίνει εδώ είναι τι θα κάναμε αν είχαμε δύο ή περισσότερους διαφορετικούς παρονομαστές; Ας υποθέσουμε ότι θέλουμε να εξουδετερώσουμε το 2 και το 3. Η απάντηση είναι απλή και λογική (όπως απλά και λογικά είναι πάντα τα μαθηματικά): Θα πολλαπλασιάζαμε και με το 2 και με το 3 ταυτόχρονα, ή με άλλα λόγια θα πολλαπλασιάζαμε με το 6 (6 = 2.3). Και πάλι τονίζουμε ότι τη δουλεία μας μπορούσαμε να τη κάνουμε όχι μόνο με το 6 αλλά και με τους 12,18,24,…(πολλαπλάσια του 6) δηλαδή με κάθε κοινό πολλαπλάσιο των παρονομαστών 2 και 3. Εμείς όμως διαλέγουμε το μικρότερο κοινό πολλαπλάσιο, το Ε.Κ.Π. δηλαδή, γιατί «έτσι μας συμφέρει». Δείτε το,

$\frac{x}3+\frac{3}2=5x\Leftrightarrow$

$2\cdot3\cdot\frac{x}3+2\cdot3\cdot\frac{3}2=2\cdot3\cdot5x\Leftrightarrow$

$2x+3\cdot3=2\cdot3\cdot5x\Leftrightarrow$

$2x+9=30x$

Επομένως συνοψίζοντας,

[gn_box title=»tip» type=»info»] για να διώξουμε τους παρονομαστές από μια εξίσωση, πολλαπλασιάζουμε όλους τους όρους της εξίσωσης με το Ε.Κ.Π. των παρονομαστών.[/gn_box]

πως μας βοηθά η παραγοντοποίηση στην επίλυση εξισώσεων δεύτερου βαθμού ή μεγαλύτερου.

Τι είναι λοιπόν η απόλυτη τιμή;

Ας δούμε τώρα τι γίνεται με τις εξισώσεις.

Άσκηση 1: Να λυθεί η εξίσωση

Άσκηση 2: Να λυθεί η εξίσωση

Άσκηση 3: Να βρεθούν οι αριθμοί που ικανοποιούν τη σχέση

Άσκηση 4: Να βρεθούν οι αριθμοί που ικανοποιούν τη σχέση

Βήμα 10

Βήμα 20

Βήμα 30

Τύποι λύσεων για τριγωνομετρικές εξισώσεις

Παράδειγμα

Γενίκευση

Απαλοιφή παρονομαστών

Άσκηση 1: Να λυθεί η εξίσωση $\frac{4-5|x|}{12}-\frac{3|x|-3}{2}=2|-x|-6$

Άσκηση 2: Να λυθεί η εξίσωση $\frac{4-5|x-1|}{12}-\frac{3|x-1|-3}{2}=2|1-x|-6$

Άσκηση 3: Να βρεθούν οι αριθμοί που ικανοποιούν τη σχέση $2-|x|=x^2$

Άσκηση 4: Να βρεθούν οι αριθμοί που ικανοποιούν τη σχέση $|2x+3|=|x+9|$

Βήμα 1⁰

Βήμα 2⁰

Βήμα 3⁰