
Quiz Γ΄ Γυμνασίου: Ταυτότητες
Λύστε ένα κουίζ με ασκήσεις Σωστού – Λάθους, Πολλαπλής Επιλογής, Αντιστοίχισης κ.α. με ερωτήσεις από τις Ταυτότητες
a magic land
Λύστε ένα κουίζ με ασκήσεις Σωστού – Λάθους, Πολλαπλής Επιλογής, Αντιστοίχισης κ.α. με ερωτήσεις από τις Ταυτότητες

Στην Β΄ Γυμνασίου μάθαμε έναν αλγόριθμο (μεθοδολογία) για να επιλύουμε κάθε εξίσωση πρώτου βαθμού.
Τώρα στη Τρίτη τάξη θα δούμε πως μπορούμε κάτω από ορισμένες συνθήκες να βρούμε τις λύσεις και σε άλλες εξισώσεις μεγαλύτερου βαθμού. Η μέθοδος αυτή δεν αποδίδει πάντα, γι’ αυτό αργότερα θα την συμπληρώσουμε
Πριν όμως από αυτό θα πρέπει να δούμε μια σημαντική ιδιότητα:
![Rendered by QuickLaTeX.com \[A \cdot\ B=0\Leftrightarrow \left \{ \begin{matrix} A=0\\ \eta\\ B=0 \end{matrix} \right.\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-94a3e97ff683988e71bf7dccfb4717e3_l3.png)
Η οποία μας λέει ότι ένα γινόμενο είναι ίσο με μηδέν τότε και μόνο τότε αν τουλάχιστον ένας από τους παράγοντες του γινομένου είναι ίσος με μηδέν.
Να δούμε τώρα λύνοντας ένα παράδειγμα πως μπορούμε να εκμεταλλευτούμε τα παραπάνω για να βρούμε τις λύσεις σε μια εξίσωση 2ου βαθμού. Έστω λοιπόν ότι ψάχνουμε να βρούμε εκείνους τους αριθμούς που ικανοποιούν τη σχέση ![]() . Αυτή είναι μια δευτεροβάθμια εξίσωση την οποία και θα μετατρέψω σε γινόμενο (με κάποια από τις μεθόδους παραγοντοποίησης που μάθαμε) με σκοπό να χρησιμοποιήσω την ιδιότητα που προαναφέραμε. Έτσι έχουμε
. Αυτή είναι μια δευτεροβάθμια εξίσωση την οποία και θα μετατρέψω σε γινόμενο (με κάποια από τις μεθόδους παραγοντοποίησης που μάθαμε) με σκοπό να χρησιμοποιήσω την ιδιότητα που προαναφέραμε. Έτσι έχουμε
![]()
(βγάζουμε κοινό παράγοντα το x)
![]()
φτάσαμε λοιπόν στο σημείο να έχουμε ένα γινόμενο που είναι ίσο με το μηδέν. Το γινόμενο αυτό αποτελείται από δύο (πρωτοβάθμιους) παράγοντες τον x και τον x-1. Σύμφωνα με την ιδιότητα που αναφέραμε παραπάνω συμπεραίνουμε ότι τουλάχιστον ένας από αυτούς τους παράγοντες θα είναι ίσος με μηδέν. Δηλαδή θα ισχύει:
![Rendered by QuickLaTeX.com \[\left \{ \begin{matrix} x=0\\ \eta\\ x-1=0\Leftrightarrow x=1 \end{matrix} \right.\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-e0bf973469422918d9d4517961478978_l3.png)
Από τον τρόπο που λύθηκε το προηγούμενο παράδειγμα φαίνεται το ποια μέθοδο πρέπει ν’ ακολουθούμε για να επιλύσουμε μια εξίσωση που έχει βαθμό μεγαλύτερο του πρώτου:
[su_label style=»important»]Βήμα 1ο:[/su_label] Μεταφέρουμε όλους τους όρους στο α’ μέλος έτσι ώστε στο δεύτερο μέλος να είναι ίσο με μηδέν.
[su_label style=»success»]Βήμα 2ο:[/su_label] Μετατρέπουμε σε γινόμενο το α’ μέλος.
[su_label style=»warning»]Βήμα 3ο:[/su_label] Παίρνουμε κάθε παράγοντα του γινομένου ίσο με μηδέν.
[su_label style=»info»]Βήμα 4ο:[/su_label] Λύνουμε κάθε μια από τις εξισώσεις (1ου βαθμού) που προκύπτουν από το προηγούμενο βήμα.
Στο άρθρο αυτό θα ασχοληθούμε με:
[wptabs mode=»horizontal»]
[wptabtitle]Φυσικοί[/wptabtitle]
[wptabcontent]
 Οι αριθμοί 0,1,2,3,4,5,6,7,8,9,10,11,…,2012,…,3150,… λέγονται φυσικοί αριθμοί.
Οι αριθμοί 0,1,2,3,4,5,6,7,8,9,10,11,…,2012,…,3150,… λέγονται φυσικοί αριθμοί.
Δηλαδή,
Φυσικός αριθμός είναι οποιοσδήποτε αριθμός μπορεί να γραφεί μόνο με τη βοήθεια των ψηφίων 0,1,2,3,4,5,6,7,8 και 9.
Για να γράψουμε έναν οποιοδήποτε φυσικό χρησιμοποιούμε τα ψηφία 0,1,2,3,4,5,6,7,8,9. Αυτό το πετυχαίνουμε γιατί στο δεκαδικό σύστημα αρίθμησης η αξία ενός ψηφίου αλλάζει ανάλογα με τη θέση του μέσα στον αριθμό. Έτσι στους παρακάτω αριθμούς το ψηφίο 3 δηλώνει:
στον 123, 3 μονάδες
στον 1234, 3 δεκάδες ή 30 μονάδες (3.10 )
ενώ στον 12345, 3 εκατοντάδες ή 300 μονάδες (3.100)
[/wptabcontent]
[wptabtitle]Σύγκριση[/wptabtitle]
[wptabcontent]
Σύγκριση δύο αριθμών είναι η εξέτασή τους για τον καθορισμό του ποιος είναι μεγαλύτερος, ποιος μικρότερος ή αν αυτοί είναι ίσοι.
Έτσι αν έχουμε δύο φυσικούς αριθμούς έστω ν και μ θα γράφουμε:
ν=μ, αν οι αριθμοί είναι ίσοι
ν>μ, αν ο ν είναι μεγαλύτερος του μ
ν<μ, αν ο ν είναι μικρότερος του μ.
Πάνω σε μια ευθεία επιλέγουμε τυχαίο σημείο που ονομάζουμε Ο κι αντιστοιχούμε σε αυτό τον αριθμό 0.
Έπειτα επιλέγουμε και πάλι τυχαία δεξιά από το Ο ένα άλλο σημείο Α στο οποίο αντιστοιχούμε τον αριθμό 1.  Στη συνέχεια χρησιμοποιώντας σαν μονάδα μέτρησης το ευθύγραμμο τμήμα ΟΑ ορίζουμε διαδοχικά τμήματα ίσα με το ΟΑ, δηλαδή ΟΑ=ΑΒ=ΒΓ=ΓΔ κ.τ.λ.. Τώρα το σημείο Β παριστάνει τον αριθμό 2, το Γ τον αριθμό 3 κ.λ.π. Η ευθεία αυτή που κατασκευάσαμε ονομάζεται άξονας των φυσικών αριθμών. Κάθε φυσικός αριθμός τώρα αντιστοιχεί σε ένα και μοναδικό σημείο.][/wptabcontent]
Στη συνέχεια χρησιμοποιώντας σαν μονάδα μέτρησης το ευθύγραμμο τμήμα ΟΑ ορίζουμε διαδοχικά τμήματα ίσα με το ΟΑ, δηλαδή ΟΑ=ΑΒ=ΒΓ=ΓΔ κ.τ.λ.. Τώρα το σημείο Β παριστάνει τον αριθμό 2, το Γ τον αριθμό 3 κ.λ.π. Η ευθεία αυτή που κατασκευάσαμε ονομάζεται άξονας των φυσικών αριθμών. Κάθε φυσικός αριθμός τώρα αντιστοιχεί σε ένα και μοναδικό σημείο.][/wptabcontent]
[wptabtitle]Στρογγυλοποίηση[/wptabtitle]
[wptabcontent]
Στρογγυλοποίηση, λέμε τη διαδικασία με την οποία αντικαθιστούμε ένα φυσικό αριθμό με κάποιον άλλο λίγο μεγαλύτερό του ή λίγο μικρότερό του.
Για τη στρογγυλοποίηση των αριθμών ακολουθούμε τα παρακάτω βήματα και δεν την κάνουμε «όπως μας συμφέρει»
βήμα 1:
επιλέγουμε την τάξη του ψηφίου στην οποία θα κάνουμε την στρογγυλοποίηση (π.χ. Μονάδες, Δεκάδες κτλ)
βήμα 2:
παράδειγμα: αν τον αριθμό 31812 θέλουμε να τον στρογγυλοποιήσουμε στη εκατοντάδα (ψηφίο 8), κοιτάμε το επόμενο στα δεξιά ψηφίο ( το 1 που είναι μικρό). Ξαναγράφουμε λοιπόν τον αριθμό μας αντικαθιστώντας όλα τα ψηφία που βρίσκονται δεξιότερα του 8 με μηδενικά κι έχουμε τον νέο στρογγυλοποιημένο αριθμό 31800.
παράδειγμα: αν τον αριθμό 31812 θέλουμε να τον στρογγυλοποιήσουμε στην χιλιάδα (ψηφίο 1), κοιτάμε το επόμενο προς τα δεξιά ψηφίο (το 8 που είναι μεγάλο). Ξαναγράφουμε λοιπόν τον αριθμό μας αυξάνοντας το 1 και κάνοντας το 2 κι όλα τα δεξιότερα ψηφία γίνονται μηδενικά. Έτσι έχουμε το νέο αριθμό 32000.
Η στρογγυλοποίηση γίνεται για πρακτικούς λόγους και η τάξη στην οποία κάνουμε στρογγυλοποίηση εξαρτάται από το τι παριστάνει ο αριθμός αυτός. Για παράδειγμα αν αναφερθούμε στον αριθμό των θεατών που παρακολούθησαν τη συναυλία της Madonna στην Αθήνα δεν θα πούμε 82.345 αλλά 82.000 θεατές(στρογγυλοποίηση στη χιλιάδα). Επίσης αν ο μέσος μισθός ενός υπαλλήλου μιας επιχείρησης είναι 1345€ μπορούμε να πούμε ότι είναι 1300€ (στρογγυλοποίηση στην εκατοντάδα). Υπάρχουν όμως και αριθμοί που δεν επιτρέπεται να στρογγυλοποιήσουμε όπως οι αριθμοί που ταυτοποιούν αντικείμενα για παράδειγμα οι ταχυδρομικοί κώδικες, αριθμοί τηλεφώνων κ.α. [/wptabcontent] [/wptabs]
Ο ορισμός και οι ιδιότητες των δυνάμεων. Τι είναι η «βάση» και τι ο «εκθέτης»;
Σε περίπτωση που σε μια παράσταση έχουμε να εκτελέσουμε πολλές πράξεις, ποια από αυτές προηγείται;
 Πολλές φορές συναντάμε γινόμενα στα οποία όλοι οι παράγοντες είναι μεταξύ τους ίσοι. Στις περιπτώσεις αυτές χρησιμοποιήσουμε πιο εύχρηστα σύμβολα, αυτά των δυνάμεων. Έτσι συμφωνήσαμε τα εξής:
Πολλές φορές συναντάμε γινόμενα στα οποία όλοι οι παράγοντες είναι μεταξύ τους ίσοι. Στις περιπτώσεις αυτές χρησιμοποιήσουμε πιο εύχρηστα σύμβολα, αυτά των δυνάμεων. Έτσι συμφωνήσαμε τα εξής:
• Το γινόμενο ![]() που αποτελείται από ν παράγοντες ίσους με α συμβολίζεται με αν και ονομάζεται ν-οστή δύναμη του α (διαβάζεται α εις την ν ). Ο αριθμός α λέγεται βάση της δύναμης ενώ το ν ονομάζεται εκθέτης και μας δείχνει πόσες φορές θα «επαναλάβουμε» τον αριθμό α στο γινόμενο.
που αποτελείται από ν παράγοντες ίσους με α συμβολίζεται με αν και ονομάζεται ν-οστή δύναμη του α (διαβάζεται α εις την ν ). Ο αριθμός α λέγεται βάση της δύναμης ενώ το ν ονομάζεται εκθέτης και μας δείχνει πόσες φορές θα «επαναλάβουμε» τον αριθμό α στο γινόμενο.
Παράδειγμα: Ο συμβολισμός 34 (διαβάζεται 3 στην τετάρτη) και παριστάνει το γινόμενο ![]() , δηλαδή τον αριθμό 81 .
, δηλαδή τον αριθμό 81 .
• Ειδικά η δύναμη α2 (α στη δευτέρα) διαβάζεται και α στο τετράγωνο, ενώ για τη δύναμη α3 (α στην τρίτη) μπορούμε να διαβάζουμε και α στον κύβο. (γιατί;)
• Η πρώτη δύναμη του αριθμού α είναι ο ίδιος ο αριθμός α, δηλαδή ισχύει: α1 = α και προφανώς ισχύει ότι: 1ν = 1 .
• Για τις δυνάμεις του 10 έχουμε τον παρακάτω κανόνα:

Στον υπολογισμό αριθμητικών παραστάσεων η σειρά με την οποία εκτελούνται οι πράξεις είναι η παρακάτω:
| 1. Δυνάμεις | |
| 2. Πολλαπλασιασμοί και Διαιρέσεις | (όποιο συναντάμε πρώτο) |
| 3. Προσθέσεις κι Αφαιρέσεις | (όποιο συναντάμε πρώτο) |
• Στην περίπτωση που στην αριθμητική παράσταση υπάρχουν παρενθέσεις, ξεκινάμε τις πράξεις πρώτα μέσα από τις παρενθέσεις πάντα όμως με την παραπάνω σειρά.
Οι ιδιότητες της πρόσθεσης, της αφαίρεσης και του πολλαπλασιασμού στο σύνολο των Φυσικών Αριθμών. Παρουσιάζεται και η πολλή σημαντική επιμεριστική ιδιότητα του πολλαπλασιασμού ως προς την πρόσθεση και την αφαίρεση.
Πρόσθεση είναι η πράξη με την οποία από δύο φυσικούς αριθμούς α και β (που παριστάνουν πλήθος όμοιων αντικειμένων) βρίσκουμε ένα τρίτο φυσικό γ που είναι το άθροισμά τους (και παριστάνει το συνολικό πλήθος των αντικειμένων)
Οι αριθμοί α και β λέγονται προσθετέοι, ένω ο γ λέγεται άθροισμα των α και β και μπορεί να συμβολιστεί και ως α+β,δηλαδή ισχύει α+β=γ.
| α+β=β+α | Μπορούμε να αλλάξουμε τη σειρά των δύο προσθετέων σ’ ένα άθροισμα | Αντιμεταθετική |
| α+(β+γ)=(α+β)+γ | Μπορούμε να αντικαταστήσουμε δύο προσθετέους με το άθροισμά τους | Προσεταιριστική |
| α+0=α | Το 0 όταν προστεθεί σε οποιοδήποτε φυσικό αριθμό δεν τον μεταβάλλει | Ουδέτερο στοιχείο |
Η αντιμεταθετική ιδιότητα σε συνδυασμό με την προσεταιριστική μας δίνουν το δικαίωμα να προσθέτουμε τους φυσικούς αριθμούς με οποιαδήποτε σειρά μας «βολεύει». Έτσι για την παρακάτω πρόσθεση θα μπορούσαμε να κάνουμε τα εξής:
45+13+8+22+55+87+70=
(45+55)+(13+87)+(8+22+70)=
100+100+100=300.

Αφαίρεση δύο αριθμών μ (=μειωτέος) και α (=αφαιρετέος) είναι η πράξη με την οποία βρίσκουμε ένα άλλο αριθμό δ (=διαφορά) που αν προστεθεί στον α μας δίνει τον μ.
Δηλαδή:
μ – α = δ μόνο αν ισχύει δ+α=μ, με μ>α
Προσοχή, στην αφαίρεση των φυσικών αριθμών δεν επιτρέπεται η αλλαγή στη σειρά τους διότι η πράξη δεν μπορεί να εκτελεστεί.
Δηλαδή εδώ δεν ισχύει ούτε η αντιμεταθετική ιδιότητα ούτε η προσεταιριστική.
Πολλαπλασιασμός, είναι η πράξη που από δύο φυσικούς αριθμούς α και β, βρίσκουμε ένα τρίτο φυσικό αριθμό γ που είναι το γινόμενό τους και συμβολίζεται με ![]() Δηλαδή:
Δηλαδή: ![]()
Οι αριθμοί α και β λέγονται παράγοντες του γινομένου.
|
|
Μπορούμε να αλλάξουμε τη σειρά των δύο παραγόντων σ’ ένα γινόμενο | Αντιμεταθετική |
|
|
Μπορούμε να αντικαταστήσουμε δύο παράγοντες με το γινόμενό τους | Προσεταιριστική |
|
|
Το 1 όταν πολλαπλασιαστεί με οποιοδήποτε φυσικό αριθμό δεν τον μεταβάλλει | Ουδέτερο στοιχείο |
|
|
Ότι πολλαπλασιάζεται με το 0 μηδενίζεται | Απορροφητικό στοιχείο |
Επιμεριστική ιδιότητα του πολλαπλασιασμού ως προς τη πρόσθεση και την αφαίρεση:
Μια πολλή σημαντική ιδιότητα που συνδέει τον πολλαπλασιασμό με την πρόσθεση (και την αφαίρεση). Η ιδιότητα αυτή μας δίνει το δικαίωμα να υπολογίζουμε την τιμή κάποιας παράστασης με δύο τρόπους.
Επιμεριστική ιδιότητα:
![]()
![]()
Ξέρουμε τον τύπο της συνάρτησης f και θέλουμε να βρούμε τα κοινά σημεία της γραφικής παράστασης της f με τους άξονες x’x και y’y.
ΑΛΓΕΒΡΑ Α΄ ΛΥΚΕΙΟΥ
 Όταν μας δίνεται ο τύπος μιας συνάρτησης στην ουσία μας δίνεται μια σχέση (ισότητα) που μας δείχνει τον τρόπο που συνδέονται μεταξύ τους τα x (=πρότυπα) με τα y (ή αλλιώς f(x)-εικόνες). Έτσι έχουμε τη δυνατότητα όταν γνωρίζουμε το x να μπορούμε να υπολογίσουμε την εικόνα του αλλά και το αντίστροφο όταν μας δίνουν το y μπορούμε εμείς να βρούμε το x. Ας πάρουμε για παράδειγμα τη συνάρτηση f με τύπο f(x)=4-x2. Για να βρω την εικόνα του 1 δεν έχω παρά να βάλω όπου x τον αριθμό 1 και να υπολογίσω το y. Έτσι θα έχω f(1)=4-12=3, δηλαδή η εικόνα του 1 είναι ο αριθμός 3. Αυτό μου δίνει και μια επιπλέον πληροφορία ότι η γραφική παράσταση της συνάρτησης f διέρχεται από το σημείο με συντεταγμένες (1,3). Αν τώρα μας ρωτήσουν ποιος αριθμός έχει εικόνα το -12 θα πρέπει εμείς να πάμε και πάλι στον τύπο της συνάρτησης και να βάλουμε όπου y (ή f(x) – το ίδιο είναι) τον αριθμό -12 και από τη σχέση αυτή να υπολογίσουμε το x. Ας το δούμε,
Όταν μας δίνεται ο τύπος μιας συνάρτησης στην ουσία μας δίνεται μια σχέση (ισότητα) που μας δείχνει τον τρόπο που συνδέονται μεταξύ τους τα x (=πρότυπα) με τα y (ή αλλιώς f(x)-εικόνες). Έτσι έχουμε τη δυνατότητα όταν γνωρίζουμε το x να μπορούμε να υπολογίσουμε την εικόνα του αλλά και το αντίστροφο όταν μας δίνουν το y μπορούμε εμείς να βρούμε το x. Ας πάρουμε για παράδειγμα τη συνάρτηση f με τύπο f(x)=4-x2. Για να βρω την εικόνα του 1 δεν έχω παρά να βάλω όπου x τον αριθμό 1 και να υπολογίσω το y. Έτσι θα έχω f(1)=4-12=3, δηλαδή η εικόνα του 1 είναι ο αριθμός 3. Αυτό μου δίνει και μια επιπλέον πληροφορία ότι η γραφική παράσταση της συνάρτησης f διέρχεται από το σημείο με συντεταγμένες (1,3). Αν τώρα μας ρωτήσουν ποιος αριθμός έχει εικόνα το -12 θα πρέπει εμείς να πάμε και πάλι στον τύπο της συνάρτησης και να βάλουμε όπου y (ή f(x) – το ίδιο είναι) τον αριθμό -12 και από τη σχέση αυτή να υπολογίσουμε το x. Ας το δούμε,
-12=4-x2 άρα 0=16-x2 δηλαδή (4-x)(4+x)=0 οπότε x=4 ή x= -4. Απαντάμε λοιπόν ότι οι αριθμοί -4 , 4 έχουν εικόνα τον -12. Πράγμα που σημαίνει ακόμη ότι η γραφική παράσταση της συνάρτησης f (συμβολίζεται με Cf ) περνάει από τα σημεία (-4,-12) και (4,-12). Τελειώσαμε με την εισαγωγή πάμε τώρα στο θέμα μας.
Θέλουμε να βρούμε τα σημεία που η γραφική παράσταση μιας συνάρτησης τέμνει τον άξονα x’x γνωρίζουμε όμως ότι όλα τα σημεία που βρίσκονται πάνω στον άξονα αυτό έχουν τεταγμένη μηδέν (y=0). Το ίδιο θα ισχύει και με το σημείο που ψάχνουμε άρα αρκεί να βάλουμε στον τύπο της συνάρτησης μας y=0 και να υπολογίσουμε το x. Ας χρησιμοποιήσουμε πάλι την ίδια συνάρτηση που χρησιμοποιήσαμε και πιο πάνω y=4-x2 η οποία για y=0 γίνεται 0=4-x2 δηλαδή 0=(2-x)(2+x) απ’ όπου προκύπτει x=-2 ή x=2. Επομένως γνωρίζουμε τώρα ότι η f τέμνει τον x’x στα σημεία με συντεταγμένες (-2,0) και (2,0)
Για να βρούμε το σημείο(αν υπάρχει θα είναι ένα και μοναδικό) που η γραφική παράσταση μιας συνάρτησης τέμνει τον άξονα y’y αρκεί να σκεφτούμε ότι όλα τα σημεία του άξονα αυτού έχουν τετμημένη ίση με μηδέν (x=0). Έτσι λοιπόν θα βάλουμε κι εμείς στον τύπο της συνάρτησης όπου x το αριθμό 0 και θα βρούμε πολύ εύκολα το y. Στην y=4-x2 για x=0 παίρνω y=4 και γνωρίζω πλέον ότι η f τέμνει τον y’y στο σημείο με συντεταγμένες (0,4).
Μπορούμε τώρα να καταλήξουμε στο παρακάτω συμπέρασμα:
[su_box color=»#0997FC» title=»Τομές γραφικής παράστασης με τους άξονες»][su_list style=»idea»]
Για να βρω που τέμνει η γραφική παράσταση της f
[/su_list][/su_box]
Ας δούμε και μερικά παραδειγματάκια τα οποία σας προτείνω να λύσετε μόνοι σας και στη συνέχεια να κάνετε κλικ στη «Λύση» για να τσεκάρετε αυτό που βρήκατε.
Να βρείτε σε ποιο σημείο τέμνει η
![]()
τον άξονα y’y
[wpspoiler name=»Λύση»]
Η f αν τέμνει τον y’y θα τον τέμνει στο σημείο με συντεταγμένες (0,f(0)). Αρκεί λοιπόν να βρούμε το f(0). Βάζουμε x=0 και έχουμε
![]()
Επομένως το σημείο είναι το (0,1)
Παρατήρηση: Μια συνάρτηση δεν είναι υποχρεωτικό να τέμνει τον άξονα y’y αυτό μπορεί να συμβαίνει για παράδειγμα σε μια συνάρτηση που το 0 δεν θα ανήκει στο πεδίο ορισμού της και κατά συνέπεια δεν θα υπάρχει το f(0) π.χ. η g(x)=1/x. Αν στο πεδίο ορισμού της συνάρτησης υπάρχει το 0 τότε μπορώ να βρω την εικόνα του άρα και το σημείο που τέμνει αυτή τον y’y. Το σημείο αυτό όμως θα είναι μοναδικό γιατί δεν γίνεται να δώσω στο x την τιμή 0 και να πάρω περισσότερα από ένα αποτελέσματα άλλωστε το λέει ξεκάθαρα και ο ορισμός της συνάρτησης ότι «σε κάθε x από το πεδίο ορισμού αντιστοιχεί ένα και μόνο y». Έτσι λοιπόν η γραφική παράσταση μιας συνάρτησης μπορεί να τέμνει τον y’y το πολύ σε ένα σημείο.
[/wpspoiler]
Αν η συνάρτηση
![]()
τέμνει τον y’y σε σημείο με τεταγμένη 1 να βρείτε το k.
[wpspoiler name=»Λύση»]Το σημείο που η f τέμνει τον y’y έχει συντεταγμένες (0,f(0)). Η άσκηση μας δίνει τη πληροφορία ότι το σημείο αυτό είναι το (0,1) άρα είναι «υποχρεωτικό» να ισχύει
![]()
![]()
![]()
![]()
![]()
[/wpspoiler]
Να βρείτε τα σημεία τομής των γραφικών παραστάσεων των συναρτήσεων
![]()
και
![]()
με τους άξονες.
[wpspoiler name=»Λύση»]
![]()
γιατί το x δεν μπορεί να πάρει την τιμή 1 αφού μηδενίζει τον παρονομαστή (x-1=0 ![]() x=1)
x=1)
Τομή με τον y’y: Βάζω x=0 και παίρνω
![]()
άρα τέμνει τον y’y στο (0,-2)
Τομές με τον x’x: Βάζω y=0 και παίρνω
![]()
η εξίσωση αυτή είναι δεύτερου βαθμού με διακρίνουσα αρνητική (Δ=12-4.1.2=-7) επομένως δεν έχει λύσεις πράγμα που σημαίνει ότι η γραφική παράσταση της f δεν τέμνει τον x’x.
Παρατήρηση: Η εξίσωση f(x)=0 είναι μια εξίσωση με άγνωστο το x και το πόσες λύσεις θα έχει εξαρτάται από τη μορφή που θα έχει ο τύπος της συνάρτησης μπορεί να είναι αδύνατη όπως αυτή που είδαμε μόλις τώρα και η Cf να μην τέμνει τον x’x αλλά μπορεί να έχει μια, δύο, τρεις ή και άπειρες λύσεις οπότε να τέμνει τον x’x σε δύο, τρία ή και άπειρα σημεία.
![]()
γιατί το x είναι παρονομαστής και δεν μπορεί να μηδενίζεται
Τομή με τον y’y: Βάζω x=0 ???? Προφανώς η Cg δεν τέμνει τον άξονα των y αφού δεν υπάρχει το g(0)
Τομές με τον x’x: Βάζω y=0 και λύνω την εξίσωση
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\left\{\begin{matrix}4x-12=8\\ \eta \\4x-12=-8 \end{matrix}\Leftrightarrow \left\{\begin{matrix}4x=20\Leftrightarrow x=5\\ \eta \\4x=4\Leftrightarrow x=1\end{matrix}\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-334cae74292529eb6254713ee7ee42a1_l3.png)
επομένως η γραφική παράσταση της g τέμνει τον άξονα x’x στα σημεία (1,0) , (5,0)
[/wpspoiler]
Αν γνωρίζουμε ότι η συνάρτηση
![]()
τέμνει τον y’y στο σημείο με τεταγμένη 6 και τον x’x στα σημεία με τετμημένες 2 και 3 να βρεθούν τα a,b και c.
[wpspoiler name=»Λύση»]
Επειδή η f τέμνει τον y’y στο (0,6) θα πρέπει να ισχύει
![]()
Τώρα η συνάρτηση μας παίρνει τη μορφή
![]()
γνωρίζουμε όμως ότι τέμνει και τον x’x στα (2,0) και (3,0) επομένως θα ισχύει
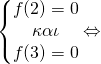
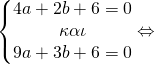
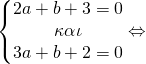
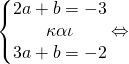
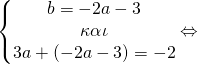
![]()
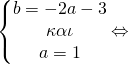
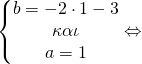
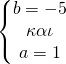
Έτσι μετά τη λύση του συστήματος βρήκαμε a=1, b=-5, c=6 οπότε και η f είναι η
![]()
[/wpspoiler]
Με ποιο τρόπο μετατρέπουμε σε γινόμενο ένα τριώνυμο; Τι ρόλο παίζουν οι ρίζες του τριωνύμου σε αυτή τη διαδικασία;
ΑΛΓΕΒΡΑ Γ΄ ΓΥΜΝΑΣΙΟΥ

![]()
συνήθως την ονομάζουμε τριώνυμο και νομίζω ότι είναι προφανής ο λόγος αφού όπως βλέπουμε αποτελείται από τρεις μόνο όρους. Τον δευτεροβάθμιο όρο «αx2«, τον πρωτοβάθμιο όρο «βx» και από τον σταθερό όρο «γ». Για το τριώνυμο έχουμε ξαναμιλήσει σε προηγούμενο άρθρο κι έχουμε ασχοληθεί με το πως μπορούμε να βρούμε τις ρίζες του, θυμίζουμε ότι ρίζες του τριωνύμου είναι οι λύσεις της εξίσωσης
![]()
(αν θέλετε να το διαβάσετε αναλυτικά κάντε κλικ εδώ αν θέλετε να θυμηθείτε στα γρήγορα τη διαδικασία κάντε κλικ εδώ να δείτε τη μεθοδολογία).
Τώρα θα ασχοληθούμε με το πως μπορούμε να παραγοντοποιήσουμε ένα τριώνυμο δηλαδή με ποιο τρόπο μπορούμε να μετατρέψουμε ένα τριώνυμο σε γινόμενο. Για την παραγοντοποίηση γενικά έχουμε αναφερθεί προηγούμενα εδώ. Επειδή όμως στο σχολικό βιβλίο η παραγοντοποίηση του τριωνύμου παρουσιάζεται αρκετά αργότερα, δεν το είχαμε αναφέρει καθόλου τότε. Έφτασε λοιπόν η ώρα να ασχοληθούμε και με αυτό το θέμα.
Όταν λοιπόν για κάποιο λόγο χρειαστεί ένα τριώνυμο να το κάνουμε γινόμενο δεν έχουμε παρά να βρούμε τις ρίζες του έστω x1 και x2 και στη συνέχεια να χρησιμοποιήσουμε τον τύπο:
[su_note color=»#0972FB»]
[/su_note]![]()
Ας δούμε ένα παράδειγμα: Έστω ότι θέλουμε να μετατρέψουμε σε γινόμενο το ![]() .
.
Πρώτα απ’ όλα πρέπει να βρούμε τις ρίζες του και για το λόγο αυτό λύνουμε την εξίσωση
![]()
.
Έχουμε 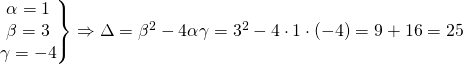
οπότε οι ρίζες είναι
![]()
![]()
Σύμφωνα με αυτά που αναφέραμε πιο πάνω παραγοντοποιούμε το τριώνυμο με τον τύπο και παίρνουμε
![]()
θα δούμε και δύο ακόμη παραδείγματα γιατί πιθανόν να δημιουργήθηκαν απορίες σε ορισμένους από εσάς για το τι κάνουμε στην περίπτωση που δεν έχουμε ρίζες ή στην περίπτωση που το τριώνυμο έχει διακρίνουσα ίση με μηδέν.
Αν ένα τριώνυμο όπως για παράδειγμα το x2+x+1 έχει διακρίνουσα αρνητική (Δ=-3) τότε όπως γνωρίζουμε δεν έχει ρίζες κι έτσι δεν μετατρέπεται σε γινόμενο.
Ενώ αν μας δωθεί για παραγοντοποίηση ένα τριώνυμο όπως το 4x2-12x+9 θα έχουμε
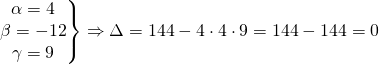
πράγμα που σημαίνει ότι έχουμε δύο ρίζες μόνο που στην περίπτωση αυτή θα είναι ίσες μεταξύ τους. Πράγματι
![]()
Έτσι χρησιμοποιώντας τον τύπο που δώσαμε παραπάνω παίρνουμε τελικά
![]()
το οποίο μάλλον θα ήταν πιο όμορφο αν το γράφαμε έτσι
![]()
![]()
![]()
![]()
![]()
Παρατηρούμε λοιπόν ότι ο τύπος για την παραγοντοποίηση τριωνύμου «δουλεύει» και όταν Δ>0 (δύο ρίζες διαφορετικές) αλλά και όταν Δ=0 (δύο ρίζες ίσες). Αν και όπως βλέπουμε κι από το προηγούμενο ακριβώς παράδειγμα το![]() μας δείχνει ότι το τριώνυμο ήταν ταυτότητα αλλά δεν το είχαμε προσέξει. Αυτό όμως είναι κανόνας που ισχύει πάντα «όταν η διακρίνουσα ενός τριωνύμου είναι ίση με μηδέν το τριώνυμο έχει δύο ρίζες ‘ισες χ1=χ2« κι επομένως θα ισχύει
μας δείχνει ότι το τριώνυμο ήταν ταυτότητα αλλά δεν το είχαμε προσέξει. Αυτό όμως είναι κανόνας που ισχύει πάντα «όταν η διακρίνουσα ενός τριωνύμου είναι ίση με μηδέν το τριώνυμο έχει δύο ρίζες ‘ισες χ1=χ2« κι επομένως θα ισχύει
![]()
Συνοψίζοντας λοιπόν όλα τα παραπάνω έχουμε:
[su_box title=»Μετατροπή τριωνύμου σε γινόμενο» color=»#0972FB»]
Το τριώνυμο ![]()
[su_list style=»arrow»]
όπου ![]() οι ρίζες του. [/su_list][/su_box]
οι ρίζες του. [/su_list][/su_box]
Για να λύσουμε εξισώσεις με απόλυτες τιμές (που ο άγνωστος είναι «φυλακισμένος» μέσα σε απόλυτα) πρέπει να ελευθερώσουμε τον άγνωστο από το απόλυτο. Πως μπορούμε να το πετύχουμε;
ΑΛΓΕΒΡΑ Α΄ ΛΥΚΕΙΟΥ
 Για το πως μπορούμε να απαλλαγούμε από τις απόλυτες τιμές που τυχόν εμφανίζονται σε μία αλγεβρική παράσταση έχουμε αναφερθεί σε προηγούμενο άρθρο μας (και καλό θα ήταν να του ρίξετε μια ματιά κάνοντας κλικ εδώ). Σε αυτή τη δημοσίευση θα ασχοληθούμε με εξισώσεις στις οποίες ο άγνωστος βρίσκεται πίσω από τις μπάρες της απόλυτης τιμής. Εξισώσεις δηλαδή που ο άγνωστος είναι «φυλακισμένος» μέσα σε μία ή και περισσότερες απόλυτες τιμές. Σκοπός μας σε μια τέτοια εξίσωση (όπως και σε κάθε εξίσωση άλλωστε) είναι να βρούμε ποιος αριθμός είναι «κρυμμένος πίσω από τη μάσκα του x». Στόχος μας είναι να «ελευθερώσουμε» το x μέσα από την απόλυτη τιμή. Για να το καταφέρουμε αυτό ας θυμηθούμε πρώτα τι είναι η απόλυτη τιμή ενός αριθμού και μετά βλέπουμε πως λύνουμε την εξίσωση.
Για το πως μπορούμε να απαλλαγούμε από τις απόλυτες τιμές που τυχόν εμφανίζονται σε μία αλγεβρική παράσταση έχουμε αναφερθεί σε προηγούμενο άρθρο μας (και καλό θα ήταν να του ρίξετε μια ματιά κάνοντας κλικ εδώ). Σε αυτή τη δημοσίευση θα ασχοληθούμε με εξισώσεις στις οποίες ο άγνωστος βρίσκεται πίσω από τις μπάρες της απόλυτης τιμής. Εξισώσεις δηλαδή που ο άγνωστος είναι «φυλακισμένος» μέσα σε μία ή και περισσότερες απόλυτες τιμές. Σκοπός μας σε μια τέτοια εξίσωση (όπως και σε κάθε εξίσωση άλλωστε) είναι να βρούμε ποιος αριθμός είναι «κρυμμένος πίσω από τη μάσκα του x». Στόχος μας είναι να «ελευθερώσουμε» το x μέσα από την απόλυτη τιμή. Για να το καταφέρουμε αυτό ας θυμηθούμε πρώτα τι είναι η απόλυτη τιμή ενός αριθμού και μετά βλέπουμε πως λύνουμε την εξίσωση.
Η απόλυτη τιμή ενός αριθμού ορίζεται και αλγεβρικά και γεωμετρικά. Εμείς θα αρκεστούμε στο δεύτερο μιας και είναι αρκετό για να στηριχτούμε σε αυτό και να καταφέρουμε να λύσουμε τις εξισώσεις.

Έτσι μπορούμε να εξηγήσουμε και πολλές από τις ιδιότητες της απόλυτης τιμής όπως
Η απόλυτη τιμή οποιουδήποτε αριθμού είναι είτε θετικός αριθμός είτε μηδέν, γιατί όπως είναι γνωστό αρνητική απόσταση δεν υπάρχει. Έτσι έχουμε,
Οι αντίθετοι αριθμοί έχουν την ίδια απόλυτη τιμή, αφού ισαπέχουν από το 0.
Σας θυμίζω ότι για να αντιλαμβανόμαστε καλύτερα τις εξισώσεις μπορούμε να τις θεωρούμε σαν ερωτήσεις. Έτσι η εξίσωση |x|= -5 , μας ρωτάει ποιος αριθμός είναι αυτός που απέχει από το 0 -5 μονάδες; Προφανώς η απάντηση είναι κανένας (αναφέραμε και πιο πάνω ότι δεν νοείται αρνητική απόσταση). Ενώ η απάντηση στην ερώτηση(=εξίσωση) |x|=0 είναι «ο μοναδικός αριθμός που απέχει από το μηδέν 0 μονάδες είναι ο 0». Όμως η εξίσωση |χ|=2 μας ζητάει να βρούμε τον αριθμό που απέχει από το 0 2 μονάδες. Η απάντηση είναι ότι δεν υπάρχει μόνο ένας αριθμός με αυτή την ιδιότητα αλλά δύο αριθμοί ο 2 και ο -2. Έτσι η εξίσωσή μας έχει δύο λύσεις τις x=2 ή x= -2. Για να γενικεύσουμε λίγο τα πράγματα και να τα βάλουμε σε μία τάξη δείτε το παρακάτω σχεδιάγραμμα.

Όπου βλέπετε f(x) θα εννοούμε «μια παράσταση που περιέχει x». Γιατί μέσα στο απόλυτο δεν είναι απαραίτητο να υπάρχει μόνο x, μπορεί κάποιοι «κακοί μαθηματικοί» (σαν κι εμένα) να ζητήσουν να λυθούν εξισώσεις που μέσα στο απόλυτο να υπάρχουν αρκετά πράγματα.
Για να λύσουμε οποιαδήποτε εξίσωση στην οποία το x βρίσκεται μέσα σε απόλυτο, πρέπει να στηριχτούμε στα συμπεράσματα του παραπάνω πίνακα. Πρέπει λοιπόν να απομονώσουμε το απόλυτο στο ένα μέλος και μετά κοιτώντας τι ρόλο παίζει το άλλο μέλος να αποφανθούμε αν η εξίσωση έχει λύσεις ή όχι και στην περίπτωση που έχει ποιες είναι αυτές. Ας δούμε τώρα μερικά παραδείγματα:
[gn_spoiler title=»Λύση:»]Φαίνεται η εξίσωση μας να έχει δύο διαφορετικές απόλυτες τιμές την |x| και την |-x|. Αυτό όμως δεν αληθεύει γιατί ξέρουμε ότι |-x|=|x|. Οπότε μπορούμε στην εξίσωση που μας δώσανε όπου έχει |-x| εμείς να βάλουμε |x|. Για να απομονώσουμε το απόλυτο που θέλουμε θα ακολουθήσουμε τη γνωστή διαδικασία που ακολουθούμε σε όλες τις εξισώσεις α΄ βαθμού.
Πρώτα θα διώξουμε τους παρονομαστές πολλαπλασιάζοντας κάθε όρο με το Ε.Κ.Π. των παρονομαστών που είναι το 12
![]()
![]()
Τώρα διώχνουμε τις παρενθέσεις κάνοντας χρήση της επιμεριστικής ιδιότητας
![]()
Χωρίζουμε τους γνωστούς από τους άγνωστους ώστε να μπορέσουμε να συνεχίσουμε τις πράξεις χωρίς να ξεχνάμε ότι προς το παρόν άγνωστος είναι το |x| κι όχι το x
![]()
![]()
άρα
![]()
ή πιο απλά
![]()
Αφού καταφέραμε κι απομονώσαμε το απόλυτο μπορούμε σύμφωνα με όσα έχουμε πει πιο πάνω ν΄απαντήσουμε ότι ![]() ή
ή ![]()
[/gn_spoiler]
[gn_spoiler title=»Λύση:»]Όπως θα παρατηρήσατε η εξίσωση αυτή είναι ίδια με την προηγούμενη με την μόνη αλλαγή αντί για |x| έχουμε |x-1|. Και πάλι επειδή οι αριθμοί 1-x και x-1 είναι αντίθετοι η εξίσωση θα γίνει
![]()
και θα λυθεί με τον ίδιο ακριβώς τρόπο καταλήγοντας στο
![Rendered by QuickLaTeX.com \[|x-1|=2 \Leftrightarrow\left\{\begin{matrix}x-1=-2\Leftrightarrow x=-2+1=-1\\ \eta\\x-1=2\Leftrightarrow x=2+1=3\end{matrix}\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-3d8b31a9400dddc58f39cee2363a52b1_l3.png)
Έτσι λοιπόν βλέπουμε ότι αν τα απόλυτα που έχουμε στην εξίσωση περιέχουν ίσες ή ακόμη και αντίθετες παραστάσεις, τότε δεν μας ενδιαφέρει το περιεχόμενη της απόλυτης τιμής. Λύνουμε την εξίσωση κανονικά όπως όλες τις εξισώσεις «κουβαλώντας» το απόλυτο μέχρι να καταφέρουμε να το απομονώσουμε και στο τέλος το πετάμε (πάντα σύμφωνα με το διάγραμμα που έχουμε παραπάνω).
Επειδή κάποιοι μπορεί να «ψιλό» μπερδεύονται κουβαλώντας το απόλυτο μπορούν να γλυτώσουν από αυτό με την συνηθισμένη στα μαθηματικά μέθοδο: «αν κάτι μ΄ενοχλεί κάνω πως δεν το βλέπω». Έτσι λοιπόν θα μπορούσαμε να θέσουμε όπου |x-1|=α (σχέση 1) και να λύσουμε την εξίσωση χωρίς το απόλυτο. Μόλις ξεμπερδέψουμε με το α και το βρούμε γυρίζουμε και το αντικαθιστούμε στη σχέση 1 απ’ όπου υπολογίζουμε το x που μας ενδιαφέρει.
Watch me 
Θέτω |χ-1|=α (σχέση 1) οπότε η εξίσωση γίνεται
![]()
![]()
![]()
![]()
![]()
Ας μην ξεχνάμε όμως ότι δεν ψάχναμε το α αλλά το x. Πάμε λοιπόν στη σχέση 1 και αντικαθιστούμε όπου α=2, οπότε
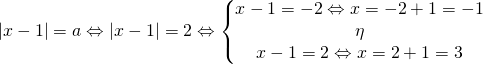
Τη μέθοδο αυτή για να είμαι ειλικρινής δεν σας την έδειξα μόνο για την περίπτωση που κάποιος δυσκολεύεται με τα πολλά απόλυτα αλλά και γιατί σε κάποιες περιπτώσεις θα έλεγα δεν μπορούμε να την αποφύγουμε γι’ αυτό καλό είναι να την ξέρουμε. Δείτε την επόμενη άσκηση και θα καταλάβετε. [/gn_spoiler]
[gn_spoiler title=»Λύση:»] Την άσκηση αυτή θα μπορούσαμε να τη λύσουμε απομονώνοντας το απόλυτο στο ένα μέλος, οπότε η εξίσωση να γίνει |x|=2 – x2 αλλά πιστεύω ότι έτσι δεν θα μας συνέφερε γιατί το δεύτερο μέλος (το 2 – x2) δεν γνωρίζουμε αν είναι θετικός ή αρνητικός αριθμός ( για κάποιες τιμές του x γίνεται θετικός, για κάποιες αρνητικός και για κάποιες γίνεται ίσος με 0). Έτσι θα έπρεπε να διακρίνουμε περιπτώσεις και να πούμε
Περίπτωση 1η: αν το 2 – x2 είναι αρνητικό η εξίσωσή μας είναι αδύνατη (βλέπε και το σχεδιάγραμμα πιο πάνω)
Περίπτωση 2η: αν ![]() , τότε x=2-x2 ή x= – (2-x2 ) και να λύσω δύο εξισώσεις (δεύτερου βαθμού η καθεμία) κι αφού βρω τις λύσεις να κρατήσω από αυτές μόνο εκείνες που επαληθεύουν τον περιορισμό
, τότε x=2-x2 ή x= – (2-x2 ) και να λύσω δύο εξισώσεις (δεύτερου βαθμού η καθεμία) κι αφού βρω τις λύσεις να κρατήσω από αυτές μόνο εκείνες που επαληθεύουν τον περιορισμό ![]() .
.
Για να γλυτώσουμε όλη αυτή τη δουλειά μπορούμε να σκεφτούμε λίγο πιο έξυπνα και να αντικαταστήσουμε το |x| με έναν άλλο αριθμό έστω α. Τότε θα έχουμε γλυτώσει και από το |x| αλλά και από το x2 γιατί το x2=|x2|=|x|2=α2 (ρίξε μια ματιά στις ιδιότητες των απολύτων). Ας δούμε τώρα πως έχει καταντήσει η εξίσωσή μας θέτοντας |x|=α,
![]()
Η διακρίνουσα του τριωνύμου είναι
![]()
και οι λύσεις της εξίσωσης αυτής είναι
![]()
ή
![]()
Εύκολα λοιπόν βρήκαμε το α, το x όμως είναι αυτό που μας ενδιαφέρει
![Rendered by QuickLaTeX.com \[\left | x \right |=\alpha \Leftrightarrow \left\{\begin{matrix} \left | x \right |=1 \Leftrightarrow x=\pm 1\\\eta'\\ \left | x \right |=-2 & \alpha \delta \upsilon \nu \alpha \tau \eta \end{matrix}\right.\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-198fbd64d110d48053f6e400aa566f03_l3.png)
[/gn_spoiler]
[gn_spoiler title=»Λύση:»] Στην άσκηση αυτή ανήκει στη γενική κατηγορία
![]()
και λύνεται με την ισοδυναμία
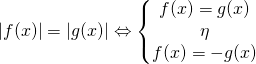
Έχουμε λοιπόν 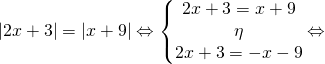
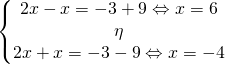 [/gn_spoiler]
[/gn_spoiler]
Ας δούμε ποια εξίσωση λέγεται κλασματική, πως βρίσκουμε τις λύσεις της και πως τους περιορισμούς. Δείτε πόσο σημαντικό είναι να μην ξεχνάμε να παίρνουμε περιορισμούς κάθε φορά που μια μεταβλητή εμφανίζεται σε παρονομαστή.
Κατ’ αρχάς ας δούμε τι εννοούμε όταν λέμε «κλασματικές εξισώσεις». Πολλοί μπορεί να θεωρούν ότι μια εξίσωση που έχει κλάσματα είναι μια κλασματική εξίσωση. Αυτό όμως δεν είναι σωστό γιατί μια εξίσωση τη λέμε κλασματική μόνο στη περίπτωση που υπάρχει άγνωστος σε ένα τουλάχιστον παρονομαστή της. Έτσι λοιπόν η εξίσωση ![]() ναι μεν έχει κλάσματα αλλά δεν είναι κλασματική αφού δεν υπάρχει άγνωστος σε κανένα παρονομαστή, ενώ η εξίσωση
ναι μεν έχει κλάσματα αλλά δεν είναι κλασματική αφού δεν υπάρχει άγνωστος σε κανένα παρονομαστή, ενώ η εξίσωση ![]() σύμφωνα με αυτά που προαναφέραμε είναι μια κλασματική εξίσωση αφού ο άγνωστος x «κυκλοφορεί» σε παρονομαστές. Δηλαδή ο x «δουλεύει υπογείως (ύπουλα)» πράγμα επικίνδυνο όπως θα δούμε παρακάτω.
σύμφωνα με αυτά που προαναφέραμε είναι μια κλασματική εξίσωση αφού ο άγνωστος x «κυκλοφορεί» σε παρονομαστές. Δηλαδή ο x «δουλεύει υπογείως (ύπουλα)» πράγμα επικίνδυνο όπως θα δούμε παρακάτω.
Στη συνέχεια θα επιλύσουμε μια κλασματική εξίσωση για να δούμε ποια μέθοδο ακολουθούμε και τι πρέπει να προσέξουμε.
Να βρείτε τις λύσεις της παρακάτω εξίσωσης ![]()
[wptabs mode=»horizontal»] [wptabtitle] Επίλυση[/wptabtitle] [wptabcontent]
|
Όπως σε όλες τις κατηγορίες εξισώσεων το πρώτο πράγμα που πρέπει να κάνουμε είναι να απαλλαγούμε από τους παρονομαστές (αν υπάρχουν) |
|
|
Για να το πετύχουμε αυτό πρέπει να παραγοντοποιήσουμε όσους από τους παρονομαστές παραγοντοποιούνται. Στην άσκησή μας ο μόνος που μπορεί να παραγοντοποιηθεί είναι ο |
|
|
Τώρα είμαστε σε θέση να βρούμε το Ε.Κ.Π., που είναι το γινόμενο όλων των παρονομαστών με την προϋπόθεση όμως κάθε παράγοντας να εμφανίζεται μία μόνο φορά και μάλιστα στη μεγαλύτερη δύναμη. Στο παράδειγμά μας το Ε.Κ.Π.=χ(χ+3). Πολλαπλασιάζουμε τώρα όλους τους όρους της εξίσωσης με το Ε.Κ.Π. |
|
|
Μετά από τις απλοποιήσεις έχουμε μια εξίσωση χωρίς παρονομαστές, όπως φαίνεται δίπλα. Σειρά τώρα για «αποχώρηση» έχουν οι παρενθέσεις ώστε να απελευθερώσουμε το x. Αυτό γίνεται με τη βοήθεια της επιμεριστικής ιδιότητας |
|
|
Συμμαζεύοντας λίγο (κάνουμε αναγωγή όμοιων όρων) θα προκύψει μια εξίσωση 1ου (οπότε χωρίζουμε γνωστούς – άγνωστους κτλ) ή 2ου βαθμού (τα μεταφέρουμε όλα στο ένα μέλος, υπολογίζουμε τη διακρίνουσα κτλ). Στην άσκηση που προσπαθούμε να λύσουμε τώρα παρότι δείχνει δεύτερου βαθμού (αφού έχει x2) αν τη δουλέψουμε λίγο θα δούμε ότι μετά την αναγωγή των όμοιων όρων θα προκύψει μια εξίσωση πρώτου βαθμού οπότε |
|
|
βρίσκουμε τελικά πως η εξίσωση που μας δόθηκε έχει λύση τον αριθμό -3. |
Μετά από αρκετό κόπο θα έλεγα φτάσαμε στο να βρούμε ότι η εξίσωση ![]() έχει λύση το x=-3.
έχει λύση το x=-3.

Κι όμως έχουμε κάνει ΜΕΓΑΛΟ ΛΑΘΟΣ κι αν έχεις κάνει το κόπο να φτάσεις μέχρι εδώ καλό θα ήταν να κάνεις κλικ στην καρτέλα «Περιορισμοί» για να δεις ποιο είναι το λάθος που κάναμε και πόσο σοβαρό είναι.
Επιστροφή^^^
[/wptabcontent]
[wptabtitle]Περιορισμοί[/wptabtitle] [wptabcontent]Όταν έχουμε να λύσουμε μια εξίσωση αναζητούμε ποια τιμή (ή ποιες τιμές) μπορεί να πάρει η άγνωστη μεταβλητή έτσι ώστε αν την αντικαταστήσουμε στην εξίσωση να προκύψει μια αληθής ισότητα (για παράδειγμα η λύση της εξίσωσης 2χ-8=0 είναι ο αριθμός 4 γιατί αν αντικαταστήσουμε το χ με τον αριθμό 4 θα προκύψει 2.4-8=0 που είναι μια σωστή πρόταση.
Στο προηγούμενο όμως άρθρο είχαμε αναφερθεί στους περιορισμούς (κάντε κλικ εδώ για να το δείτε). Εκεί λοιπόν είπαμε ότι δεν έχει νόημα στα μαθηματικά κλάσμα με παρονομαστή το 0. Γιαυτό όταν λύνουμε κλασματικές εξισώσεις θα πρέπει εκ των προτέρων να θέτουμε περιορισμούς για τον άγνωστο. Δηλαδή από την αρχή να δηλώνουμε ότι για τον άγνωστο, έστω χ, δεν μπορούμε να δεχτούμε κάποιες τιμές γιατί μηδενίζουν κάποιον από τους παρονομαστές της εξίσωσης.
Κατά την επίλυση μιας εξίσωσης σε όποια κατηγορία κι αν ανήκει αυτή (1ου ή 2ου βαθμού ή και κλασματική) σε κάθε μας βήμα (όταν διώχνουμε παρονομαστές, παρενθέσεις κτλ) δημιουργούμε μια άλλη εξίσωση πιο απλή από την αρχική που έχει ως λύσεις της τις λύσεις της προηγούμενης αλλά πιθανόν να έχει κι άλλες (περισσότερες). Στο τέλος τις επιπλέον λύσεις θα πρέπει να τις απορρίψουμε, να μην τις δεχτούμε δηλαδή ως λύσεις της αρχικής εξίσωσης. Αυτό ακριβώς έχει συμβεί και με την εξίσωση ![]() γιατί στην πορεία πήρε διάφορες μορφές μέχρι που κατέληξε να γίνει 4χ=-12. Εμείς βρήκαμε ότι χ=-3 αυτή όμως η λύση είναι η λύση της 4χ=-12 (γιατί αν βάλουμε όπου χ το -3 προκύπτει μια αληθής πρόταση η 4.(-3)=-12 και όχι της
γιατί στην πορεία πήρε διάφορες μορφές μέχρι που κατέληξε να γίνει 4χ=-12. Εμείς βρήκαμε ότι χ=-3 αυτή όμως η λύση είναι η λύση της 4χ=-12 (γιατί αν βάλουμε όπου χ το -3 προκύπτει μια αληθής πρόταση η 4.(-3)=-12 και όχι της ![]() γιατί εδώ δεν μπορούμε καν να βάλουμε όπου χ το -3 αφού θα μας μηδενίσει κάποιους παρονομαστές (τον χ2+3χ και τον χ+3).
γιατί εδώ δεν μπορούμε καν να βάλουμε όπου χ το -3 αφού θα μας μηδενίσει κάποιους παρονομαστές (τον χ2+3χ και τον χ+3).
Τι πρέπει να κάνουμε λοιπόν σε τέτοιες περιπτώσεις;
Πρέπει να παίρνουμε τα μέτρα μας, δηλαδή να παίρνουμε περιορισμούς.
ΚΑΘΕ ΠΑΡΟΝΟΜΑΣΤΗΣ ΠΡΕΠΕΙ ΝΑ ΜΗΝ ΓΙΝΕΤΑΙ ΙΣΟΣ ΜΕ 0
κι επειδή μέσα στο Ε.Κ.Π. είναι «κρυμμένοι» όλοι οι παρονομαστές της εξίσωσης είναι αρκετό να απαιτούμε
ΤΟ Ε.Κ.Π. ΝΑ ΜΗΝ ΓΙΝΕΤΑΙ ΠΟΤΕ ΙΣΟ ΜΕ 0 (![]() ).
).
Στη συγκεκριμένη επομένως άσκηση θα έπρεπε την ώρα που βρήκαμε το Ε.Κ.Π. να γράφαμε: ![]() πράγμα που σημαίνει ότι και το x αλλά και το x+3 πρέπει να είναι διάφορα του 0 δηλαδή με άλλα λόγια δεν μπορούμε να δεχτούμε σαν λύσεις ούτε το 0 αλλά ούτε και το -3. Πιο σύντομα και πιο «μαθηματικά» όλα τα παραπάνω θα μπορούσαν να γραφούν ως εξής:
πράγμα που σημαίνει ότι και το x αλλά και το x+3 πρέπει να είναι διάφορα του 0 δηλαδή με άλλα λόγια δεν μπορούμε να δεχτούμε σαν λύσεις ούτε το 0 αλλά ούτε και το -3. Πιο σύντομα και πιο «μαθηματικά» όλα τα παραπάνω θα μπορούσαν να γραφούν ως εξής:
![]()
![]()
![]()
Βλέπουμε λοιπόν ότι η εξίσωση που λύναμε τελικά δεν έχει λύση το -3 , άρα δεν έχει καμία λύση ήταν δηλαδή αδύνατη. Ξεχνώντας όμως τους περιορισμούς «την πατήσαμε». Επιστροφή^^^
[/wptabcontent]
[wptabtitle]Σε Έκτακτη Περίπτωση[/wptabtitle] [wptabcontent]Αν σε κάποια περίπτωση αδυνατούμε να βρούμε τους περιορισμούς είτε γιατί κάποιος δυσκολεύεται είτε γιατί δεν προλαβαίνει (π.χ. σε διαγώνισμα) τότε μπορεί να αποφύγει τα παραπάνω και απλώς να ελέγξει αν οι λύσεις που βρήκε μηδενίζουν το Ε.Κ.Π. και
αν το Ε.Κ.Π. μηδενίζεται, τότε η λύση απορρίπτεται αν όχι γίνεται δεκτή.
Στην άσκησή μας το Ε.Κ.Π. =![]() για x=-3 γίνεται Ε.Κ.Π.=-3.(-3+3)=-3.0=0 κι επομένως η λύση x=-3 απορρίπτεται.
για x=-3 γίνεται Ε.Κ.Π.=-3.(-3+3)=-3.0=0 κι επομένως η λύση x=-3 απορρίπτεται.
Μπορεί να σας κούρασα με την μεγάλη έκταση που είχε το άρθρο αλλά θεωρώ τις κλασματικές εξισώσεις λιγάκι δύσκολες για μαθητές Γ΄ Γυμνασίου αλλά και πολύ σημαντικές για τη συνέχεια. Αυτό που πρέπει να θυμόμαστε τελικά είναι πως οι κλασματικές εξισώσεις λύνονται όπως και όλες οι υπόλοιπες δηλαδή:
έτσι προκύπτει μια εξίσωση 1ου ή 2ου βαθμού που λύνουμε ανάλογα και
τέλος
ΔΕΝ ΞΕΧΝΑΜΕ ΝΑ ΕΛΕΓΞΟΥΜΕ ΑΝ ΟΙ ΛΥΣΕΙΣ ΠΟΥ ΒΡΗΚΑΜΕ ΠΕΡΝΟΥΝ ΤΟ (CRASH) TEST ΤΩΝ ΠΕΡΙΟΡΙΣΜΩΝ (δηλαδή να μην μηδενίζουν το Ε.Κ.Π.).
[/wptabcontent][/wptabs]
 Όταν μαθαίνουμε κάποιους καινούργιους ορισμούς στα μαθηματικά θα πρέπει να είμαστε πολύ προσεκτικοί, να προσέχουμε και την παραμικρή λεπτομέρεια. Έτσι ξεκινώντας από την πρώτη τάξη όπου μάθαμε τι είναι το κλάσμα (το
Όταν μαθαίνουμε κάποιους καινούργιους ορισμούς στα μαθηματικά θα πρέπει να είμαστε πολύ προσεκτικοί, να προσέχουμε και την παραμικρή λεπτομέρεια. Έτσι ξεκινώντας από την πρώτη τάξη όπου μάθαμε τι είναι το κλάσμα (το ![]() με
με ![]() λέγεται κλάσμα) στον ορισμό δηλώσαμε ότι ο παρονομαστής ενός κλάσματος δεν μπορεί να είναι ποτέ ίσος με το μηδέν. Δεν υπάρχει περίπτωση στην αριθμητική ποτέ να δούμε κάτι τέτοιο
λέγεται κλάσμα) στον ορισμό δηλώσαμε ότι ο παρονομαστής ενός κλάσματος δεν μπορεί να είναι ποτέ ίσος με το μηδέν. Δεν υπάρχει περίπτωση στην αριθμητική ποτέ να δούμε κάτι τέτοιο ![]() . Αριθμητική όμως κάναμε μόνο στο Δημοτικό, στο Γυμνάσιο και στο Λύκειο κάνουμε Άλγεβρα. Η βασική διαφορά που υπάρχει είναι ότι στην αριθμητική χρησιμοποιούμαι μόνο αριθμούς ενώ στην άλγεβρα χρησιμοποιούμε και γράμματα (τις μεταβλητές όπως λέγονται πιο σωστά). Έτσι λοιπόν από ‘δω και πέρα θα συναντήσουμε πάρα πολλές φορές κλάσματα που στον παρονομαστή τους θα περιέχουν και μεταβλητές, όπως αυτά
. Αριθμητική όμως κάναμε μόνο στο Δημοτικό, στο Γυμνάσιο και στο Λύκειο κάνουμε Άλγεβρα. Η βασική διαφορά που υπάρχει είναι ότι στην αριθμητική χρησιμοποιούμαι μόνο αριθμούς ενώ στην άλγεβρα χρησιμοποιούμε και γράμματα (τις μεταβλητές όπως λέγονται πιο σωστά). Έτσι λοιπόν από ‘δω και πέρα θα συναντήσουμε πάρα πολλές φορές κλάσματα που στον παρονομαστή τους θα περιέχουν και μεταβλητές, όπως αυτά ![]() ,
, ![]() ή
ή ![]() . Στις περιπτώσεις λοιπόν αυτές θα πρέπει να δηλώνουμε δίπλα από κάθε τέτοιο κλάσμα ότι ο παρονομαστής δεν μπορεί να γίνει μηδέν και για να διευκολύνουμε και αυτόν που πρόκειται να διαβάσει αυτό που γράψαμε είναι καλύτερο να γράφουμε ποια τιμή δεν επιτρέπεται να πάρει η μεταβλητή που βρίσκεται στον παρονομαστή που έχουμε. Τα κλάσματα επομένως που γράψαμε παραπάνω το σωστό θα ήταν να τα γράψουμε κάπως έτσι: Continue reading «Οι Περιορισμοί στα Μαθηματικά του Γυμνασίου»
. Στις περιπτώσεις λοιπόν αυτές θα πρέπει να δηλώνουμε δίπλα από κάθε τέτοιο κλάσμα ότι ο παρονομαστής δεν μπορεί να γίνει μηδέν και για να διευκολύνουμε και αυτόν που πρόκειται να διαβάσει αυτό που γράψαμε είναι καλύτερο να γράφουμε ποια τιμή δεν επιτρέπεται να πάρει η μεταβλητή που βρίσκεται στον παρονομαστή που έχουμε. Τα κλάσματα επομένως που γράψαμε παραπάνω το σωστό θα ήταν να τα γράψουμε κάπως έτσι: Continue reading «Οι Περιορισμοί στα Μαθηματικά του Γυμνασίου»