Μήνας: Νοεμβρίου 2010

Πράξεις με μιγαδικούς

Αφού γνωρίσαμε το σύνολο των μιγαδικών αριθμών ήρθε ο καιρός να δούμε και πως μπορούμε να κάνουμε πράξεις μέσα σε αυτό το σύνολο. Πριν ξεκινήσουμε όμως καλό θα ήταν να αναφερθούμε και στη ισότητα των μιγαδικών. Έστω λοιπόν ότι έχουμε δύο μιγαδικούς, τον z1=x1+y1i και τον z2=x2+y2i, τότε

Ισότητα μιγαδικών

Δύο μιγαδικοί z_1=x_1+y_1i , z_2=x_2+y_2i θα λέμε ότι είναι ίσοι αν έχουν ίσα πραγματικά αλλά και φανταστικά μέρη. Δηλαδή,z_1=z_2\Leftrightarrow\left\{\begin{matrix} x_1=x_2\\ \kappa \alpha \iota \\ y_1=y_2 \end{matrix}

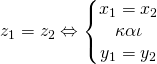
Από εδώ προκύπτει και το πότε ένας μιγαδικός θα είναι ίσος με 0. Πράγματι ένας μιγαδικός z=x+yi θα είναι ίσος με μηδέν (0=0+0i) αν και μόνο αν ισχύει x=0 και y=0.

Πρόσθεση κι αφαίρεση:

Πρόσθεση Μιγαδικών

Για να προσθέσουμε (ή να αφαιρέσουμε) μιγαδικούς προσθέτουμε (ή αφαιρούμε) τα πραγματικά τους μέρη και το ίδιο κάνουμε με

τα φανταστικά τους μέρη. Δηλαδή,z_1+z_2=(x_1+y_1i)+(x_2+y_2i)=(x_1+x_2)+(y_1+y_2)i z_1-z_2=(x_1+y_1i)-(x_2+y_2i)=(x_1-x_2)+(y_1-y_2)i

Παράδειγμα: (3+12i)+(5-4i)=(3+5)+(12-4)i=8+8i

Πολλαπλασιασμός μιγαδικών:

Γιά να πολλαπλασιάσουμε τους μιγαδικούς z1 και z2 κάνουμε χρήση της γνωστής μας επιμεριστικής ιδιότητας κι έτσι έχουμε,

    \[z_1\cdot z_2=(x_1+y_1i)(x_2+y_2i)=x_1x_2+x_1y_2i+y_1x_2i+y_1y_2i^2=\]

    \[(x_1x_2-y_1y_2)+(x_1y_2+x_2y_1)i\]

(θυμηθείτε ότι i2=-1)

Αν ο z1 είναι πραγματικός, δηλαδή z1=λ, τότε λz2=λ(x2+y2i)=λx2+λy2i.

Παράδειγμα: (1-2i)(3-4i)=3-4i-6i+8i2=3-8-4i-6i=-5-10i

Μέχρι εδώ όλα καλά κι εύκολα το μόνο που μας έμεινε ακόμη είναι να δούμε πως διαιρούμε μιγαδικούς αριθμούς. Πριν όμως αναφερθούμε στη διαίρεση θα χρειαστεί να ορίσουμε τον «συζυγή» ενός μιγαδικού. Κάτι αντίστοιχο είχαμε κάνει και για να ορίσουμε την πράξη της διαίρεσης στους ρητούς αριθμούς. Πρώτα είδαμε τι ονομάζεται αντίστροφος ενός αριθμού και μετά είπαμε ότι γιά να διαιρέσουμε δύο ρητούς πολλαπλασιάζουμε τον διαιρετέο με τον αντίστροφο του διαιρέτη. Κάτι ανάλογο κάνουμε κι εδώ.

Συζυγής ενός μιγαδικού:Συζυγείς Μιγαδικοί

Αν θεωρήσουμε το μιγαδικό z=x+yi, ονομάζουμε συζυγή του z και τον συμβολίζουμε με \bar{z} τον μιγαδικό x-yi. Δηλαδή 

    \[z=x+yi\Leftrightarrow\bar{z}=x-yi\]

Προφανώς ισχύουν και τα παρακάτω:

Ο z είναι πραγματικός αν και μόνο αν 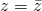z=\bar{z} και ο z είναι φανταστικός αν και μόνο αν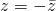 z=-\bar{z}

Την απόδειξη των παραπάνω καθώς και άλλες σχέσεις που αφορούν στο συζυγή ενός μιγαδικού θα δούμε σε επόμενο άρθρο για να μη βγούμε τώρα εκτός θέματος. Αυτό που θα χρειαστούμε όμως για τη διαίρεση, που σκοπεύουμε να καταλήξουμε, είναι η σχέση:

αν z=x+yi, τότε ισχύει:

    \[z \bar{z}=x^2+y^2\]

Πράγματι,

    \[z \bar{z}=(x+yi)(x-yi)=x^2-y^2i^2=x^2+y^2\]

Τώρα νομίζω είμαστε έτοιμοι να ορίσουμε και τη διαίρεση

Διαίρεση μιγαδικών:

Γιά να βρούμε το πηλίκο  δύο μιγαδικών z1 και z2, πολλαπλασιάζουμε και διαιρούμε με τον συζυγή του παρονομαστή. Δηλαδή,

    \[\frac{z_1}{z_2}=\frac{z_1 \bar{z_2}}{z_2 \bar{z_2}}=\frac{z_1 \bar{z_2}}{x_2^2+y_2^2}\]

Παράδειγμα: \frac{1-2i}{3+4i}=\frac{(1-2i)(3-4i)}{(3+4i)(3-4i)}=\frac{3-4i-6i+8i^2}{3^2+4^2}= \frac{-5-10i}{25}=-\frac{5}{25}-\frac{10}{25}i=-\frac{1}5-\frac{2}5i