4 σκέψεις σχετικά με το “Εξισώσεις & Ανισώσεις 1ου Βαθμού – Βιντεομάθημα”
Ευχαριστώ πολύ! Πολύ βοηθητικό βίντεο!!Μπορεί κάποιος να με βοηθήσει να λύσω μία άσκηση; Είναι πολλή εύκολη αλλά δεν ξέρω τι πρέπει να κάνω πρώτα: να λύσω κάθε ανίσωση χωριστά και να βρω τις κοινές λύσεις με τη βοήθεια του άξονα των πραγματικών αριθμών ή κάτι άλλο;
1) Να βρεθούν οι τιμές του χ για τις οποίες συναληθεύουν οι ανισώσεις, να παραστήσετε τις λύσεις τους στον άξονα των αριθμών και να τις συμβολίσετε με τη μορφή διαστήματος:
α) και
β)
γ) και
δ)
Ευχαριστώ!!!!
Θανάση, συνήθως δεν κάνουμε τίποτα παραπάνω, γιατί συνήθως αυτό που ζητάει η άσκηση είναι να βρεθούν οι κοινές λύσεις δύο ή και περισσότερων ανισώσεων. Αυτά που διάβασες αφορούν μαθητές κυρίως Β΄ Γυμνασίου, αργότερα σε μεγαλύτερες τάξεις θα χρειαστεί και κάτι παραπάνω όπως για παραδειγμα όταν ψάχνουμε το πεδίο ορισμού μιας συνάρτησης. Αν είσαι σε μεγαλύτερη τάξη και θες κάτι παραπάνω πες μου να «εμβαθύνω» περισσότερο.
Ευχαριστώ πολύ! Πολύ βοηθητικό βίντεο!!Μπορεί κάποιος να με βοηθήσει να λύσω μία άσκηση; Είναι πολλή εύκολη αλλά δεν ξέρω τι πρέπει να κάνω πρώτα: να λύσω κάθε ανίσωση χωριστά και να βρω τις κοινές λύσεις με τη βοήθεια του άξονα των πραγματικών αριθμών ή κάτι άλλο; και
και 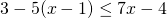
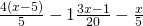
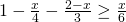 και
και 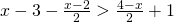
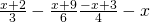
1) Να βρεθούν οι τιμές του χ για τις οποίες συναληθεύουν οι ανισώσεις, να παραστήσετε τις λύσεις τους στον άξονα των αριθμών και να τις συμβολίσετε με τη μορφή διαστήματος:
α)
β)
γ)
δ)
Ευχαριστώ!!!!
Ακριβώς Λίζα όπως τα λες Πρέπει να λύσεις κάθε ανίσωση χωριστά και με τη βοήθεια του άξονα των πραγματικών αριθμών να βρεις τις κοινές λύσεις.
π.χ.
προφανώς εδώ δεν υπάρχουν κοινές λύσεις
καλησπερα,
Βρισκουμε τις κοινες λυσεις…μετα που τις χρησημοποιυμε δεν καταλαβα…?
ευχαριστω.
Θανάση, συνήθως δεν κάνουμε τίποτα παραπάνω, γιατί συνήθως αυτό που ζητάει η άσκηση είναι να βρεθούν οι κοινές λύσεις δύο ή και περισσότερων ανισώσεων. Αυτά που διάβασες αφορούν μαθητές κυρίως Β΄ Γυμνασίου, αργότερα σε μεγαλύτερες τάξεις θα χρειαστεί και κάτι παραπάνω όπως για παραδειγμα όταν ψάχνουμε το πεδίο ορισμού μιας συνάρτησης. Αν είσαι σε μεγαλύτερη τάξη και θες κάτι παραπάνω πες μου να «εμβαθύνω» περισσότερο.