Επίλυση της τριγωνομετρικής εξίσωσης ημχ=α

Έχουμε δει σε προηγούμενο άρθρο ότι εξίσωση είναι μια ισότητα που περιέχει τουλάχιστον έναν άγνωστο. Αν όμως ο άγνωστος είναι «φυλακισμένος» μέσα σε κάποιο τριγωνομετρικό αριθμό (ημίτονο, συνημίτονο, εφαπτομένη ή συνεφαπτομένη) τότε έχουμε μια ειδική κατηγορία εξισώσεων που λέγονται τριγωνομετρικές εξισώσεις. Παράδειγμα η εξίσωση $2\sigma\upsilon\nu(x)=-1$ και η $\epsilon\phi(2x+\frac{\pi}{3})=1$ είναι τριγωνομετρικές εξισώσεις αφού το x είναι κλεισμένο μέσα σε τριγωνομετρικό αριθμό, ενώ η εξίσωση $2\epsilon\phi(\frac{\pi}4)=x+1$ δεν είναι γιατί παρότι υπάρχει ενας τριγωνομετρικός αριθμός, ο άγνωστος x κυκλοφορεί ελύθερος.

Παράδειγμα

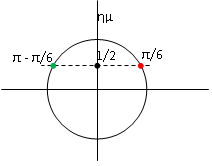
Μια τριγωνομετρική εξίσωση όπως η $\eta\mu\chi=\frac{1}2$ μας ρωτάει: «ποια γωνία έχει ημίτονο ίσο με 1/2;» Η πρώτη γωνία που μας έρχεται στο μυαλό είναι η π/6 (=30^ο). Είναι όμως η μοναδική γωνία που έχει ημίτονο ισο με 1/2; Η απάντηση αν το σκεφτούμε λίγο είναι προφανώς όχι αφού εκτός από τη γωνία π/6 και η γωνία π-π/6 (=5π/6=150^ο) ,που είναι η παραπληρωματική της π/6, έχει ημίτονο ίσο με 1/2. Θυμηθείτε ότι οι παραπληρωματικές γωνίες έχουν ίδιο ημίτονο ( το μάθαμε στο Γυμνάσιο ) πράγμα που φαίνεται από τον τριγωνομετρικό κύκλο (ρίξτε μια ματιά στην εικόνα) αλλά και από τη γραφική παράσταση του ημιτόνου. Αλλά κι όλες οι γωνίες που (ανεξαρτήτως πόσες στροφές έχουμε κάνει στον τριγωνομετρικό κύκλο) καταλήγουν στο π/6 ή στο π-π/6, έχουν κι αυτές ημίτονο ίσο με 1/2.

Δηλαδή

	0 στροφές+π/6	1 στροφή+π/6	2 στροφές+π/6	3 στροφές+π/6	k στροφές +π/6
χ	π/6	2π+π/6	2(2π)+π/6	3(2π)+π/6	k(2π)+π/6
ημχ	1/2	1/2	1/2	1/2	1/2

	0 στροφές+(π-π/6)	1 στροφή+(π-π/6)	2 στροφές+(π-π/6)	3 στροφές+(π-π/6)	k στροφές +(π-π/6)
χ	(π-π/6)	2π+(π-π/6)	2(2π)+(π-π/6)	3(2π)+(π-π/6)	k(2π)+(π-π/6)
ημχ	1/2	1/2	1/2	1/2	1/2

Βλέπουμε λοιπόν ότι υπάρχουν άπειρες γωνίες με ημίτονο 1/2, χωρισμένες σε δύο ομάδες, αυτές που καταλήγουν στο π/6 και αυτές που καταλήγουν στο (π-π/6), ‘ετσι αν θέλαμε να τις γράψουμε όλες αναλυτικά δεν θα μπορούσαμε. Μπορούμε όμως να τις περιγράψουμε και να πούμε ότι: χ=2kπ+π/6 ή χ=2kπ+(π-π/6), όπου το k είναι ακέραιος αριθμός (στην πραγματικότητα το k είναι «μετρητής στροφών» ,

για k=0 παίρνουμε τις γωνίες π/6 και π-π/6=5π/6,

για k=1 εχουμε κάνει μια στροφή και έχουμε καταλήξει στα σημεία π/6 και π-π/6 άρα έχουμε τις γωνίες 2π+π/6 και 2π+(π-π/6)=2π+5π/6 κ.ο.κ. δηλαδή

	k=-2	k=-1	k=0	k=1	k=2
χ	-4π+π/6	-2π+π/6	π/6	2π+π/6	4π+π/6
χ	-4π+5π/6	-2π+5π/6	5π/6	2π+5π/6	4π+5π/6

Γενίκευση

Μην ξεχνάτε ότι μέχρι εδώ ασχοληθήκαμε μόνο με ένα παράδειγμα, δηλαδή λύναμε την τριγωνομετρική εξίσωση $\eta\mu\chi=1/2$ . Τώρα ήρθε η ώρα να το γενικεύσουμε λίγο: Αν είχαμε να λύσουμε μια εξίσωση της μορφής

$\eta\mu\chi=\alpha$

θα έπρεπε να βρούμε μια γωνία από τον πρώτο κύκλο που να ικανοποιούσε αυτή την ισότητα (μια αρχική λύση ας πούμε), δηλαδή να βρούμε μια γωνία που να έχει ημίτονο ίσο με α. Έστω ότι την βρήκαμε κι η γωνία αυτή είναι η θ (πρέπει δηλαδή να ισχύει ημθ=α), τότε

οι λύσεις της
$\eta\mu\chi=\alpha\Leftrightarrow\eta\mu\chi=\eta\mu\theta$

θα είναι
$\chi=2k\pi+\theta , \chi=2k\pi+(\pi-\theta)$

Κάντε κλικ να δείτε και τις υπόλοιπες τριγωνομετρικές εξισώσεις καθώς και λυμένες ασκήσεις .

Παράδειγμα

Γενίκευση

Αφήστε μια απάντηση Ακύρωση απάντησης