Μιγαδικοί με το μέτρο

Μέτρο Μιγαδικού Αριθμού — Το μέτρο ενός μιγαδικού είναι η απόστασή του μιγαδικού από την αρχή των αξόνων

Γ΄ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗ

Εισαγωγή – Ορισμός

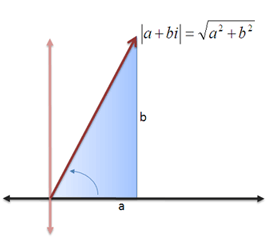
Σε προηγούμενο άρθρο, που κάναμε την εισαγωγή στους μιγαδικούς αριθμούς, είδαμε ότι ένας μιγαδικός αριθμός μπορεί να παρασταθεί στο μιγαδικό επίπεδο και σαν ένα διάνυσμα (μπορείτε να ρίξετε μια ματιά εδώ να το θυμηθείτε). Αυτό μας δίνει το «δικαίωμα» να ορίσουμε και το μέτρο ενός μιγαδικού ακριβώς όπως είχαμε ορίσει το μέτρο ενός διανύσματος στη Β΄Λυκείου. Δηλαδή, το μέτρο ενός μιγαδικού $z=a+bi$ είναι το μήκος του διανύσματος $\overrightarrow{OM}$ όπου Ο η αρχή των αξόνων και Μ το σημείο με συντεταγμένες Μ(a,b). Έτσι λοιπόν μπορούμε εύκολα με το Πυθαγόρειο θεώρημα να καταλήξουμε στο:

αν $z=a+bi$ , τότε το μέτρο του z (συμβολίζεται $|z|$ ) και είναι ίσο με
$\left| z \right|=\left| a+bi\right|=\sqrt{a^2+b^2}$

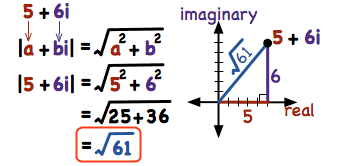
Παρατηρήσεις

Το μέτρο ενός μιγαδικού δεν είναι μιγαδικός αλλά πραγματικός αριθμός και μάλιστα μη αρνητικός, δηλαδή
$\left | z \right |\geq0$
Στην περίπτωση που ο z είναι πραγματικός η έννοια του μέτρου ταυτίζεται με την έννοια της απόλυτης τιμής.
Το μέτρο ενός μιγαδικού είναι ίσο με το μέτρο του συζυγούς του (δείτε εδώ τι είναι ο συζυγής) και αυτό γιατί αν z=a+bi, τότε ισχύει $\left | \overline{z} \right |=\left|a-bi\right|=\sqrt{a^2+\left(-b\right)^2}=\sqrt{a^2+b^2}=\left|z\right|$ άρα $\left|\overline{z}\right|=\left|z\right|$
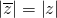
Συνήθως στις ασκήσεις για να «γλιτώνουμε την ταλαιπωρία» της τετραγωνικής ρίζας αντί για το μέτρο του z υπολογίζουμε το |z|²=a²+b² και μάλιστα ισχύει:
$\left|z\right|^2=z \cdot \overline{z}$

και αυτό γιατί
$z\cdot \overline{z}=(a+bi)(a-bi)=a^2-b^2i^2=a^2+b^2=|z|^2$

(θυμίζουμε i²=-1)
To μέτρο της διαφοράς δύο μιγαδικών είναι ίσο με την απόσταση των εικόνων τους. Δηλαδή η παράσταση |z-w| γεωμετρικά δηλώνει την απόσταση των μιγαδικών z και w στο μιγαδικό επίπεδο.

Ας δούμε τώρα όλες τις ιδιότητες του μέτρου

Ιδιότητες

αν z=a+bi και w=x+yi, τότε

ComplexGraph — το μέτρο του z είναι ίσο με το μέτρο του συζυγούς του

$|z|=\sqrt{a^2+b^2}\geq0$

$|\overline{z}|=|z|=|-z|=|-\overline{z}|$

$|z|^2=z \cdot \overline{z}$

$|z \cdot w|=|z| \cdot |w|$

$\left|\frac{z}{w}\right|=\frac{ \left|z\right|}{ \left|w\right|}$

$|z^{\nu}|=|z|^{\nu}$

Αυτά τα λίγα είχαμε να πούμε για το μέτρο του μιγαδικού θα ακολουθήσει άρθρο με λυμένα παραδείγματα (update: κάντε κλικ εδώ να δείτε τα λυμένα παραδείγματα) ώστε να μάθουμε να χρησιμοποιούμαι τις παραπάνω ιδιότητες καθώς και ένα ακόμη με την πολύ σημαντική ενότητα των γεωμετρικών τόπων. Γι’ αυτό μείνετε «συντονισμένοι».

Εισαγωγή – Ορισμός

Παρατηρήσεις

Ιδιότητες

Αφήστε μια απάντηση Ακύρωση απάντησης