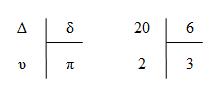Ευκλείδεια Διαίρεση

Όταν μας δοθούν δύο φυσικοί αριθμοί έστω Δ και δ, τότε υπάρχουν δύο άλλοι φυσικοί αριθμοί π και υ, έτσι ώστε να ισχύει η ισότητα (που ονομάζεται Ταυτότητα της Ευκλείδειας Διαίρεσης ):

$\Delta = \delta \cdot \pi + \upsilon$ , με υ<δ

Ο αριθμός Δ λέγεται διαιρετέος
Ο αριθμός δ λέγεται διαιρέτης
Ο αριθμός π λέγεται πηλίκο και
Ο αριθμός υ λέγεται υπόλοιπο
Όπως είναι γνωστό ο διαιρέτης δεν μπορεί να είναι το 0.

Παράδειγμα: κάνοντας τη διαίρεση του 15 με το 2, έχουμε:

Η ταυτότητα της διαίρεσης σε αυτή τη περίπτωση είναι: $15=2 \cdot 7+1$ , όπου Δ=15, δ=2, π=7 και υ=1

• Κάθε ισότητα της μορφής $\Delta = \delta \cdot \pi + \upsilon$ δεν παριστάνει υποχρεωτικά διαίρεση. Πρέπει πάντα να ισχύει και υ<δ .
Έτσι η ισότητα $27=4 \cdot 6+3$ παριστάνει τη διαίρεση του 27 με το 4 ή του 27 με το 6.
Η ισότητα $27=3 \cdot 8+3$ , παριστάνει τη διαίρεση του 27 με το 8 και όχι του 27 με το 3 γιατί το υ=3 δεν είναι μικρότερο του δ=3.
Όπως και η ισότητα $27=2 \cdot 5+17$ δεν μπορεί να είναι ταυτότητα διαίρεσης αφού 17>2 και 17>5.
Όταν το υπόλοιπο της διαίρεσης του Δ με τον δ είναι ίσο με μηδέν, τότε η διαίρεση λέγεται τέλεια και ισχύει η ισότητα: $\Delta = \delta \cdot \pi$ .
• Στη περίπτωση της τέλειας διαίρεσης του Δ με τον δ μπορούμε να χρησιμοποιούμε και τις παρακάτω ισοδύναμες εκφράσεις:
i. Ο δ διαιρεί τον Δ
ii. Ο δ είναι διαιρέτης του Δ
iii. Ο Δ διαιρείται από τον δ
iv. Ο Δ είναι πολλαπλάσιο του δ.

Αφήστε μια απάντηση Ακύρωση απάντησης