Όρια – mathland

ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ΄ ΛΥΚΕΙΟΥ

Σε προηγούμενο άρθρο μας, είδαμε πως μπορούμε να υπολογίσουμε το όριο μιας συνάρτησης f για την οποία δεν μας έχουν δώσει τον τύπο της αλλά μας έχουν δώσει ένα όριο μιας άλλης συνάρτησης, έστω g, στον τύπο της οποίας εμφανίζεται και η f. Στο συγκεκριμένο άρθρο είδαμε πως έχουμε τη δυνατότητα να φτιάξουμε εμείς έναν τύπο για τη συνάρτηση f ( λύνοντας τον τύπο της g ως προς f ) και στη συνέχεια να υπολογίσουμε κατά τα γνωστά το όριο της f.

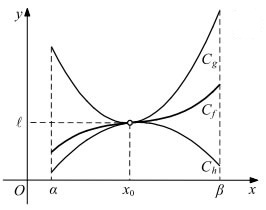
paremvoli — Κριτήριο Παρεμβολής ή Sandwich Theorem

Σήμερα θα συνεχίσουμε τη «υπόθεση» αυτή για να δούμε τι μπορούμε να κάνουμε στην περίπτωση που και πάλι δεν γνωρίζουμε τον τύπο της συνάρτησης f αλλά ούτε και κάποιο όριο στο οποίο να συμμετέχει αυτή. Σύμφωνα με αυτά που υπάρχουν στην ύλη μας αυτό που θα πρέπει οπωσδήποτε να έχουμε για να βρούμε το όριο είναι μια «διπλή ανισότητα» στο κέντρο της οποίας να βρίσκεται η συνάρτηση f και στα άκρα αυτής δύο συναρτήσεις, έστω g και h, οι οποίες να έχουν το ίδιο όριο όταν το x τείνει στο x₀. Δηλαδή να έχουμε κάτι τέτοιο:

$g(x) \le f(x) \le h(x)$ που να ισχύει για κάθε x που περιέχεται σε μια περιοχή του x₀

κι επιπλέον να ισχύει: $\underset{x \to x_0}{\mathop{\lim}}g(x)=\underset{x \to x_0}{\mathop{\lim}}h(x)=l$

τότε και η συνάρτηση f θα συγκλίνει σε ένα αριθμό ο οποίος υποχρεούται να βρίσκεται ανάμεσα στο l και στο l και προφανώς δεν μπορεί να είναι άλλος από τον l. Έτσι λοιπόν θα ισχύει $\underset{x \to x_0}{\mathop{\lim}}f(x)=l$ .

Αυτό που είδαμε παραπάνω, δηλαδή αν η f είναι «φραγμένη» από πάνω και από κάτω από δύο συναρτήσεις που έχουν το ίδιο όριο στο x₀ τότε και αυτή θα έχει το ίδιο όριο όταν το x τείνει στο x₀ είναι το λεγόμενο «Κριτήριο Παρεμβολής»

Έστω οι συναρτήσεις g,f,h για τις οποίες ισχύουν:
(α) $g(x) \le f(x) \le h(x)$ για κάθε x που βρίσκεται κοντά στο x₀ και

(β) $\underset{x \to x_0}{\mathop{\lim}}g(x)=\underset{x \to x_0}{\mathop{\lim}}h(x)=l$

τότε θα ισχύει, $\underset{x \to x_0}{\mathop{\lim}}f(x)=l$

Ας δούμε ένα απλό παράδειγμα για να καταλάβουμε πότε και πως χρησιμοποιούμε το κριτήριο παρεμβολής και στη συνέχεια διαβάστε τις λυμένες ασκήσεις που βρίσκονται παρακάτω όπου θα δούμε τι γίνεται όταν η συνάρτηση της οποίας θέλω να βρω το όριο δεν βρίσκεται στο κέντρο της διπλής ανισότητας ή ακόμη χειρότερα τι κάνουμε όταν δεν μας έχουν δώσει καθόλου αυτή τη διπλή ανισότητα.

Παράδειγμα:

Η συνάρτηση f είναι ορισμένη στο $\mathbb{R}$ και για κάθε $x \in \mathbb{R}$ ισχύει η σχέση: $-x^2+2x \le f(x) \le x^2 +2x$ . Να βρεθεί το όριο της f στο 0.

Λύση:

Έστω $g(x)=-x^2+2x$ , τότε $\underset{x \to 0}{\mathop{\lim}}g(x)=0$ και

$h(x)=x^2+2x$ , για την οποία ισχύει $\underset{x \to 0}{\mathop{\lim}}h(x)=0$ . Από το κριτήριο παρεμβολής ισχύει ότι $\underset{x \to 0}{\mathop{\lim}}f(x)=0$

[wptabs mode=»horizontal»][wptabtitle]Άσκηση 1[/wptabtitle] [wptabcontent]Η συνάρτηση f είναι ορισμένη στο $\mathbb{R}$ και για κάθε $x \in \mathbb{R}$ ισχύει η σχέση: $|f(x)-1|<|x^2+x|$ . Να βρεθεί το όριο της f στο 0.

Λύση:

Στην άσκηση αυτή το πρώτο πρόβλημα που έχουμε είναι ότι δεν μας έχουν δώσει μια διπλή ανισότητα. Αυτο όμως ξεπερνιέται πολύ εύκολα αρκεί να θυμηθούμε μια ιδιότητα των απολύτων τιμών: $|x| \le \theta \Leftrightarrow - \theta \le x \le \theta$ οπότε η σχέση που μας δώσανε θα πάρει τη μορφή $-|x^2+x| \le f(x)-1 \le |x^2+x|$ και να τη η διπλή ανισότητα!

Το δεύτερο πρόβλημα που έχουμε εδώ είναι ότι η συνάρτηση f που μας ενδιαφέρει δεν είναι μόνη της στο κέντρο της ανισότητας αυτής, υπάρχει μαζί της και το -1. Κι αυτό όμως το πρόβλημα λύνεται εύκολα προσθέτοντας σε κάθε μέλος της ανισότητας το +1. Έτσι παίρνουμε

$-|x^2+x| \le f(x)-1 \le |x^2+x| \Leftrightarrow$

$-|x^2+x|+1 \le f(x)-1+1 \le |x^2+x|+1 \Leftrightarrow$

$-|x^2+x|+1 \le f(x) \le |x^2+x|+1$

Τώρα είμαστε έτοιμοι να εφαρμόσουμε το κριτήριο παρεμβολής κι έχουμε, $g(x)=-|x^2+x|+1$ , $h(x)=|x^2+x|+1$ επίσης $\underset{x \to 0}{\mathop{\lim}}g(x)= \underset{x \to 0}{\mathop{\lim}}h(x)=1$ οπότε συμπεραίνουμε ότι $\underset{x \to 0}{\mathop{\lim}}f(x)=1$ .
Δείτε και την άσκηση 2 ^^^[/wptabcontent]

[wptabtitle]Άσκηση 2[/wptabtitle] [wptabcontent]Δίνεται η συνάρτηση $f:\mathbb{R}\rightarrow\mathbb{R}$ για την οποία ισχύει: $|f(x)-2| \le x^2$ για κάθε $x \in \mathbb{R}$ . Να βρείτε τα παρακάτω όρια

(α) $\underset{x \to 0}{\mathop{\lim}}f(x)$ και

(β) $\underset{x \to 0}{\mathop{\lim}}\frac{f(x)-\sqrt{x+4}}{x}$

Λύση:

(α) Όπως και στην προηγούμενη άσκηση πρώτα φτιάχνω τη διπλή ανισότητα:

$|f(x)-2| \le x^2\Leftrightarrow$

$-x^2 \le f(x)-2 \le x^2 \Leftrightarrow$

τώρα απομονώνω την f στο κέντρο της ανισότητας:

$2-x^2 \le f(x) \le 2+x^2$

κι επειδή $\underset{x \to 0}{\mathop{\lim}}(2-x^2)=\underset{x \to 0}{\mathop{\lim}}(2+x^2)=2$ θα ισχύει και $\underset{x \to 0}{\mathop{\lim}}f(x)=2$ .

(β) Έστω $g(x) =\frac{f(x)-\sqrt{x+4}}{x}$ κι αναζητώ το όριο της g στο 0. Παρατηρώ ότι αν χρησιμοποιήσω αυτό που βρήκα στο (α) ερώτημα (ότι $\underset{x \to 0}{\mathop{\lim}}f(x)=2$ ) καταλήγω σε απροσδιόριστη μορφή 0/0. Έτσι λοιπόν αναγκάζομαι να περάσω την g στο κέντρο της διπλής ανισότητας ως εξής:

$2-x^2 \le f(x) \le 2+x^2\Leftrightarrow$

$2-x^2-\sqrt{x+4} \le f(x)-\sqrt{x+4} \le 2+x^2-\sqrt{x+4}\Leftrightarrow$

και φτάσαμε στο σημείο που για να εμφανιστεί η g πρέπει να διαιρέσουμε με το x.

[box type=»warning»] Προσοχή όμως γιατί,

όταν διαιρούμε μια ανισότητα με αρνητικό αριθμό αλλάζει η φορά της!!! [/box]

κι επειδή δεν γνωρίζουμε τι πρόσημο έχει το x θα διακρίνουμε δυο περιπτώσεις:

Περίπτωση 1η: Για x>0, θα έχουμε

$\frac{2-x^2-\sqrt{x+4}}x \le \frac{f(x)-\sqrt{x+4}}x \le \frac{2+x^2-\sqrt{x+4}}x\Leftrightarrow$

$\frac{2-x^2-\sqrt{x+4}}x \le g(x) \le \frac{2+x^2-\sqrt{x+4}}x$

όμως $\underset{x \to 0}{\mathop{\lim}}\frac{2-x^2-\sqrt{x+4}}x=\underset{x \to 0}{\mathop{\lim}}\frac{2+x^2-\sqrt{x+4}}x= -\frac{1}4$

[wpspoiler name=»Δείτε εδώ γιατί» ]

$\underset{x \to 0}{\mathop{\lim}}\frac{2-x^2-\sqrt{x+4}}x=$

$\underset{x \to 0}{\mathop{\lim}}\frac{(2-x^2-\sqrt{x+4})(2-x^2+\sqrt{x+4})}{x(2-x^2+\sqrt{x+4})}=$

$\underset{x \to 0}{\mathop{\lim}}\frac{(2-x^2)^2-\sqrt{x+4}^2}{x(2-x^2+\sqrt{x+4})}=$

$\underset{x \to 0}{\mathop{\lim}}\frac{4-4x^2+x^4-x-4}{x(2-x^2+\sqrt{x+4})}=$

$\underset{x \to 0}{\mathop{\lim}}\frac{x^4-4x^2-x}{x(2-x^2+\sqrt{x+4})}=$

$\underset{x \to 0}{\mathop{\lim}}\frac{x(x^3-4x-1)}{x(2-x^2+\sqrt{x+4})}=$

$\underset{x \to 0}{\mathop{\lim}}\frac{x^3-4x-1}{2-x^2+\sqrt{x+4}}=$

$\frac{0-0-1}{2-0+\sqrt{0+4}}=-1/4$

Όμοια με την βοήθεια της συζυγούς παράστασης υπολογίζεται και το $\underset{x \to 0}{\mathop{\lim}}\frac{2+x^2-\sqrt{x+4}}{x}=-1/4$ [/wpspoiler] άρα το $\underset{x \to 0^+}{\mathop{\lim}}g(x)=-1/4$ (σχέση 1).

Περίπτωση 2η: Για x<0, θα έχουμε

$\frac{2-x^2-\sqrt{x+4}}x \ge \frac{f(x)-\sqrt{x+4}}x \ge \frac{2+x^2-\sqrt{x+4}}x\Leftrightarrow$

$\frac{2-x^2-\sqrt{x+4}}x \ge g(x) \ge \frac{2+x^2-\sqrt{x+4}}x$

όμως $\underset{x \to 0}{\mathop{\lim}}\frac{2-x^2-\sqrt{x+4}}x=\underset{x \to 0}{\mathop{\lim}}\frac{2+x^2-\sqrt{x+4}}x= -\frac{1}4$ άρα το $\underset{x \to 0^-}{\mathop{\lim}}g(x)=-1/4$ (σχέση 2).

Από τις (σχέση 1) , (σχέση 2) προκύπτει ότι το $\underset{x \to 0}{\mathop{\lim}}g(x)=-1/4$

Να δούμε και την άσκηση 3; ^^^ [/wptabcontent]

[wptabtitle]Άσκηση 3[/wptabtitle] [wptabcontent]Η άσκηση που θα λύσουμε τώρα δεν ανήκει κανονικά σε αυτή τη κατηγορία που εξετάζουμε τώρα αλλά θεώρησα καλό να λύσουμε ένα παράδειγμα επειδή ο τρόπος με τον οποίο λύνεται είναι ίδιος με όλες τις προηγούμενες ασκήσεις. Η άσκηση αυτή αναφέρεται στο πως βρίσκουμε το όριο μιας συνάρτησης η οποία είναι γινόμενο δύο άλλων συναρτήσεων μιας φραγμένης και μιας μηδενικής (δηλαδή έχει όριο ίσο με 0 ). Υπάρχει θεώρημα που δεν διδάσκεται στην Γ΄ Λυκείου που αποδεικνύει ότι «το γινόμενο μιας μηδενικής συνάρτησης επί μία φραγμένη είναι μηδενική». Ας δούμε όμως την άσκηση για να καταλάβουμε τι ακριβώς συμβαίνει.

Άσκηση: Να υπολογιστεί το όριο στο 0 της συνάρτησης $f(x)=x\cdot \eta\mu\frac{1}{x}$

Λύση: Ξεκινώντας να υπολογίσουμε το συγκεκριμένο όριο το πρώτο που σκεφτόμαστε είναι να αντικαταστήσουμε όπου x το 0

singraph — Το ημίτονο είναι φραγμένη συνάρτηση

όμως όπως θα δούμε σε επόμενη δημοσίευση όταν $x \to 0$ τότε $\frac{1}{x} \to \infty$ δυστυχώς δεν γνωρίζουμε το όριο του ημιτόνου στο άπειρο. Για να ξεπεράσουμε αυτό το πρόβλημα θα χρησιμοποιήσουμε το κριτήριο παρεμβολής. Χωρίς να μας έχει δωθεί κάποια διπλή ανισότητα. Δεν πειράζει όμως γιατί για δύο συγκεκριμένες συναρτήσεις την ημx αλλά και την συνx γνωρίζουμε εμείς μια διπλή ανισότητα από προηγούμενες τάξεις. Γνωρίζουμε ότι οι τιμές που παίρνει το ημίτονο και το συνημίτονο δεν μπορούν να βρίσκονται κάτω από το -1 ή πάνω από το 1 (αυτή ακριβώς είναι και η έννοια της φραγμένης συνάρτησης και οι μόνες φραγμένες που έχουμε μάθει είναι αυτές οι δύο το ημίτονο και το συνημίτονο). Πάμε τώρα να εκμεταλλευτούμε αυτή ακριβώς την ιδιότητα της συνάρτησης ημx.

$| \eta\mu \frac{1}{x}| \le 1$

προσπαθούμε τώρα να εμφανίσουμε τη συνάρτηση που μας ενδιαφέρει για το λόγο αυτό θα πολλαπλασιάσουμε όλα τα μέλη της με το |x| (και όχι με το x που δεν ξέρουμε το πρόσημό του κι αναγκαστούμε να πάρουμε περιπτώσεις)

$|x|\cdot |\eta \mu \frac{1}{x}| \le |x| \cdot 1 \Leftrightarrow$

$|x \cdot \eta \mu \frac{1}{x} \le |x| \Leftrightarrow$

$|f(x)| \le |x| \Leftrightarrow$

$-|x| \le f(x) \le |x|$

όμως $\underset{x \to 0}{\mathop{\lim}}(-|x|)=\underset{x \to 0}{\mathop{\lim}}|x|=0$ κι έτσι συμπεραίνουμε από το κριτήριο παρεμβολής ότι $\underset{x \to 0}{\mathop{\lim}}f(x)=0$ .

Είδαμε λοιπόν ότι για τις συναρτήσεις ημx και συνx δεν χρειάζεται να μας δοθεί διπλή ανισότητα την γνωρίζουμε εμείς:
$-1 \le \eta \mu x \le 1 \Leftrightarrow | \eta\mu x| \le 1$

και
$-1 \le \sigma \upsilon \nu x \le 1 \Leftrightarrow |\sigma \upsilon \nu x| \le 1$

[/wptabcontent]

[/wptabs]

Γενικής Παιδείας Γ΄ Λυκείου

Υπάρχουν ασκήσεις στις οποίες ζητείται το όριο μιας συνάρτησης f της οποίας όμως δεν μας έχουν δώσει τον τύπο κι έτσι φαίνεται δύσκολο το να υπολογιστεί το όριο αυτό. Προφανώς όμως κάτι θα μας έχουν δώσει για την συνάρτηση αυτή και συνήθως μας δίνουν είτε ένα όριο στο οποίο συμμετέχει και η συνάρτηση f είτε μια διπλή ανισότητα στο κέντρο της οποίας υπάρχει η f. Αυτές τις δύο περιπτώσεις θα μελετήσουμε εδώ αλλά θα χωρίσουμε το άρθρο στα δύο για δύο κυρίως λόγους πρώτα γιατί προβλέπεται να είναι μεγάλο και θα σας κουράσει και δεύτερον γιατί η πρώτη περίπτωση (δεν δίνεται η f αλλά ένα όριο στο οποίο συμμετέχει η f ) αφορά και τους μαθητές της γενικής παιδείας ενώ η δεύτερη περίπτωση (δεν δίνεται η f αλλά δίνεται διπλή ανισότητα που στο κέντρο της εμφανίζεται η f ) αφορά μόνο μαθητές θετικής και τεχνολογικής κατεύθυνσης.

Ας ξεκινήσουμε λοιπόν με ένα παράδειγμα όπου

μας ζητούν το $\underset{x \to 3}{\mathop{\lim}}f(x)$

καθώς και το $\underset{x \to 3}{\mathop{\lim}} \frac{f(x)-2}{x^2-3x}$

ενώ μας δίνουν ότι ισχύει: $\underset{x \to 3 }{\mathop{\lim }} \frac{f(x)-2x+4}{x-3}=10$

Βλέπουμε λοιπόν εδώ ότι δεν γνωρίζουμε ποια είναι η συνάρτηση f το μόνο που ξέρουμε είναι ένα όριο στο οποίο όμως συμμετέχει και η συνάρτηση f. Θα προσπαθήσουμε λοιπόν να φτιάξουμε έναν «ψεύτικο» τύπο για τη συνάρτηση που μας ενδιαφέρει.

Αυτό το πετυχαίνουμε θεωρώντας σαν συνάρτηση όλο το «περιεχόμενο» του ορίου που μας έχουν δώσει. Δηλαδή, το $\frac{f(x)-2x+4}{x-3}$ το θεωρούμε σαν μια συνάρτηση την οποία και ονομάζουμε g.

Έχουμε τώρα γνωστά δύο πράγματα,

ένα ότι $g(x)=\frac{f(x)-2x+4}{x-3}$ και

δεύτερον ότι το $\underset{x \to 3}{\mathop{\lim}}g(x)=10$

Την πρώτη σχέση την λύνουμε ως προς f(x) και έτσι προκύπτει ο «ψεύτικος τύπος» για την f:

$f(x)=(x-3)g(x)+2x-4$ απ’ όπου θα υπολογίσουμε το όριο της f με τη βοήθεια προφανώς και του γνωστού ορίου της g.

Πράγματι,

$\underset{x \to 3}{\mathop{\lim}}f(x)$ $=\underset{x \to 3}{\mathop{\lim}} (x-3)g(x)+2x-4=0 \cdot 10+2 \cdot 3-4=2$

Ας υπολογίσουμε τώρα και το άλλο όριο,

$\underset{x \to 3}{\mathop{\lim}}\frac{f(x)-2}{x^2-3x}$ παρατηρούμε ότι είναι της μορφής 0/0 (μην ξεχνάμε ότι το όριο της f το βρήκαμε 2). Πρέπει λοιπόν να κάνουμε άρση της απροσδιοριστίας «εμφανίζοντας και εξαφανίζοντας» τον παράγοντα x-3 που ευθύνεται για το 0/0 (καλό είναι να θυμηθείς πως γίνεται αυτό κάνοντας μια γρήγορη ανάγνωση εδώ), έτσι