ΑΛΓΕΒΡΑ Γ΄ ΓΥΜΝΑΣΙΟΥ

![]()
συνήθως την ονομάζουμε τριώνυμο και νομίζω ότι είναι προφανής ο λόγος αφού όπως βλέπουμε αποτελείται από τρεις μόνο όρους. Τον δευτεροβάθμιο όρο «αx2«, τον πρωτοβάθμιο όρο «βx» και από τον σταθερό όρο «γ». Για το τριώνυμο έχουμε ξαναμιλήσει σε προηγούμενο άρθρο κι έχουμε ασχοληθεί με το πως μπορούμε να βρούμε τις ρίζες του, θυμίζουμε ότι ρίζες του τριωνύμου είναι οι λύσεις της εξίσωσης
![]()
(αν θέλετε να το διαβάσετε αναλυτικά κάντε κλικ εδώ αν θέλετε να θυμηθείτε στα γρήγορα τη διαδικασία κάντε κλικ εδώ να δείτε τη μεθοδολογία).
Τώρα θα ασχοληθούμε με το πως μπορούμε να παραγοντοποιήσουμε ένα τριώνυμο δηλαδή με ποιο τρόπο μπορούμε να μετατρέψουμε ένα τριώνυμο σε γινόμενο. Για την παραγοντοποίηση γενικά έχουμε αναφερθεί προηγούμενα εδώ. Επειδή όμως στο σχολικό βιβλίο η παραγοντοποίηση του τριωνύμου παρουσιάζεται αρκετά αργότερα, δεν το είχαμε αναφέρει καθόλου τότε. Έφτασε λοιπόν η ώρα να ασχοληθούμε και με αυτό το θέμα.
Όταν λοιπόν για κάποιο λόγο χρειαστεί ένα τριώνυμο να το κάνουμε γινόμενο δεν έχουμε παρά να βρούμε τις ρίζες του έστω x1 και x2 και στη συνέχεια να χρησιμοποιήσουμε τον τύπο:
[su_note color=»#0972FB»]
[/su_note]![]()
Ας δούμε ένα παράδειγμα: Έστω ότι θέλουμε να μετατρέψουμε σε γινόμενο το ![]() .
.
Πρώτα απ’ όλα πρέπει να βρούμε τις ρίζες του και για το λόγο αυτό λύνουμε την εξίσωση
![]()
.
Έχουμε 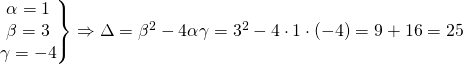
οπότε οι ρίζες είναι
![]()
![]()
Σύμφωνα με αυτά που αναφέραμε πιο πάνω παραγοντοποιούμε το τριώνυμο με τον τύπο και παίρνουμε
![]()
θα δούμε και δύο ακόμη παραδείγματα γιατί πιθανόν να δημιουργήθηκαν απορίες σε ορισμένους από εσάς για το τι κάνουμε στην περίπτωση που δεν έχουμε ρίζες ή στην περίπτωση που το τριώνυμο έχει διακρίνουσα ίση με μηδέν.
Αν ένα τριώνυμο όπως για παράδειγμα το x2+x+1 έχει διακρίνουσα αρνητική (Δ=-3) τότε όπως γνωρίζουμε δεν έχει ρίζες κι έτσι δεν μετατρέπεται σε γινόμενο.
Ενώ αν μας δωθεί για παραγοντοποίηση ένα τριώνυμο όπως το 4x2-12x+9 θα έχουμε
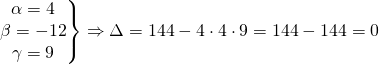
πράγμα που σημαίνει ότι έχουμε δύο ρίζες μόνο που στην περίπτωση αυτή θα είναι ίσες μεταξύ τους. Πράγματι
![]()
Έτσι χρησιμοποιώντας τον τύπο που δώσαμε παραπάνω παίρνουμε τελικά
![]()
το οποίο μάλλον θα ήταν πιο όμορφο αν το γράφαμε έτσι
![]()
![]()
![]()
![]()
![]()
Παρατηρούμε λοιπόν ότι ο τύπος για την παραγοντοποίηση τριωνύμου «δουλεύει» και όταν Δ>0 (δύο ρίζες διαφορετικές) αλλά και όταν Δ=0 (δύο ρίζες ίσες). Αν και όπως βλέπουμε κι από το προηγούμενο ακριβώς παράδειγμα το![]() μας δείχνει ότι το τριώνυμο ήταν ταυτότητα αλλά δεν το είχαμε προσέξει. Αυτό όμως είναι κανόνας που ισχύει πάντα «όταν η διακρίνουσα ενός τριωνύμου είναι ίση με μηδέν το τριώνυμο έχει δύο ρίζες ‘ισες χ1=χ2« κι επομένως θα ισχύει
μας δείχνει ότι το τριώνυμο ήταν ταυτότητα αλλά δεν το είχαμε προσέξει. Αυτό όμως είναι κανόνας που ισχύει πάντα «όταν η διακρίνουσα ενός τριωνύμου είναι ίση με μηδέν το τριώνυμο έχει δύο ρίζες ‘ισες χ1=χ2« κι επομένως θα ισχύει
![]()
Συνοψίζοντας λοιπόν όλα τα παραπάνω έχουμε:
[su_box title=»Μετατροπή τριωνύμου σε γινόμενο» color=»#0972FB»]
Το τριώνυμο ![]()
[su_list style=»arrow»]
- αν έχει Δ<0, δεν παραγοντοποιείται
- αν έχει Δ=0, γίνεται
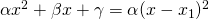
- αν έχει Δ>0, γίνεται
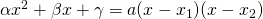
όπου ![]() οι ρίζες του. [/su_list][/su_box]
οι ρίζες του. [/su_list][/su_box]


ΕΤΣΙ ΝΑΙ ΤΟ ΚΑΤΑΛΑΒΑ!!
η παραγοντοποιηση χ2+3χ-4 ..τελειωσε στο αποτελεσμα (χ+4) (χ+1)????
Επισης στη δευτερη παραγοντοποιηση επειδη η Δ=ο πηγατε με α(χ-χ1) (χ-χ2)????
Το τριώνυμο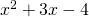 βρήκαμε ότι έχει ρίζες τους 1 και -4 κι άρα σύμφωνα με τον τύπο:
βρήκαμε ότι έχει ρίζες τους 1 και -4 κι άρα σύμφωνα με τον τύπο:
γίνεται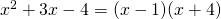 .
.
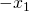 ή
ή 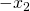 εννοεί τον αντίθετο του χ1 και τον αντίθετο του χ2, γιαυτό και βλέπεις ότι παρότι οι ρίζες είναι 1 και -4 στις παρενθέσεις μέσα έχουν το αντίθετο πρόσημο.
εννοεί τον αντίθετο του χ1 και τον αντίθετο του χ2, γιαυτό και βλέπεις ότι παρότι οι ρίζες είναι 1 και -4 στις παρενθέσεις μέσα έχουν το αντίθετο πρόσημο.
Προσοχή θέλει λίγο στα πρόσημα γιατί όταν ο τύπος λέει
Στην δεύτερη παραγοντοποίηση επειδή η Δ=0 παίρνουμε τον τύπο
κι αφού έχουμε βρεί ρίζα το 3/2 έχουμε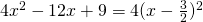 .
.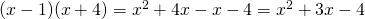
Σε όλες τις περιπτώσεις αφού παραγοντοποιήσεις το τριώνυμο κάνεις αν θες μια επιμεριστική να δεις αν σου βγάζει το αρχικό αποτέλεσμα. π.χ. στο πρώτο παράδειγμα
Ειμαι συναδελφος απο Θεσσαλονικη ) και ενιωσα την αναγκη να σε συσυγχαρω ολοθερμα για τον καταπληκτικο δικτυακο τοπο σου και ευχομαι ναχεις παντα μερακι για να συνεχισεις σ’ αυτην την κατευθυνση.
όταν Δ=0 και α<0 το τριώνυμο είναι τέλειο τετράγωνο;
Όταν Δ=0, το τριώνυμο είναι τέλειο τετράγωνο ανεξάρτητα από το τι είναι το α, θετικό ή αρνητικό (εννοείται 0 δεν μπορεί να είναι για να είναι τριώνυμο).
Διαφωνώ. Όταν Δ=0, όχι δεν είναι τέλειο τετράγωνο κατ’ ανάγκη. Π.χ. η f(x)=-x^2+4x-4=-(x-2)^2 θεωρείται τέλειο τετράγωνο;
Αν Δ=0, σημαίνει ότι υπάρχει μία διπλή ρίζα, όμως δεν είναι κατ’ ανάγκην τέλειο τετράγωνο. Τελειο τετράγωνο είναι ότι μπορείς να εκφράσεις μια ποσότητα ως το τετράγωνο μιας άλλης ποσόστητας. Οι αρνητικοί πώς να γραφτούν σαν τέλειο τετράγωνο; Εκτός αν επιτρέπουμε τους μιγαδικούς συντελεστές.
Γεια σας,
Θα ήθελα να σας ρωτήσω στο κεφάλαιο με τα όρια στην 3 λυκείου όταν έχουμε ένα τριώνυμο να παραγοντοποιήσουμε το οποίο είναι Δ<0, πως το αναλύουμε ώστε να απλοποιηθεί για να συνεχίσουμε την λύση του?
Όταν η διακρίνουσα του τριωνύμου είναι αρνητική τότε το τριώνυμο δεν έχει ρίζες με αποτέλεσμα να μην παραγοντοποιείται.
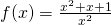 τότε το όριο όταν το χ τείνει στο 0 είναι
τότε το όριο όταν το χ τείνει στο 0 είναι 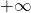 γιατί:
γιατί: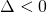 και
και 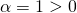 ), ο παρονομαστής κοντά στο 0 είναι θετικός αφού είναι υψωμένος στο τετράγωνο. Άρα το κλάσμα είναι κοντά στο 0 (είτε απο αριστερά είτε από δεξιά) θετικό.
), ο παρονομαστής κοντά στο 0 είναι θετικός αφού είναι υψωμένος στο τετράγωνο. Άρα το κλάσμα είναι κοντά στο 0 (είτε απο αριστερά είτε από δεξιά) θετικό.
Αφού όμως δεν έχει ρίζες το τριώνυμο δεν μηδενίζεται ποτέ και παραμένει πάντα θετικό (αν α>0) ή πάντα αρνητικό (αν α<0).
Υποψιάζομαι ότι η άσκηση που έχεις να λύσεις δεν θα είναι της μορφής 0/0 αλλά το όριο θα βγαίνει + ή - άπειρο κι αυτό εξαρτάται από το πρόσημο που θα έχει το κλάσμα αν λάβεις υπόψη σου και το πρόσημο του τριωνύμου όπως είπαμε παραπάνω.
Η απάντηση στην ερώτησή σου δίνεται "με κάθε επιφύλαξη" γιατί δεν ξέρω για ποια συγκεκριμένη άσκηση μιλάς. εγώ έχω στο μυαλό μου μια άσκηση περίπου έτσι:
α) Ο αριθμητής έχει όριο (στο 0) το 1
β) Ο παρονομαστής έχει όριο το 0
γ) Ο αριθμητής είναι μόνιμα θετικός (τριώνυμο με
θελω βοηθεια!!!
Σε ποια τάξη είσαι Νίκο;
Αν έχεις διδαχθεί το σχήμα Horner θα κάνεις σχήμα Horner με τον αριθμό 1 και θα δεις ότι το 1 είναι ρίζα του πολυωνύμου.
Σε αυτό που θα σου μείνει (πολυώνυμο 3ου βαθμού) θα ξανακάνεις Horner με το 1 και θα δεις ότι και πάλι είναι ρίζα.
Αυτό που θα σου μείνει (πολυώνυμο 2ου βαθμού) θα βρεις τη διακρίνουσα η οποία βγαίνει αρνητική (α=3, β=2, γ=1, Δ=4-12=-8) που σημαίνει ότι δεν υπάρχουν άλλες ρίζες.
Έτσι τελικά η εξίσωση που έχεις έχει μια διπλή ρίζα το 1.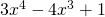 με το
με το 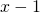 . Η διαίρεση είναι τέλεια και η ταυτότητα της διαίρεσης σου δίνει:
. Η διαίρεση είναι τέλεια και η ταυτότητα της διαίρεσης σου δίνει: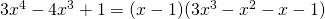
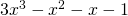 με το χ-1 ξανά και βρίσκεις υπόλοιπο 0 και από την ταυτότητα της διαίρεσης παίρνεις:
με το χ-1 ξανά και βρίσκεις υπόλοιπο 0 και από την ταυτότητα της διαίρεσης παίρνεις: 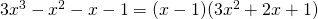
Αν δεν έχεις διδαχθεί το σχήμα Horner θα κάνεις διαίρεση το πολυώνυμο
Τώρα διαιρείς το
Έτσι λοιπόν έχουμε ότι:
ποτε οι ριζες ενος τριωνυμου ειναι ετεροσημες ποτε αντιθετες και ποτε αντιστροφες???
Αν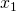 και
και 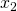 είναι οι λύσεις της εξίσωσης
είναι οι λύσεις της εξίσωσης 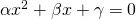 , τότε για να είναι:
, τότε για να είναι:
αντίθετες πρέπει το άθροισμά τους να είναι ίσο με το 0.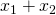 ) που συμβολίζεται με S είναι ίσο με:
) που συμβολίζεται με S είναι ίσο με: 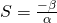 . Πρέπει λοιπόν να ισχύει
. Πρέπει λοιπόν να ισχύει
![Rendered by QuickLaTeX.com \[S=\frac{-\beta}{\alpha}=0\Leftrightarrow\beta=0\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-cad1ab576c7e34cf6b36c72fd89c8742_l3.png)
Όμως από τους τύπους Vieta (ύλη Α΄ Λυκείου) το άθροισμα των ριζών(
αντίστροφες πρέπει το γινόμενό τους να είναι ίσο με 1.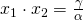 . Πρέπει να ισχύει λοιπόν:
. Πρέπει να ισχύει λοιπόν:
![Rendered by QuickLaTeX.com \[\frac{\gamma}{\alpha}=1\Leftrightarrow\gamma=\alpha\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-6c8940f6ae55e6b82def6a28efa03127_l3.png)
Όμως πάλι από τους τύπους Vieta το γινόμενο των ριζών
ετερόσημες αν ισχύει:![Rendered by QuickLaTeX.com \[x_1\cdot x_2<0\Leftrightarrow\frac{\gamma}{\alpha}<0\Leftrightarrow\gamma\cdot \alpha<0\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-be566cebc22c265b0700f2dcf1b2abbb_l3.png)
δηλαδή με άλλα λόγια όταν οι αριθμοί α και γ είναι ετερόσημοι.
Εχω μπερδευτη με μια ισοτητα Να αποδειξετε την ισοτητα: 5χ – 2χ (3χ-1) – (6χ-1) (1-χ) =1 Μπωρει καποιος να την λυσει και να μου εξηγησει πως;
5χ – 2χ (3χ-1) – (6χ-1) (1-χ) =1
άρα η εξίσωση είναι αόριστη ή ταυτότητα όπως λέγεται γιατί επαληθεύεται για κάθε τιμή του χ.
Ρίξε μια ματιά στα παρακάτω:
Αόριστη και Αδύνατη εξίσωση
Πως λύνω εξισώσεις α’ βαθμού
sugnwmi exw mia eksiswsh alla den mporw na thn lusw : -λ^3 -λ^2 +12λ+82=0.skeftika horner apla epeidi den mporw na vrw profanh lush exw kollisei!isws kapoios gnwrizei!!efxaristw!!
Γεια σας..
Θα ηθελα να με βοηθησετε να λυσω ενα τριωνυμο στο οποιο εχω κολλησει..
4 (χ²+χ+1)= 3χ²+1
Οποιος μπορεσει και με βοηθησει ευχαριστω παρα πολυ !!
Πρώτα βγάζεις παρενθέσεις με τη βοήθεια της επιμεριστικής ιδιότητας:
Τώρα τα μεταφέρεις όλα στο α’ μέλος:
Τώρα με την βοήθεια των τύπων βρίσκεις: α=1, β=4, γ=3 και Δ=4 οπότε οι λύσεις είναι δύο χ= -1 ή χ= -3