Άλγεβρα Γ΄

Quiz Γ΄ Γυμνασίου: Ταυτότητες

Λύστε ένα κουίζ με ασκήσεις Σωστού – Λάθους, Πολλαπλής Επιλογής, Αντιστοίχισης κ.α. με ερωτήσεις από τις Ταυτότητες

Στην Β΄ Γυμνασίου μάθαμε έναν αλγόριθμο (μεθοδολογία) για να επιλύουμε κάθε εξίσωση πρώτου βαθμού.
Τώρα στη Τρίτη τάξη θα δούμε πως μπορούμε κάτω από ορισμένες συνθήκες να βρούμε τις λύσεις και σε άλλες εξισώσεις μεγαλύτερου βαθμού. Η μέθοδος αυτή δεν αποδίδει πάντα, γι’ αυτό αργότερα θα την συμπληρώσουμε

πως μας βοηθά η παραγοντοποίηση στην επίλυση εξισώσεων δεύτερου βαθμού ή μεγαλύτερου.

Πριν όμως από αυτό θα πρέπει να δούμε μια σημαντική ιδιότητα:

$A \cdot\ B=0\Leftrightarrow \left \{ \begin{matrix} A=0\\ \eta\\ B=0 \end{matrix} \right.$

Η οποία μας λέει ότι ένα γινόμενο είναι ίσο με μηδέν τότε και μόνο τότε αν τουλάχιστον ένας από τους παράγοντες του γινομένου είναι ίσος με μηδέν.

Να δούμε τώρα λύνοντας ένα παράδειγμα πως μπορούμε να εκμεταλλευτούμε τα παραπάνω για να βρούμε τις λύσεις σε μια εξίσωση 2ου βαθμού. Έστω λοιπόν ότι ψάχνουμε να βρούμε εκείνους τους αριθμούς που ικανοποιούν τη σχέση $x^2-x=0$ . Αυτή είναι μια δευτεροβάθμια εξίσωση την οποία και θα μετατρέψω σε γινόμενο (με κάποια από τις μεθόδους παραγοντοποίησης που μάθαμε) με σκοπό να χρησιμοποιήσω την ιδιότητα που προαναφέραμε. Έτσι έχουμε

$x^2-x=0\Leftrightarrow$

(βγάζουμε κοινό παράγοντα το x)

$x\cdot(x-1)=0$

φτάσαμε λοιπόν στο σημείο να έχουμε ένα γινόμενο που είναι ίσο με το μηδέν. Το γινόμενο αυτό αποτελείται από δύο (πρωτοβάθμιους) παράγοντες τον x και τον x-1. Σύμφωνα με την ιδιότητα που αναφέραμε παραπάνω συμπεραίνουμε ότι τουλάχιστον ένας από αυτούς τους παράγοντες θα είναι ίσος με μηδέν. Δηλαδή θα ισχύει:

$\left \{ \begin{matrix} x=0\\ \eta\\ x-1=0\Leftrightarrow x=1 \end{matrix} \right.$

Από τον τρόπο που λύθηκε το προηγούμενο παράδειγμα φαίνεται το ποια μέθοδο πρέπει ν’ ακολουθούμε για να επιλύσουμε μια εξίσωση που έχει βαθμό μεγαλύτερο του πρώτου:

[su_label style=»important»]Βήμα 1ο:[/su_label] Μεταφέρουμε όλους τους όρους στο α’ μέλος έτσι ώστε στο δεύτερο μέλος να είναι ίσο με μηδέν.

[su_label style=»success»]Βήμα 2ο:[/su_label] Μετατρέπουμε σε γινόμενο το α’ μέλος.

[su_label style=»warning»]Βήμα 3ο:[/su_label] Παίρνουμε κάθε παράγοντα του γινομένου ίσο με μηδέν.

[su_label style=»info»]Βήμα 4ο:[/su_label] Λύνουμε κάθε μια από τις εξισώσεις (1ου βαθμού) που προκύπτουν από το προηγούμενο βήμα.

Παραγοντοποίηση Τριωνύμου

Με ποιο τρόπο μετατρέπουμε σε γινόμενο ένα τριώνυμο; Τι ρόλο παίζουν οι ρίζες του τριωνύμου σε αυτή τη διαδικασία;

ΑΛΓΕΒΡΑ Γ΄ ΓΥΜΝΑΣΙΟΥ

Παραγοντοποίηση Τριωνύμου — Για να κάνουμε ένα τριώνυμο γινόμενο αρκεί να βρούμε τις ρίζες του χ1 , χ2 και να το γράψουμε α(χ-χ1)(χ-χ2)

Την αλγεβρική παράσταση

$\alpha x^2+\beta x +\gamma$

συνήθως την ονομάζουμε τριώνυμο και νομίζω ότι είναι προφανής ο λόγος αφού όπως βλέπουμε αποτελείται από τρεις μόνο όρους. Τον δευτεροβάθμιο όρο «αx²«, τον πρωτοβάθμιο όρο «βx» και από τον σταθερό όρο «γ». Για το τριώνυμο έχουμε ξαναμιλήσει σε προηγούμενο άρθρο κι έχουμε ασχοληθεί με το πως μπορούμε να βρούμε τις ρίζες του, θυμίζουμε ότι ρίζες του τριωνύμου είναι οι λύσεις της εξίσωσης

$\alpha x^2+\beta x +\gamma=0$

(αν θέλετε να το διαβάσετε αναλυτικά κάντε κλικ εδώ αν θέλετε να θυμηθείτε στα γρήγορα τη διαδικασία κάντε κλικ εδώ να δείτε τη μεθοδολογία).

Τώρα θα ασχοληθούμε με το πως μπορούμε να παραγοντοποιήσουμε ένα τριώνυμο δηλαδή με ποιο τρόπο μπορούμε να μετατρέψουμε ένα τριώνυμο σε γινόμενο. Για την παραγοντοποίηση γενικά έχουμε αναφερθεί προηγούμενα εδώ. Επειδή όμως στο σχολικό βιβλίο η παραγοντοποίηση του τριωνύμου παρουσιάζεται αρκετά αργότερα, δεν το είχαμε αναφέρει καθόλου τότε. Έφτασε λοιπόν η ώρα να ασχοληθούμε και με αυτό το θέμα.

Όταν λοιπόν για κάποιο λόγο χρειαστεί ένα τριώνυμο να το κάνουμε γινόμενο δεν έχουμε παρά να βρούμε τις ρίζες του έστω x₁ και x₂ και στη συνέχεια να χρησιμοποιήσουμε τον τύπο:

[su_note color=»#0972FB»]

$\alpha x^2+\beta x+\gamma=a(x-x_1)(x-x_2)$

[/su_note]

Ας δούμε ένα παράδειγμα: Έστω ότι θέλουμε να μετατρέψουμε σε γινόμενο το $x^2+3x-4$ .

Πρώτα απ’ όλα πρέπει να βρούμε τις ρίζες του και για το λόγο αυτό λύνουμε την εξίσωση

$x^2+3x-4=0$

Έχουμε $\left.\begin{matrix} \alpha=1\\ \beta=3\\ \gamma=-4\end{matrix}\right\}\Rightarrow \Delta=\beta^2-4\alpha\gamma=3^2-4\cdot 1\cdot (-4)=9+16=25$

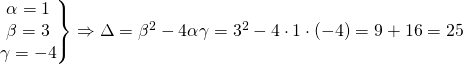
οπότε οι ρίζες είναι

$x_1,x_2=\frac{-\beta\pm\sqrt{\Delta}}{2\alpha}=\frac{-3\pm5}{2}\Rightarrow$ $\left\{\begin{matrix}x_1=\frac{-3-5}{2}=-4\\x_2=\frac{-3+5}{2}=1\end{matrix}$

Σύμφωνα με αυτά που αναφέραμε πιο πάνω παραγοντοποιούμε το τριώνυμο με τον τύπο και παίρνουμε

$x^2+3x-4=1[x-(-4)](x-1)=(x+4)(x-1)$

θα δούμε και δύο ακόμη παραδείγματα γιατί πιθανόν να δημιουργήθηκαν απορίες σε ορισμένους από εσάς για το τι κάνουμε στην περίπτωση που δεν έχουμε ρίζες ή στην περίπτωση που το τριώνυμο έχει διακρίνουσα ίση με μηδέν.

Αν ένα τριώνυμο όπως για παράδειγμα το x²+x+1 έχει διακρίνουσα αρνητική (Δ=-3) τότε όπως γνωρίζουμε δεν έχει ρίζες κι έτσι δεν μετατρέπεται σε γινόμενο.

Ενώ αν μας δωθεί για παραγοντοποίηση ένα τριώνυμο όπως το 4x²-12x+9 θα έχουμε

$\left.\begin{matrix}\alpha=4\\ \beta=-12\\ \gamma=9\end{matrix}\right\}\Rightarrow\Delta=144-4\cdot4\cdot9=144-144=0$

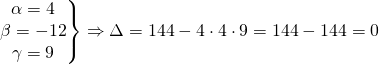
πράγμα που σημαίνει ότι έχουμε δύο ρίζες μόνο που στην περίπτωση αυτή θα είναι ίσες μεταξύ τους. Πράγματι

$x_1=x_2=\frac{-\beta\pm 0}{2a}=\frac{12}{2\cdot4}=\frac{3}{2}$

Έτσι χρησιμοποιώντας τον τύπο που δώσαμε παραπάνω παίρνουμε τελικά

$4x^2-12x+9=4(x-\frac{3}{2})(x-\frac{3}{2})$

το οποίο μάλλον θα ήταν πιο όμορφο αν το γράφαμε έτσι

$4x^2-12x+9=4(x-\frac{3}{2})(x-\frac{3}{2})$

$4x^2-12x+9=4(x-\frac{3}{2})^2$

$4x^2-12x+9=2^2(x-\frac{3}{2})^2$

$4x^2-12x+9=\left\{2(x-\frac{3}{2})\right\}^2$

$4x^2-12x+9=(2x-3)^2$

Παρατηρούμε λοιπόν ότι ο τύπος για την παραγοντοποίηση τριωνύμου «δουλεύει» και όταν Δ>0 (δύο ρίζες διαφορετικές) αλλά και όταν Δ=0 (δύο ρίζες ίσες). Αν και όπως βλέπουμε κι από το προηγούμενο ακριβώς παράδειγμα το $4x^2-12x+9=(2x-3)^2$ μας δείχνει ότι το τριώνυμο ήταν ταυτότητα αλλά δεν το είχαμε προσέξει. Αυτό όμως είναι κανόνας που ισχύει πάντα «όταν η διακρίνουσα ενός τριωνύμου είναι ίση με μηδέν το τριώνυμο έχει δύο ρίζες ‘ισες χ₁=χ₂« κι επομένως θα ισχύει

$\alpha x^2+\beta x+\gamma=\alpha(x-x_1)^2$

Συνοψίζοντας λοιπόν όλα τα παραπάνω έχουμε:

[su_box title=»Μετατροπή τριωνύμου σε γινόμενο» color=»#0972FB»]

Το τριώνυμο $\alpha x^2+\beta x+\gamma$

[su_list style=»arrow»]

αν έχει Δ<0, δεν παραγοντοποιείται
αν έχει Δ=0, γίνεται $\alpha x^2+\beta x+\gamma=\alpha(x-x_1)^2$
αν έχει Δ>0, γίνεται $\alpha x^2+\beta x+\gamma=a(x-x_1)(x-x_2)$

όπου $x_1 , x_2$ οι ρίζες του. [/su_list][/su_box]

Θέλω να μάθω … να λύνω κλασματικές εξισώσεις

Ας δούμε ποια εξίσωση λέγεται κλασματική, πως βρίσκουμε τις λύσεις της και πως τους περιορισμούς. Δείτε πόσο σημαντικό είναι να μην ξεχνάμε να παίρνουμε περιορισμούς κάθε φορά που μια μεταβλητή εμφανίζεται σε παρονομαστή.

Κατ’ αρχάς ας δούμε τι εννοούμε όταν λέμε «κλασματικές εξισώσεις». Πολλοί μπορεί να θεωρούν ότι μια εξίσωση που έχει κλάσματα είναι μια κλασματική εξίσωση. Αυτό όμως δεν είναι σωστό γιατί μια εξίσωση τη λέμε κλασματική μόνο στη περίπτωση που υπάρχει άγνωστος σε ένα τουλάχιστον παρονομαστή της. Έτσι λοιπόν η εξίσωση $\frac{x^2-1}3-\frac{x+3}5=x-2$ ναι μεν έχει κλάσματα αλλά δεν είναι κλασματική αφού δεν υπάρχει άγνωστος σε κανένα παρονομαστή, ενώ η εξίσωση $\frac{6}{x^2+3x}+\frac{x+2}{x}=\frac{x+1}{x+3}$ σύμφωνα με αυτά που προαναφέραμε είναι μια κλασματική εξίσωση αφού ο άγνωστος x «κυκλοφορεί» σε παρονομαστές. Δηλαδή ο x «δουλεύει υπογείως (ύπουλα)» πράγμα επικίνδυνο όπως θα δούμε παρακάτω.

Στη συνέχεια θα επιλύσουμε μια κλασματική εξίσωση για να δούμε ποια μέθοδο ακολουθούμε και τι πρέπει να προσέξουμε.

Να βρείτε τις λύσεις της παρακάτω εξίσωσης $\frac{6}{x^2+3x}+\frac{x+2}{x}=\frac{x+1}{x+3}$

[wptabs mode=»horizontal»] [wptabtitle] Επίλυση[/wptabtitle] [wptabcontent]


$\frac{6}{x^2+3x}+\frac{x+2}{x}=\frac{x+1}{x+3}$ Όπως σε όλες τις κατηγορίες εξισώσεων το πρώτο πράγμα που πρέπει να κάνουμε είναι να απαλλαγούμε από τους παρονομαστές (αν υπάρχουν)
$\frac{6}{x(x+3)}+\frac{x+2}{x}=\frac{x+1}{x+3}$ Για να το πετύχουμε αυτό πρέπει να παραγοντοποιήσουμε όσους από τους παρονομαστές παραγοντοποιούνται. Στην άσκησή μας ο μόνος που μπορεί να παραγοντοποιηθεί είναι ο $x^2+3x=x(x+3)$ (βγάλαμε κοινό παράγοντα το x). Στη συνέχεια αντικαθιστούμε τους παρονομαστές με τους νέους τους παραγοντοποιημένους.
$x(x+3)\frac{6}{x(x+3)}+x(x+3)\frac{x+2}{x}=x(x+3)\frac{x+1}{x+3}$ Τώρα είμαστε σε θέση να βρούμε το Ε.Κ.Π., που είναι το γινόμενο όλων των παρονομαστών με την προϋπόθεση όμως κάθε παράγοντας να εμφανίζεται μία μόνο φορά και μάλιστα στη μεγαλύτερη δύναμη. Στο παράδειγμά μας το Ε.Κ.Π.=χ(χ+3). Πολλαπλασιάζουμε τώρα όλους τους όρους της εξίσωσης με το Ε.Κ.Π.
$6+(x+3)(x+2)=x(x+1)$ Μετά από τις απλοποιήσεις έχουμε μια εξίσωση χωρίς παρονομαστές, όπως φαίνεται δίπλα. Σειρά τώρα για «αποχώρηση» έχουν οι παρενθέσεις ώστε να απελευθερώσουμε το x. Αυτό γίνεται με τη βοήθεια της επιμεριστικής ιδιότητας
$6+x^2+2x+3x+6=x^2+x$ $6+x^2+5x+6=x^2+x$ $12+4x=0$ $4x=-12$ $x=-\frac{12}4$ Συμμαζεύοντας λίγο (κάνουμε αναγωγή όμοιων όρων) θα προκύψει μια εξίσωση 1ου (οπότε χωρίζουμε γνωστούς – άγνωστους κτλ) ή 2ου βαθμού (τα μεταφέρουμε όλα στο ένα μέλος, υπολογίζουμε τη διακρίνουσα κτλ). Στην άσκηση που προσπαθούμε να λύσουμε τώρα παρότι δείχνει δεύτερου βαθμού (αφού έχει x²) αν τη δουλέψουμε λίγο θα δούμε ότι μετά την αναγωγή των όμοιων όρων θα προκύψει μια εξίσωση πρώτου βαθμού οπότε
$x=-3$ βρίσκουμε τελικά πως η εξίσωση που μας δόθηκε έχει λύση τον αριθμό -3.

Μετά από αρκετό κόπο θα έλεγα φτάσαμε στο να βρούμε ότι η εξίσωση $\frac{6}{x^2+3x}+\frac{x+2}{x}=\frac{x+1}{x+3}$ έχει λύση το x=-3.

Κι όμως έχουμε κάνει ΜΕΓΑΛΟ ΛΑΘΟΣ κι αν έχεις κάνει το κόπο να φτάσεις μέχρι εδώ καλό θα ήταν να κάνεις κλικ στην καρτέλα «Περιορισμοί» για να δεις ποιο είναι το λάθος που κάναμε και πόσο σοβαρό είναι.

Επιστροφή^^^
[/wptabcontent]

[wptabtitle]Περιορισμοί[/wptabtitle] [wptabcontent]Όταν έχουμε να λύσουμε μια εξίσωση αναζητούμε ποια τιμή (ή ποιες τιμές) μπορεί να πάρει η άγνωστη μεταβλητή έτσι ώστε αν την αντικαταστήσουμε στην εξίσωση να προκύψει μια αληθής ισότητα (για παράδειγμα η λύση της εξίσωσης 2χ-8=0 είναι ο αριθμός 4 γιατί αν αντικαταστήσουμε το χ με τον αριθμό 4 θα προκύψει 2^.4-8=0 που είναι μια σωστή πρόταση.

Στο προηγούμενο όμως άρθρο είχαμε αναφερθεί στους περιορισμούς (κάντε κλικ εδώ για να το δείτε). Εκεί λοιπόν είπαμε ότι δεν έχει νόημα στα μαθηματικά κλάσμα με παρονομαστή το 0. Γιαυτό όταν λύνουμε κλασματικές εξισώσεις θα πρέπει εκ των προτέρων να θέτουμε περιορισμούς για τον άγνωστο. Δηλαδή από την αρχή να δηλώνουμε ότι για τον άγνωστο, έστω χ, δεν μπορούμε να δεχτούμε κάποιες τιμές γιατί μηδενίζουν κάποιον από τους παρονομαστές της εξίσωσης.

Κατά την επίλυση μιας εξίσωσης σε όποια κατηγορία κι αν ανήκει αυτή (1ου ή 2ου βαθμού ή και κλασματική) σε κάθε μας βήμα (όταν διώχνουμε παρονομαστές, παρενθέσεις κτλ) δημιουργούμε μια άλλη εξίσωση πιο απλή από την αρχική που έχει ως λύσεις της τις λύσεις της προηγούμενης αλλά πιθανόν να έχει κι άλλες (περισσότερες). Στο τέλος τις επιπλέον λύσεις θα πρέπει να τις απορρίψουμε, να μην τις δεχτούμε δηλαδή ως λύσεις της αρχικής εξίσωσης. Αυτό ακριβώς έχει συμβεί και με την εξίσωση $\frac{6}{x^2+3x}+\frac{x+2}{x}=\frac{x+1}{x+3}$ γιατί στην πορεία πήρε διάφορες μορφές μέχρι που κατέληξε να γίνει 4χ=-12. Εμείς βρήκαμε ότι χ=-3 αυτή όμως η λύση είναι η λύση της 4χ=-12 (γιατί αν βάλουμε όπου χ το -3 προκύπτει μια αληθής πρόταση η 4^.(-3)=-12 και όχι της $\frac{6}{x^2+3x}+\frac{x+2}{x}=\frac{x+1}{x+3}$ γιατί εδώ δεν μπορούμε καν να βάλουμε όπου χ το -3 αφού θα μας μηδενίσει κάποιους παρονομαστές (τον χ²+3χ και τον χ+3).

Τι πρέπει να κάνουμε λοιπόν σε τέτοιες περιπτώσεις;

Πρέπει να παίρνουμε τα μέτρα μας, δηλαδή να παίρνουμε περιορισμούς.

ΚΑΘΕ ΠΑΡΟΝΟΜΑΣΤΗΣ ΠΡΕΠΕΙ ΝΑ ΜΗΝ ΓΙΝΕΤΑΙ ΙΣΟΣ ΜΕ 0

κι επειδή μέσα στο Ε.Κ.Π. είναι «κρυμμένοι» όλοι οι παρονομαστές της εξίσωσης είναι αρκετό να απαιτούμε

ΤΟ Ε.Κ.Π. ΝΑ ΜΗΝ ΓΙΝΕΤΑΙ ΠΟΤΕ ΙΣΟ ΜΕ 0 ( $E.K.\Pi.\neq 0$ ).

Στη συγκεκριμένη επομένως άσκηση θα έπρεπε την ώρα που βρήκαμε το Ε.Κ.Π. να γράφαμε: $E.K.\Pi.=x(x+3)\neq 0$ πράγμα που σημαίνει ότι και το x αλλά και το x+3 πρέπει να είναι διάφορα του 0 δηλαδή με άλλα λόγια δεν μπορούμε να δεχτούμε σαν λύσεις ούτε το 0 αλλά ούτε και το -3. Πιο σύντομα και πιο «μαθηματικά» όλα τα παραπάνω θα μπορούσαν να γραφούν ως εξής:

$E.K. /Pi=x(x+3)\neq 0 \Leftrightarrow$

$x\neq 0 \kappa\alpha\iota x+3\neq 0\Leftrightarrow$

$x\neq 0 \kappa\alpha\iota x\neq -3$

Βλέπουμε λοιπόν ότι η εξίσωση που λύναμε τελικά δεν έχει λύση το -3 , άρα δεν έχει καμία λύση ήταν δηλαδή αδύνατη. Ξεχνώντας όμως τους περιορισμούς «την πατήσαμε». Επιστροφή^^^
[/wptabcontent]

[wptabtitle]Σε Έκτακτη Περίπτωση[/wptabtitle] [wptabcontent]Αν σε κάποια περίπτωση αδυνατούμε να βρούμε τους περιορισμούς είτε γιατί κάποιος δυσκολεύεται είτε γιατί δεν προλαβαίνει (π.χ. σε διαγώνισμα) τότε μπορεί να αποφύγει τα παραπάνω και απλώς να ελέγξει αν οι λύσεις που βρήκε μηδενίζουν το Ε.Κ.Π. και
αν το Ε.Κ.Π. μηδενίζεται, τότε η λύση απορρίπτεται αν όχι γίνεται δεκτή.
Στην άσκησή μας το Ε.Κ.Π. = $x(x+3)$ για x=-3 γίνεται Ε.Κ.Π.=-3^.(-3+3)=-3^.0=0 κι επομένως η λύση x=-3 απορρίπτεται.

Μπορεί να σας κούρασα με την μεγάλη έκταση που είχε το άρθρο αλλά θεωρώ τις κλασματικές εξισώσεις λιγάκι δύσκολες για μαθητές Γ΄ Γυμνασίου αλλά και πολύ σημαντικές για τη συνέχεια. Αυτό που πρέπει να θυμόμαστε τελικά είναι πως οι κλασματικές εξισώσεις λύνονται όπως και όλες οι υπόλοιπες δηλαδή:

διώχνουμε παρονομαστές (πολλαπλασιάζοντας με το Ε.Κ.Π.)
διώχνουμε παρενθέσεις (με επιμεριστική)
συμμαζεύουμε λίγο (αναγωγή όμοιων όρων)

έτσι προκύπτει μια εξίσωση 1ου ή 2ου βαθμού που λύνουμε ανάλογα και

τέλος

ΔΕΝ ΞΕΧΝΑΜΕ ΝΑ ΕΛΕΓΞΟΥΜΕ ΑΝ ΟΙ ΛΥΣΕΙΣ ΠΟΥ ΒΡΗΚΑΜΕ ΠΕΡΝΟΥΝ ΤΟ (CRASH) TEST ΤΩΝ ΠΕΡΙΟΡΙΣΜΩΝ (δηλαδή να μην μηδενίζουν το Ε.Κ.Π.).

[/wptabcontent][/wptabs]

Οι Περιορισμοί στα Μαθηματικά του Γυμνασίου

Όταν μαθαίνουμε κάποιους καινούργιους ορισμούς στα μαθηματικά θα πρέπει να είμαστε πολύ προσεκτικοί, να προσέχουμε και την παραμικρή λεπτομέρεια. Έτσι ξεκινώντας από την πρώτη τάξη όπου μάθαμε τι είναι το κλάσμα (το $\frac{a}{b}$ με $b\neq0$ λέγεται κλάσμα) στον ορισμό δηλώσαμε ότι ο παρονομαστής ενός κλάσματος δεν μπορεί να είναι ποτέ ίσος με το μηδέν. Δεν υπάρχει περίπτωση στην αριθμητική ποτέ να δούμε κάτι τέτοιο $\frac{5}{0}$ . Αριθμητική όμως κάναμε μόνο στο Δημοτικό, στο Γυμνάσιο και στο Λύκειο κάνουμε Άλγεβρα. Η βασική διαφορά που υπάρχει είναι ότι στην αριθμητική χρησιμοποιούμαι μόνο αριθμούς ενώ στην άλγεβρα χρησιμοποιούμε και γράμματα (τις μεταβλητές όπως λέγονται πιο σωστά). Έτσι λοιπόν από ‘δω και πέρα θα συναντήσουμε πάρα πολλές φορές κλάσματα που στον παρονομαστή τους θα περιέχουν και μεταβλητές, όπως αυτά $\frac{5}{a}$ , $\frac{a-1}{b-2}$ ή $\frac{13y}{5-x}$ . Στις περιπτώσεις λοιπόν αυτές θα πρέπει να δηλώνουμε δίπλα από κάθε τέτοιο κλάσμα ότι ο παρονομαστής δεν μπορεί να γίνει μηδέν και για να διευκολύνουμε και αυτόν που πρόκειται να διαβάσει αυτό που γράψαμε είναι καλύτερο να γράφουμε ποια τιμή δεν επιτρέπεται να πάρει η μεταβλητή που βρίσκεται στον παρονομαστή που έχουμε. Τα κλάσματα επομένως που γράψαμε παραπάνω το σωστό θα ήταν να τα γράψουμε κάπως έτσι: Continue reading «Οι Περιορισμοί στα Μαθηματικά του Γυμνασίου»

Γραφική Παράσταση Ευθείας – Khan Academy

Μια σειρά ασκήσεων από Khan Academy στην ενότητα Εξίσωση Ευθείας
[khan_exercise src=’static:graphing_linear_equations’ /]

Παραγοντοποίηση

Τι είναι η παραγοντοποίηση;

Παραγοντοποίηση είναι η μετατροπή ενός αριθμού, ή μιας αλγεβρικής παράστασης σε γινόμενο.

Γιά παράδειγμα μπορούμε να παραγοντοποιήσουμε τον αριθμό 12 και να τον γράψουμε 2^.6, αφού 12=2^.6. Οι αριθμοί 2 και 6 λέγονται παράγοντες (ή διαιρέτες) του 12. Με την ανάλυση αριθμού σε γινόμενο δεν θα ασχοληθούμε εδώ, αυτό το

κάναμε πολλά χρόνια πριν στο Δημοτικό και στη Α΄ Γυμνασίου (θυμηθείτε την ανάλυση ενός σύνθετου αριθμού σε γινόμενο πρώτων παραγόντων, όπου το 12 το γράφαμε $12=2^2\cdot 3$ ). Στο άρθρο αυτό θα δούμε με ποιούς τρόπους μπορούμε μια αλγεβρική παράσταση να τη παραγοντοποιήσουμε, δηλαδή να την μετατρέψουμε σε γινόμενο. Πριν ξεκινήσουμε όμως ας κάνουμε μερικές παρατηρήσεις και πρώτα απ’ όλα να πούμε ότι δεν παραγοντοποιούνται όλες οι αλγεβρικές παραστάσεις άλλες γίνονται γινόμενο κι άλλες όχι. Επίσης να πούμε ότι οι τρόποι που θα παρουσιάσουμε εδώ δεν είναι οι μοναδικοί αλλά είναι μόνο αυτοί που μπορεί να χρησιμοποιήσει ένας μαθητής της Γ΄ Γυμνασίου με αυτά που έχει διδαχθεί μέχρι τώρα και σύμφωνα με τη νέα ύλη (έκδοση light δηλαδή). Για τους μαθητές της Α΄ Λυκείου έχουμε επιπλέον τρόπους και για τους μαθητές της Β΄ Λυκείου ακόμη περισσότερους.

Πως γίνεται η παραγοντοποίηση

Όταν μας δωθεί μια αλγεβρική παράσταση και για κάποιο λόγο πρέπει να την μετατρέψουμε σε γινόμενο ακολουθούμε τα παρακάτω βήματα:

Ελέγχουμε αν μπορούμε να εφαρμόσουμε τη μέθοδο του Κοινού Παράγοντα. Αν ναι έχει καλώς την εφαρμόζουμε και τελειώσαμε (συνήθως) αν όχι τότε πάμε στην
Μέθοδο της Ομαδοποίησης αλλά αν δεν εφαρμόζεται ούτε κι αυτή θα κοιτάξουμε μήπως μπορούμε να
Κάνουμε χρήση των Ταυτοτήτων
Εξετάζουμε μήπως η παράσταση που έχουμε είναι τριώνυμο

Ας δούμε όμως αυτές τις μεθόδους αναλυτικά:

[su_tabs style=1]

[su_tab title=»Κοινός Παράγοντας»]

Στην αλγεβρική παράσταση 2χ+2ψ+14ω, τα 2χ, 2ψ και 14ω λέγονται «όροι» της παράστασης. Στον όρο 2χ οι 2 και χ λέγονται παράγοντες του 2χ, ανάλογα το2 και ψ έιναι οι παράγοντες του 2ψ και οι 14 και ω οι παράγοντες του 14ω.
Παρατηρούμε ότι ο αριθμός 2 είναι «κοινός παράγοντας» αφού εμφανίζεται σε όλους τους όρους. Στους 2χ και 2ψ είναι προφανές ενώ στον όρο 14ω είναι κρυμμένος μέσα στο 14 (14=2^.7).
Όταν λοιπόν στην παράσταση που θέλουμε να μετατρέψουμε σε γινόμενο είμαστε «τυχεροι» και υπάρχει κοινός παράγοντας τότε κάνουμε χρήση της επιμεριστικής ιδιότητας ( α(β+γ)=αβ+αγ ). Έτσι η παράσταση 2χ+2ψ+14ω γίνεται 2χ+2ψ+14ω=2χ+2ψ+2^.7ω=2(χ+ψ+7ω) που έγινε γινόμενο και τελειώσαμε.

Όταν κοιτάμε μήπως υπάρχει κάποιος κοινός παράγοντας, κοιτάμε για κοινό αριθμό ή κοινό γράμμα ή ακόμη και για κοινή παρένθεση. Δείτε τα παραδείγματα παρακάτω:
2χ-αχ+βχ²=χ(2 – α+βχ), κοινός παράγοντας ήταν το χ που υπήρχε παντου αφού 2χ-αχ+βχ²=2χ-αχ+βχχ.
3κ(χ+ψ)+6α(χ+ψ)-12β(χ+ψ)=3(χ+ψ)(κ+2α-4β), κοινός παράγοντας ήταν το 3 που είναι κρυμμένο και στο 6 και στο 12 αλλά και η παρένθεση (χ+ψ).

Παρατηρήσεις:

(α) Για να βρούμε τι θα γράψουμε μέσα στη παρένθεση αφού βγάλουμε τον κοινό παράγοντα, διαιρούμε κάθε όρο με τον κοινό παράγοντα (αν και συνήθως είναι προφανές και δεν κάνουμε τη διαίρεση).

π.χ. Στην παράσταση 4χψ²+2χ²ψ-2χψ κοινός παράγοντας είναι το 2χψ κι έτσι θα γράψουμε 2χψ^.(κάτι). Για να βρούμε αυτό το κάτι κάνουμε 4χψ²/2χψ+2χ²ψ/2χψ-2χψ/2χψ=2ψ+χ-1.
Τελικά 4χψ²+2χ²ψ-2χψ=2χψ(2ψ+χ-1).

(β) Για να ελέγξουμε αν η παραγγοντοποίηση έγινε σωστά μπορούμε να κάνουμε επιμεριστική στο αποτέλεσμα και θα πρέπει οπωσδήποτε να προκύψει το πρώτο μέλος.

Έτσι στο προηγούμενο παράδειγμα έχουμε 2χψ(2ψ+2χ-1)=2χψ^.2ψ+2χψ^.2χ-2χψ^.1=4χψ²+4χ²ψ-2χψ.

(γ) Μερικές φορές είναι χρήσιμο να βγάζουμε κοινό παράγοντα κάποιον αριθμό που μπροστά του να έχει πρόσημο – . Σε αυτές τις περιπτώσεις οι όροι που παραμένουν στην παρένθεση έχουν αντίθετο πρόσημο από αυτό που είχαν. Για παράδειγμα στην παράσταση 2χ – 2ψ μπορώ να βγάλω κοινό παράγοντα το 2 και να γίνει 2χ – 2ψ=2(χ-ψ) αλλά θα μπορούσα να βγάλω κοινό παράγοντα και το -2, αν το ήθελα, τότε θα είχαμε 2χ – 2ψ = -2(-χ+ψ).

(δ) Αν κάποιος παράγοντας εμφανίζεται με διαφορετικές δυνάμεις επιλέγουμε να βγάλουμε κοινό παράγοντα αυτόν με τη μικρότερη δύναμη. π.χ. 2α³(χ+ψ)²+4α²(χ+ψ)³=2α²(χ+ψ)²(α+2(χ+ψ))=2α²(χ+ψ)²(α+2χ+2ψ).

[/su_tab]

[su_tab title=»Ομαδοποίηση»]

Επειδή δεν θα είμαστε πάντα τυχεροί να έχουμε κοινό παράγοντα όπως στην περίπτωση της παράστασης 2αχ+4αψ+3βχ+6βψ, τότε κοιτάμε μήπως αν χωρίσουμε τους όρους σε ομάδες καταφέρουμε να βρούμε κοινό παράγοντα. Πράγματι οι όροι 2αχ και 4αψ έχουν κοινό παράγοντα το 2α, οπότε 2αχ+4αψ=2α(χ+2ψ), ενώ οι όροι 3βχ και 6βψ έχουν κοινό παράγοντα το 3β, οπότε 3βψ+6βψ=3β(χ+2ψ). Για να δούμε τι μπορούμε να κάνουμε τώρα, μέχρι στιγμής έχουμε 2αχ+4αψ+3βχ+6βψ=2α(χ+2ψ)+3β(χ+2ψ). Οι όροι από 4 έγιναν 2 και μάλιστα έχουν κοινό παράγοντα την παρένθεση (χ+2ψ), άρα

2αχ+4αψ+3βχ+6βψ=2α(χ+2ψ)+3β(χ+2ψ)=(χ+2ψ)(2α+3β).

Η μέθοδος που ακολουθήσαμε εδώ λέγεται «ομαδοποίηση» ή παραγοντοποίηση κατά ομάδες και ο λόγος είναι προφανής αφού αναγκαστήκαμε να χωρίσουμε την παράσταση σε ομάδες και να βγάλουμε κοινό παράγοντα σε κάθε ομάδα χωριστά.

Παρατηρήσεις:

(α) Στη μέθοδο της ομαδοποίησης ποτέ δεν τελειώνουμε αμέσως αλλά υπάρχουν πάντα δύο στάδια. Αφού τελειώσουμε την παραγοντοποίηση κάθε ομάδας πρέπει οι παρενθέσεις που θα μείνουν να είναι ίδιες ώστε να ξαναβγεί κοινός παράγοντας.

(β) Αν οι παρενθέσεις που θα μείνουν κατά το πρώτο στάδιο δεν είναι ίδιες μάλλον έχουμε διαλέξει λάθος ομάδες. Ξαναδοκιμάζουμε λοιπόν παίρνοντας διαφορετικές ομάδες. π.χ. Για να παραγοντοποιήσω την αχ³+2αβ+βχ²+2α²χ κάνω τα εξής: αχ³+2αβ+βχ²+2α²χ=(αχ³+2αβ)+(βχ²+2α²χ)=α(χ³+2β)+χ(βχ+2α²) και δεν μπορώ να συνεχίσω στο δεύτερο στάδιο αφού οι παρενθέσεις δεν είναι ίδιες κι επομένως δεν έχω κοινό παράγοντα. Αν όμως διαλέξουμε διαφορετικές ομάδες: αχ³+2αβ+βχ²+2α²χ=(αχ³+βχ²)+(2αβ+2α²χ)=χ²(αχ+β)+2α(β+αχ)=(αχ+β)(χ²+2α) είμαστε εντάξει.

(γ) Αν οι παρενθέσεις που θα μας μείνουν κατά το πρώτο στάδιο της παραγοντοποίησης κατά ομάδες είναι αντίθετες αυτό διορθώνεται εύκολα αρκεί να βγάλουμε κοινό παράγοντα τον αντίθετο από αυτό που βγάλαμε. Δείτε το χ³ – χ² – 2χ +2=χ²(χ-1)+2(-χ+1). Οι παρενθέσεις είναι αντίθετες, το διορθώνω είτε βγάζοντας κοινό παράγοντα στη πρώτη ομάδα το – χ² αντί για το χ² είτε το -2 στη δεύτερη ομάδα αντί γιά το 2 κι έτσι θα έχουμε χ³ – χ² – 2χ +2=χ²(χ-1)+2(-χ+1)=χ²(χ-1) – 2(χ-1)=(χ-1)(χ² – 2).

[/su_tab]

[su_tab title=»Ταυτότητες»]

Αν τελικά είμαστε πολύ «άτυχοι» και οι δύο προηγούμενοι τρόποι δεν μπορούν να εφαρμοστούν ελέγχουμε μήπως στην παράσταση υπάρχουν ταυτότητες που μπορούμε να χρησιμοποιήσουμε. Πιο συγκεκριμένα οι ταυτότητες που πιθανόν να υπάρχουν είναι αυτές που διδαχθήκαμε φέτος, δηλαδή οι:

άθροισμα ή διαφορά στο τετράγωνο
$a^2\pm2ab+b^2=(a\pm b)^2$

(1)
άθροισμα ή διαφορά στο κύβο
$a^3\pm3a^2b+3ab^2\pm b^3=(a\pm b)^3$

(2)
διαφορά τετραγώνων
$a^2-b^2=(a-b)(a+b)$

(3)

Μια ένδειξη για το ποια ταυτότητα μπορεί να υπάρχει στην παράσταση αποτελεί το πλήθος των όρων που υπάρχουν στην παράσταση.Έτσι αν υπάρχουν 2 όροι πιθανόν να έχουμε την ταυτότητα (3), αν υπάρχουν 3 όροι πιθανόν να υπάρχει η ταυτότητα (1) και τέλος με 4 όρους ίσως να «παίζει» η ταυτότητα (2). π.χ. Θέλουμε να παραγοντοποιήσουμε την παράσταση x² – 10x+25 και κοινός παράγοντας δεν υπάρχει, σε ομάδες δεν μπορούμε να η χωρίσουμε θα ελέγξουμε την περίπτωση των ταυτοτήτων. Βλέπουμε ότι έχουμε 3 όρους οπότε υποψιαζόμαστε την ταυτότητα a² – 2ab+b². Παρατηρώντας την παράσταση (κι αφού ξέρω τι ψάχνω να βρω) βλέπω το x² και το 5²(=25) και γι’ αυτό το λόγο δοκιμάζω την (x – 5)² που μου δίνει x² – 2^.x^.5+5²=x² – 10x+25. Βγήκε αυτό που ελπίζαμε άρα μπορούμε τώρα να γράψουμε x² – 10x+25=(x – 5)².

[/su_tab]

[su_tab title=»Συνδυασμοί»]

Να σημειώσουμε εδώ ότι οι τρεις μέθοδοι που παρουσιάστηκαν προηγουμένως είναι οι συνηθέστεροι αλλά όπως αναφέραμε και πιο πάνω δεν είναι οι μοναδικοί και ότι υπάρχουν ασκήσεις που χρειάζεται να συνδυάσουμε τις παραπάνω μεθόδους ή και να αυτοσχεδιάσουμε καμιά φορά. Ας δούμε δύο τέτοιες περιπτώσεις:

π.χ.1 Για να παραγοντοποιήσω την παράσταση x²+5x+6, βλέπω ότι δεν υπάρχει κοινός παράγοντας σε ομάδες δεν χωρίζεται (γιατί έχω μόνο 3 όρους ) αλλά ούτε ταυτότητες υπάρχουν. Παρ’ όλα αυτά θα μπορούσαμε να κάνουμε ένα τέχνασμα ώστε οι όροι από 3 να γίνουν 4 κι έτσι να δουλέψω με την μέθοδο της ομαδοποίησης. Σπάω λοιπόν τον όρο 5x σε 2x+3x (επέλεξα αυτά τα νούμερα γιατί είναι «κρυμένα» μέσα στο 6 που έχω στην παράσταση, μην παραλείψετε να διαβάσετε την «Παρατήρηση» στο τέλος του άρθρου). Τώρα να δούμε τι πετύχαμε

$x^2+5x+6=x^2+2x+3x+6=$

$x(x+2)+3(x+2)=(x+2)(x+3)$

Παρατήρηση: Το ότι επιλέξαμε να σπάσουμε το 5χ σε 2χ+3χ όπως αναφέρθηκε και παραπάνω δεν ήταν τυχαίο. Είναι μια ολόκληρη μέθοδος που την παρουσιάζει και το σχολικό βιβλίο ως η «μέθοδος τριωνύμου» που με λίγα λόγια λέει το εξής:
Όταν θέλω να μετατρέψω σε γινόμενο μια παράσταση της μορφής $x^2+Ax+\Gamma$ προσπαθώ να βρω δυο αριθμούς που αν τους προσθέσω να κάνουν Α ενώ αν τους πολλαπλασιάσω να κάνουν Γ. Αν καταφέρω να βρω αυτούς τους αριθμούς, έστω ότι αυτοί είναι ο κ και ο λ, τότε το τριώνυμο παίρνει τη μορφή $(x+\kappa)(x+\lambda)$ . Έτσι λοιπόν στο παραπάνω παράδειγμα είχαμε:

Για το τριώνυμο $x^2+5x+6$ αναζητούμε ένα ζευγάρι αριθμών που θα πρέπει να έχει γινόμενο ίσο με 6 και άθροισμα ίσο με 5. Πριν απαντήσουμε αμέσως ποιοι είναι αυτοί οι αριθμοί ας σκεφτούμε λίγο:

Ξεκινάμε από το γινόμενο διότι υπάρχουν λίγες απαντήσεις. Ενώ άθροισμα 5 μπορώ να σχηματίσω με άπειρα ζευγάρια ακεραίων (π.χ. (2,3) , (6,-1) , (100,-95) κ.α.) , γινόμενο 6 μπορώ να σχηματίσω μόνο με τους: (1,6) , (2,3) , (-1,-6) και (-2,-3).
Από τα παραπάνω ζευγάρια μόνο το ζευγάρι 2 και 3 πληροί τις προϋποθέσεις που έχουμε αφού το άθροισμά τους είναι 5 το δε γινόμενό τους είναι 6.
Άρα έχουμε $x^2+5x+6=(x+2)(x+3)$

Τα παραπάνω μπορούμε να τα τακτοποιήσουμε και σε ένα πινακάκι ως εξής:

$x^2+5x+6=(x+\kappa)(x+\lambda)$
κ	λ	Γινόμενο = +6	Άθροισμα = +5
+1	+6	+6	+7
+2	+3	+6	+5
-1	-6	+6	-7
-2	-3	+6	-5
$x^2+5x+6=(x+2)(x+3)$

Αυτή τη μέθοδο την παρουσιάζουμε εδώ συνοπτικά και δεν χρειάζεται να επιμείνουμε άλλο γιατί σε μερικά μαθήματα παρακάτω θα μάθουμε μια άλλη μέθοδο παραγοντοποίησης του τριωνύμου η οποία δεν παρουσιάζει τους περιορισμούς που παρουσιάζει αυτή η μέθοδος (όπως για παράδειγμα ότι εφαρμόζεται μόνο στην περίπτωση που ο συντελεστής του x² είναι 1)

π.χ.2 Έστω ότι θέλω να παραγοντοποιήσω την παράσταση x⁴-x³+x² – 1. Αφού δεν υπάρχει κοινός παράγοντας πάμε για ομαδοποίηση με x⁴ – x³ τη μια ομάδα (που έχει κοινό παράγοντα το x³) και x² – 1 την άλλη ομάδα που δεν έχει κοινό παράγοντα αλλά είναι ταυτότητα x² – 1=(x – 1)(x+1). Άρα θα έχω

$x^4-x^3+x^2-1=(x^4-x^3)+(x^2-1)=$

$x^3(x-1)+(x-1)(x+1)=$

$(x-1)(x^3+(x+1))=(x-1)(x^3+x+1)$

[/su_tab]

[su_tab title=»plus»]

Αφού είδαμε κάθε μια μέθοδο χωριστά ίσως θα ήταν καλύτερα τώρα να βλέπαμε την παραγοντοποίηση και με μια άλλη ματιά. Πιο πάνω στο άρθρο αυτό αναφέραμε ότι για να παραγοντοποιήσουμε μια αλγεβρική παράσταση ελέγχουμε με τη σειρά: ΚΟΙΝΟ ΠΑΡΑΓΟΝΤΑ >> ΟΜΑΔΕΣ >> ΤΑΥΤΟΤΗΤΕΣ >> ΤΡΙΩΝΥΜΟ. Όμως από τους όρους που έχει αυτή η αλγεβρική παράσταση κάποιες από τις παραπάνω μεθόδους θα μπορούσαν να αποκλειστούν (π.χ. με 2 όρους δεν μπορείς να κάνεις ομαδοποίηση). Έτσι θα μπορούσαμε να σκεφτόμαστε κι ως εξής:

Παραγοντοποίηση με
2 όρους	3 όρους	4+ όρους
Κοινός Παράγοντας
Ταυτότητα $A^2-B^2$	Τριώνυμο	Ομαδοποίηση
	Ταυτότητα $(A\pm B)^2$	Ταυτότητα $(A\pm B)^3$

[/su_tab]

[/su_tabs]

Βοήθειααα … οι Ταυτότητες!!!

Κάθε φορά που ξεκινάω να διδάξω τις ταυτότητες, βλέπω τους μαθητές να τις αντιμετωπίζουν με φόβο, ίσως και τρόμο, πριν καλά καλά τις δουν. Ακούω επιφωνήματα του στυλ «Αχ», «ΩΩΩχχ», «γιατί μας βασανίζετε κύριε» κτλ. Κι αναρωτιέμαι γιατί αυτή η αντιμετώπιση σε ένα αντικείμενο που είναι τόσο εύκολο μα και τόσο χρήσιμο. Οι ταυτότητες μας «λύνουν τα χέρια» σε πάρα πολλές περιπτώσεις που θέλουμε να κάνουμε πράξεις που με τον κλασσικό τρόπο ( την επιμεριστική ιδιότητα δηλαδή) θα θέλαμε περισσότερο χρόνο, περισσότερες πράξεις και φυσικά με μεγαλύτερη πιθανότητα να κάνουμε λάθος. Έχοντας αυτό το εργαλείο στα χέρια μας αποφεύγουμε τις πράξεις και περνάμε κατ’ ευθείαν στο αποτέλεσμα. Μάλιστα πολλές φορές έχω ακούσει την έκφραση «αφού μπορώ να κάνω επιμεριστική και να βρω το αποτέλεσμα γιατί θα πρέπει να μάθω κάτι καινούργιο;» και αμέσως θυμάμαι τις παλίες νοικοκυρές που αγόρασαν για πρώτη φορά πλυντήριο ( γιατί το απαιτούσαν οι καιροί ) αλλά το χρησιμοποιούσαν για να βάζουν επάνω τη σκάφη και να πλένουν με τον παραδοσιακό τρόπο με τη δικαιολογία ότι αυτά είναι λευκά ή ευαίσθητα και το πλυντήριο θα μου τα χαλάσει. Continue reading «Βοήθειααα … οι Ταυτότητες!!!»

Θέλω να μάθω τι είναι η αλγεβρική παράσταση

Πριν ξεκινήσουμε να πούμε τι είναι η αλγεβρική παράσταση καλό θα ήταν να δούμε πρώτα τι είναι η αριθμητική παράσταση.

Αριθμητική παράσταση

Μία παράσταση που αποτελείται από αριθμούς οι οποίοι συνδέονται μεταξύ τους με τα σύμβολα των πράξεων (πρόσθεση, αφαίρεση, πολλαπλασιασμό, δύναμη και πιθανόν παρένθεση), ονομάζεται αριθμητική παράσταση.
Έτσι αριθμητικές παραστάσεις είναι και οι: $2+3^2-1$ , $3\cdot2^3-(5-4)^3$
Όταν σε μια αριθμητική παράσταση εκτελέσουμε τις πράξεις προκύπτει ένας και μοναδικός αριθμός που λέγεται τιμή της αριθμητικής παράστασης. Στα δύο προηγούμενα παραδείγματα έχουμε:
$2+3^2-1=2+9-1=10$ και $3\cdot2^3-(5-4)^3=3\cdot2^3-1^3=3\cdot8-1=24-1=23$ (Σχόλιο)

Αλγεβρική παράσταση

Όταν όμως σε μια παράσταση εκτός από αριθμούς υπάρχουν και μεταβλητές (γράμματα δηλαδή που παριστάνουν αριθμούς) που συνδέονται μεταξύ τους με τα σύμβολα των πράξεων, τότε λέμε ότι έχουμε μια αλγεβρική παράσταση. Για παράδειγμα, αλγεβρικές παραστάσεις είναι οι
$2x+1$ , $x^2+y-1$ , $x^2+3(x-1)$

Στις αλγεβρικές παραστάσεις μπορούμε να αντικαταστήσουμε τα γράμματα με διάφορους αριθμούς (γι’ αυτό το λόγο λέγονται και μεταβλητές). Όταν σε μια αλγεβρική παράσταση αντικαταστήσουμε τα γράμματα που περιέχει με κάποιους αριθμούς αυτό που θα προκύψει θα είναι μια αριθμητική παράσταση, κι αν στη συνέχεια εκτελέσουμε και τις πράξεις θα καταλήξουμε να έχουμε έναν αριθμό.
Έτσι αν στην αλγεβρική παράσταση $2x+1$ αντικαταστήσουμε το x με τον αριθμό 3, θα έχουμε $2(3)+1=6+1=7$ . Ο αριθμός 7 λέγεται τιμή της παράστασης για x=3. Πιο καλά διαβάζουμε ως εξής: Η τιμή της παράστασης $2x+1$ για x=3 είναι 7.
Με παρόμοιο τρόπο βρίσκουμε ότι η τιμή της παράστασης

$x^2+y-1$

για x=1 και y=2 είναι

$(1)^2+(2)-1=1+2-1=2$

ενώ η τιμή της

$x^2+3(x-1)$

για χ=-4 είναι

$(-4)^2+3((-4) - 1)=16+3(-5)=16-15=1$

Δείτε εδώ βίντεο με θέμα τις αλγεβρικές παραστάσεις

_________________________________

Σχόλιο: Θυμηθείτε τη σειρά με την οποία πρέπει να κάνουμε τις πράξεις

Δυνάμεις
Πολλαπλασιασμοί – Διαιρέσεις
Προσθέσεις – αφαιρέσεις
Στην περίπτωση που υπάρχουν παρενθέσεις ξεκινάμε τις πράξεις μέσα από τις παρενθέσεις αλλά και πάλι με την προηγούμενη σειρά.

__________________________________Επιστροφή

Επίλυση δευτεροβάθμιας εξίσωσης

Αφού είδαμε θεωρητικά το πως μπορούμε να βρούμε τις λύσεις μιας δευτεροβάθμιας εξίσωσης, καλό θα ήταν να το εφαρμόσουμε και στην πράξη

Continue reading «Επίλυση δευτεροβάθμιας εξίσωσης»

Κατηγορία: Άλγεβρα Γ΄

Quiz Γ΄ Γυμνασίου: Ταυτότητες

Εξισώσεις 2+ βαθμού

πως μας βοηθά η παραγοντοποίηση στην επίλυση εξισώσεων δεύτερου βαθμού ή μεγαλύτερου.

Παραγοντοποίηση Τριωνύμου

Θέλω να μάθω … να λύνω κλασματικές εξισώσεις

Οι Περιορισμοί στα Μαθηματικά του Γυμνασίου

Γραφική Παράσταση Ευθείας – Khan Academy

Παραγοντοποίηση

Τι είναι η παραγοντοποίηση;

Πως γίνεται η παραγοντοποίηση

Βοήθειααα … οι Ταυτότητες!!!

Θέλω να μάθω τι είναι η αλγεβρική παράσταση

Αριθμητική παράσταση

Αλγεβρική παράσταση

Επίλυση δευτεροβάθμιας εξίσωσης