Απαλλαγή από τις Απόλυτες Τιμές

Στο άρθρο αυτό θα δούμε με τη βοήθεια μιας άσκησης τι πρέπει να κάνουμε για να απαλλαγούμε από τις απόλυτες τιμές όταν αυτό είναι απαραίτητο.

Κατ΄αρχάς ας θυμηθούμε πως ορίζεται η απόλυτη τιμή ενός αριθμού:
αν a>0
αν a=0
αν a<0

Βλέπουμε λοιπόν ότι για να απαλλαγούμε από τα απόλυτα πρέπει να γνωρίζουμε αν το περιεχόμενο της απόλυτης τιμής είναι θετικό, μηδέν ή αρνητικό γιατί σε κάθε περίπτωση ενεργούμε διαφορετικά.

Για παράδειγμα, αν x<3 τότε κι αυτό γιατί; γιατί μας έχουν δώσει ότι x<3 άρα θα είναι x-3<3-3 x-3<0  (αφαιρέσαμε κι από τα δυο μέλη το 3 ώστε να δημιουργήσουμε στη δοθείσα ανισότητα το περιεχόμενο του απολύτου).

Για να δούμε τώρα μια άσκηση πάνω στο συγκεκριμένο θέμα.

Άσκηση:

Αν -3<x<1 να απλοποιήσετε την παράσταση A=2|x-1|+|x+3|-3|x+4| και στη συνέχεια να λύσετε την εξίσωση .

Λύση:

Για να απλοποιηθεί η παράσταση Α θα πρέπει να φύγουν οι απόλυτες τιμές και μετά να συμμαζευτεί λιγάκι. Για να διώξω τα απόλυτα όμως θα πρέπει να ξέρω το περιεχόμενο κάθε απολύτου τι πρόσημο έχει κι αυτό θα το βρω δουλεύοντας κατάλληλα την ανισότητα που μου έχουν δώσει.

• Για το |x-1|,

  αφού ισχύει -3<x<1 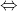-3-1<x-1<1-1 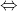-4<x-1<0
  (αφαιρέσαμε κι από τα τρία μέλη της ανισότητας το 1, ώστε να δημιουργηθεί σε αυτήν το περιεχόμενο του απολύτου που μας ενδιαφέρει το x-1 δηλαδή).
  Είδαμε λοιπόν ότι το x-1 είναι αρνητικό κι έτσι σύμφωνα με τον ορισμό της απόλυτης τιμής ξέρω ότι: |x-1|=-(x-1)=(1-x).

• Για το |x+3|,

  γνωρίζω ότι -3<χ<1 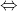-3+3<x+3<1+3 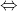0<x+3<4
  δηλαδή x+3 θετικό κι έτσι |x+3|=(x+3).

• Για το |x+4|,

  προφανώς αφού το x+3 είναι θετικό το ίδιο θα ισχύει και για το x+4 που είναι κατά μια μονάδα μεγαλύτερο αλλά ας το δουλέψουμε κι αυτό με τον ίδιο τρόπο.
  -3<x<1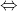-3+4<x+4<1+4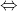1<x+4<5
  κι επομένως |x+4|=(x+4).

Είμαστε τώρα έτοιμοι να δούμε πως θα γίνει η παράσταση Α αφού μπορούμε να αντικαταστήσουμε τις απόλυτες τιμές με αυτά που βρήκαμε παραπάνω. Για να δούμε λοιπόν τι θα προκύψει,

A=2|x-1|+|x+3|-3|x+4|

A=2(1-x)+(x+3)-3(x+4)

A=2-2x+x+3-3x-12

A=-4x-7.

Όσον αφορά τώρα στο άλλο ερώτημα αφού γνωρίζουμε το Α ότι είναι το -4x-7, το αντικαθιστούμε και λύνουμε την εξίσωση που προκύπτει.
Δηλαδή,

   

παρατηρούμε ότι η εξίσωση είναι 2ου βαθμού και για να λυθεί πρέπει να την φέρουμε στη μορφή αχ²+βχ+γ=0. Μεταφέρουμε λοιπόν τα πάντα στο ένα μέλος και κάνουμε το απαραίτητο συμμάζεμα (αναγωγή των όμοιων όρων)

   

ή

   

α=1, β=-5, γ=6 και

   

και

   

   

   

, δηλαδή
ή
Προσοχή όμως στην εκφώνηση έχουμε ότι -3<x<1, οι τιμές λοιπόν που βρήκαμε για το x (2 ή 3) απορρίπτονται και οι δυο. Πράγμα που σημαίνει ότι η εξίσωση που είχαμε να λύσουμε δεν έχει λύσεις είναι δηλαδή «αδύνατη».