Γ ‘ ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ & ΚΑΤΕΥΘΥΝΣΗΣ
Ας φανταστούμε τη συνάρτηση σαν μια “προξενήτρα” μιας και η δουλειά της είναι να “ζευγαρώνει” αριθμούς. Πάρτε για παράδειγμα τη συνάρτηση ![]() η οποία παίρνει τον αριθμό x και τον παντρεύει με τον αριθμό 2x, ζευγαρώνει δηλαδή κάθε αριθμό με τον διπλάσιό του, έτσι δημιουργεί ζεύγη αριθμών όπως το (1,2) αφού για χ=1, δίνει f(1)=2, το (3,6) αφού για χ=3 έχουμε f(3)=6. Η συγκεκριμένη συνάρτηση μπορεί να ζευγαρώσει οποιοδήποτε αριθμό και να της ζητήσουμε. Υπάρχουν όμως συναρτήσεις που δεν μπορούν να το κάνουν αυτό σε όλους τους αριθμούς, έχουν δηλαδή κάποιους περιορισμούς. Ας δούμε για παράδειγμα την
η οποία παίρνει τον αριθμό x και τον παντρεύει με τον αριθμό 2x, ζευγαρώνει δηλαδή κάθε αριθμό με τον διπλάσιό του, έτσι δημιουργεί ζεύγη αριθμών όπως το (1,2) αφού για χ=1, δίνει f(1)=2, το (3,6) αφού για χ=3 έχουμε f(3)=6. Η συγκεκριμένη συνάρτηση μπορεί να ζευγαρώσει οποιοδήποτε αριθμό και να της ζητήσουμε. Υπάρχουν όμως συναρτήσεις που δεν μπορούν να το κάνουν αυτό σε όλους τους αριθμούς, έχουν δηλαδή κάποιους περιορισμούς. Ας δούμε για παράδειγμα την ![]() η οποία “παντρεύει” έναν αριθμό με τον αντίστροφό του, δηλαδή το 5 με το 1/5 αφού g(5)=1/5, το 3/5 με το 5/3 γιατί g(3/5)=5/3 κ.τ.λ.. Το μοναδικό αριθμό όμως που δεν μπορεί να ταιριάξει είναι το 0 γιατί όπως έχουμε μάθει από το Γυμνάσιο ήδη το 0 δεν έχει αντίστροφο (για να μην αναφέρω και το Δημοτικό που μάθαμε ότι δεν ορίζεται διαίρεση με το 0). Όταν λοιπόν μας δίνουν τον τύπο μιας συνάρτησης το πρώτο πράγμα που πρέπει να κάνουμε πριν καν ξεκινήσουμε να την βάλουμε να δουλέψει είναι να βρούμε για ποιούς αριθμούς μπορεί να δουλέψει και για ποιούς όχι. Δεν δίνουμε στη συνάρτηση αριθμούς να παντρέψει χωρίς να δούμε πρώτα αν επιτρέπεται ένας τέτοιος γάμος γιατί υπάρχει περίπτωση αυτός ο γάμος να γεννήσει “τέρατα”. Έτσι λοιπόν όταν μιλάμε για Πεδίο Ορισμού μιας συνάρτησης στη πραγματικότητα εννοούμε το σύνολο των αριθμών που η συνάρτηση μπορεί να πάρει και να τους βρει σύντροφο. Και για να γίνουμε λίγο πιο τυπικοί Πεδίο Ορισμού μιας συνάρτησης f είναι το σύνολο των αριθμών x για τους οποίους υπάρχει το f(x).
η οποία “παντρεύει” έναν αριθμό με τον αντίστροφό του, δηλαδή το 5 με το 1/5 αφού g(5)=1/5, το 3/5 με το 5/3 γιατί g(3/5)=5/3 κ.τ.λ.. Το μοναδικό αριθμό όμως που δεν μπορεί να ταιριάξει είναι το 0 γιατί όπως έχουμε μάθει από το Γυμνάσιο ήδη το 0 δεν έχει αντίστροφο (για να μην αναφέρω και το Δημοτικό που μάθαμε ότι δεν ορίζεται διαίρεση με το 0). Όταν λοιπόν μας δίνουν τον τύπο μιας συνάρτησης το πρώτο πράγμα που πρέπει να κάνουμε πριν καν ξεκινήσουμε να την βάλουμε να δουλέψει είναι να βρούμε για ποιούς αριθμούς μπορεί να δουλέψει και για ποιούς όχι. Δεν δίνουμε στη συνάρτηση αριθμούς να παντρέψει χωρίς να δούμε πρώτα αν επιτρέπεται ένας τέτοιος γάμος γιατί υπάρχει περίπτωση αυτός ο γάμος να γεννήσει “τέρατα”. Έτσι λοιπόν όταν μιλάμε για Πεδίο Ορισμού μιας συνάρτησης στη πραγματικότητα εννοούμε το σύνολο των αριθμών που η συνάρτηση μπορεί να πάρει και να τους βρει σύντροφο. Και για να γίνουμε λίγο πιο τυπικοί Πεδίο Ορισμού μιας συνάρτησης f είναι το σύνολο των αριθμών x για τους οποίους υπάρχει το f(x).
Πως όμως μπορούμε να βρούμε το Πεδίο Ορισμού μιας συνάρτησης;
Αυτό είναι αρκετά απλό θα έλεγα αρκεί να ξέρουμε να λύνουμε εξισώσεις, ανισώσεις και να γνωρίζουμε ποιοί είναι οι
περιορισμοί που προκύπτουν από τον τύπο της συνάρτησης που μας έχει δοθεί. Το να γνωρίζουμε να λύνουμε εξισώσεις και ανισώσεις θα το θεωρήσουμε δεδομένο και θα σταθούμε λίγο στο ποιοι είναι οι περιορισμοί που έχουμε μάθει μέχρι τώρα.
Έτσι λοιπόν όταν μας δοθεί συνάρτηση που να έχει στον παρονομαστή της μεταβλητή (αυτές οι συναρτήσεις λέγονται ρητές) θα πρέπει εμείς να εξαιρέσουμε εκείνους τους αριθμούς που μηδενίζουν τον παρονομαστή της συνάρτησης.
Π.χ.1 Η συνάρτηση ![]() έχει παρονομαστή το 2x-4 πρέπει να δούμε για ποιές τιμές του x μηδενίζεται και να τις εξαιρέσουμε. Για το λόγο αυτό λύνουμε την εξίσωση
έχει παρονομαστή το 2x-4 πρέπει να δούμε για ποιές τιμές του x μηδενίζεται και να τις εξαιρέσουμε. Για το λόγο αυτό λύνουμε την εξίσωση
![]()
και απαντάμε ότι η συγκεκριμένη συνάρτηση έχει Πεδίο Ορισμού όλους τους (πραγματικούς) αριθμούς εκτός από τον αριθμό 2. Πιο καλά είναι να γράφουμε τον τύπο της συνάρτησης και δίπλα τον περιορισμό, δηλαδή ![]() με
με ![]() . Ή ακόμη καλύτερα
. Ή ακόμη καλύτερα ![]() , όπου με Df έχουμε συμβολίσει το Πεδίο Ορισμού της συνάρτησης f. Χρήσιμο είναι όπως θα δείτε αργότερα, όταν θα χρειαστεί να “μελετήσετε” τι ακριβώς δουλειά κάνει η συνάρτηση, να έχετε το Πεδίο Ορισμού σε μορφή διαστημάτων, έτσι σε αυτή τη περίπτωση θα μπορούσαμε να γράψουμε το αποτέλεσμα και ως εξής,
, όπου με Df έχουμε συμβολίσει το Πεδίο Ορισμού της συνάρτησης f. Χρήσιμο είναι όπως θα δείτε αργότερα, όταν θα χρειαστεί να “μελετήσετε” τι ακριβώς δουλειά κάνει η συνάρτηση, να έχετε το Πεδίο Ορισμού σε μορφή διαστημάτων, έτσι σε αυτή τη περίπτωση θα μπορούσαμε να γράψουμε το αποτέλεσμα και ως εξής, ![]() .
.
Π.χ.2 Η συνάρτηση ![]() έχει παρονομαστές τις παραστάσεις:
έχει παρονομαστές τις παραστάσεις:
x+1 η οποία μηδενίζεται για x= –1
(![]() ) και
) και
x2-5x+6 η οποία μηδενίζεται για x=2 ή για x=3
(x2-5x+6=0, Δ=β2-4αγ=1 και ![]() άρα x=2 ή x=3)
άρα x=2 ή x=3)
Η συνάρτηση g λοιπόν δεν μπορεί να δεχτεί στη θέση του x τους αριθμούς {-1,2,3} έτσι λέμε ότι το Πεδίο Ορισμού της είναι όλοι οι πραγματικοί αριθμοί εκτός από αυτούς και γράφουμε ![]() ή
ή![]() .
.
Τελικά καταλήγουμε στο ότι:
[su_box type=»info» title=»Tip 1″ color=»#0000FF»] όταν θέλουμε να βρούμε το πεδίο ορισμού μιας ρητής συνάρτησης της μορφής ![]() λύνουμε την εξίσωση g(x)=0 και γράφουμε Df=R-{οι λύσεις της εξίσωσης g(x)=0}[/su_box]
λύνουμε την εξίσωση g(x)=0 και γράφουμε Df=R-{οι λύσεις της εξίσωσης g(x)=0}[/su_box]
Αν ο τύπος της συνάρτησης που μας έχει δοθεί περιέχει ριζικά που το υπόρριζο (υπόρριζο είναι η παράσταση που βρίσκεται κάτω από το ριζικό) περιέχει μεταβλητή (τέτοιες συναρτήσεις λέγονται άρρητες), τότε απαιτούμε το υπόρριζο να είναι μεγαλύτερο ή ίσο με το 0.
π.χ.1 Η συνάρτηση ![]() ανήκει σε αυτή τη κατηγορία αφού στον τύπο της εμφανίζεται μια τουλάχιστον (τετραγωνική) ρίζα. Το υπόρριζο λοιπόν θα πρέπει να είναι μεγαλύτερο ή ίσο με το 0. Έτσι θα πρέπει να δεχτούμε στο Πεδίο Ορισμού μόνο εκείνες τις τιμές του x για τις οποίες ισχύει:
ανήκει σε αυτή τη κατηγορία αφού στον τύπο της εμφανίζεται μια τουλάχιστον (τετραγωνική) ρίζα. Το υπόρριζο λοιπόν θα πρέπει να είναι μεγαλύτερο ή ίσο με το 0. Έτσι θα πρέπει να δεχτούμε στο Πεδίο Ορισμού μόνο εκείνες τις τιμές του x για τις οποίες ισχύει: ![]() . Συμπεραίνουμε τώρα ότι το Πεδίο Ορισμού της συνάρτησης h είναι:
. Συμπεραίνουμε τώρα ότι το Πεδίο Ορισμού της συνάρτησης h είναι: ![]() .
.
π.χ.2 Στη συνάρτηση ![]() υπάρχουν δύο υπόρριζα (η παράσταση 2x-8 και η παράσταση x-8) και ένας παρονομαστής (η παράσταση
υπάρχουν δύο υπόρριζα (η παράσταση 2x-8 και η παράσταση x-8) και ένας παρονομαστής (η παράσταση ![]() ). Γι’ αυτό το λόγο απαιτούμε τα παρακάτω:
). Γι’ αυτό το λόγο απαιτούμε τα παρακάτω:
![Rendered by QuickLaTeX.com \[\left{\begin{matrix}2x-8\geq 0\Leftrightarrow 2x\geq 8\Leftrightarrow x\geq 4\\ \mathit{\kappa \alpha \iota }\\ x-8\geq 0\Leftrightarrow x\geq 8\\ \mathit{\kappa \alpha \iota }\\ \sqrt{x-8}\neq0\Leftrightarrow x-8\neq0\Leftrightarrow x\neq8\end{matrix}\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-45ac75147f615b071fda201a0c111c99_l3.png)
αλλά όλα αυτά μαζί μας δίνουν x>8 . Επομένως το Πεδίο Ορισμού της συνάρτησης t είναι το ![]() .
.
Καταλήγουμε τελικά στο εξής:
[su_box type=»info» title=»Tip 2″ color=»#0000FF»] όταν θέλουμε να βρούμε το πεδίο ορισμού μιας άρρητης συνάρτησης της μορφής ![]() λύνουμε την ανίσωση
λύνουμε την ανίσωση ![]() και γράφουμε Df={οι λύσεις της ανίσωσης
και γράφουμε Df={οι λύσεις της ανίσωσης ![]() }[/su_box]
}[/su_box]
Στη Β΄ Λυκείου είδαμε για πρώτη φορά τους λογάριθμους και «μελετήσαμε» τη λογαριθμική συνάρτηση ![]() όπου μάθαμε, εκτός των άλλων, ότι το Πεδίο Ορισμού της είναι το
όπου μάθαμε, εκτός των άλλων, ότι το Πεδίο Ορισμού της είναι το ![]() . Γι’ αυτό όταν σε μια συνάρτηση συναντήσουμε λογάριθμο θα πρέπει να αναζητάμε τα x εκείνα για τα οποία το «περιεχόμενο» του λογάριθμου να είναι θετικό. Για παράδειγμα η συνάρτηση
. Γι’ αυτό όταν σε μια συνάρτηση συναντήσουμε λογάριθμο θα πρέπει να αναζητάμε τα x εκείνα για τα οποία το «περιεχόμενο» του λογάριθμου να είναι θετικό. Για παράδειγμα η συνάρτηση ![]() , έχει Πεδίο Ορισμού το σύνολο
, έχει Πεδίο Ορισμού το σύνολο ![]() αφού πρέπει x-6>0 δηλαδή x>6.
αφού πρέπει x-6>0 δηλαδή x>6.
Συμπέρασμα,
[su_box type=»info» title=»Tip 3″ color=»#0000FF»] όταν θέλουμε να βρούμε το πεδίο ορισμού μιας λογαριθμικής συνάρτησης της μορφής ![]() λύνουμε την ανίσωση g(x)>0 και γράφουμε Df={οι λύσεις της ανίσωσης g(x)>0}[/su_box]
λύνουμε την ανίσωση g(x)>0 και γράφουμε Df={οι λύσεις της ανίσωσης g(x)>0}[/su_box]
ΠΑΡΑΤΗΡΗΣΕΙΣ – ΣΧΟΛΙΑ:
- Αν η συνάρτηση της οποίας ζητάμε το Πεδίο Ορισμού δεν έχει ούτε παρονομαστές, ούτε ρίζες, ούτε λογάριθμους που να περιέχουν μεταβλητή, τότε δεν υπάρχουν περιορισμοί κι επομένως το Πεδίο Ορισμού αυτής της συνάρτησης θα είναι όλοι οι πραγματικοί αριθμοί (
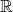 ).
).
π.χ. η ![]() έχει
έχει ![]() αφού δεν υπάρχει x σε παρονομαστή, ρίζα ή λογάριθμο.
αφού δεν υπάρχει x σε παρονομαστή, ρίζα ή λογάριθμο.
- Απ’ την άλλη μεριά όμως αν από τον τύπο μιας συνάρτησης f(x) προκύπτουν περισσότεροι του ενός περιορισμοί, είμαστε υποχρεωμένοι να τους χρησιμοποιήσουμε όλους για να βρούμε ποια είναι τελικά αυτά τα x που πληρούν τις προϋποθέσεις που θέλουμε. Ένα τέτοιο παράδειγμα είδαμε παραπάνω με την συνάρτηση
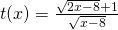 η οποία είχε x και σε παρονομαστή αλλά και σε ρίζες. Στο παράδειγμα αυτό πήραμε τους απαραίτητους περιορισμούς και για τις ρίζες αλλά και για τον παρονομαστή κι αφού λύσαμε τον καθένα ξεχωριστά βρήκαμε την κοινή τους λύση (στην πραγματικότητα λύσαμε ένα σύστημα).
η οποία είχε x και σε παρονομαστή αλλά και σε ρίζες. Στο παράδειγμα αυτό πήραμε τους απαραίτητους περιορισμούς και για τις ρίζες αλλά και για τον παρονομαστή κι αφού λύσαμε τον καθένα ξεχωριστά βρήκαμε την κοινή τους λύση (στην πραγματικότητα λύσαμε ένα σύστημα). - Επειδή στη Γ΄ Λυκείου θα συναντήσουμε πολλές φορές τριγωνομετρικές συναρτήσεις καλό είναι να επισημάνουμε ότι η εφαπτομένη αλλά και η συνεφαπτομένη έχουν παρονομαστές παρότι δεν φαίνονται (αρκεί να θυμηθούμε ότι
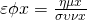 και
και 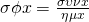 ). Έτσι θα χρειαστεί να πάρουμε τους παρακάτω περιορισμούς:
). Έτσι θα χρειαστεί να πάρουμε τους παρακάτω περιορισμούς:
για την ![]() ,
, ![]() με
με ![]()
για την ![]() ,
, ![]() με
με ![]()
-
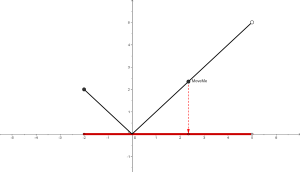
Το Πεδίο Ορισμού της συνάρτησης είναι το κόκκινο διάστημα πάνω στον οριζόντιο άξονα Το Πεδίο Ορισμού μιας συνάρτησης θα μπορούσε να βρεθεί και από τη γραφική παράσταση της συνάρτησης ( στη περίπτωση που δίνεται αυτή ). Για να δείτε πως κάντε κλικ στην εικόνα.
- Για τους μαθητές που παρακολουθούν τα μαθήματα της θετικής ή τεχνολογικής κατεύθυνσης θα πρέπει να αναφέρουμε και δύο ακόμη περιπτώσεις που θα συναντήσουν:
- Συναρτήσεις της μορφής
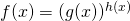 : Πρέπει η βάση g(x) να είναι θετική και διάφορη του 1 (στη περίπτωση που το g(x)=1 ορίζεται η f αλλά είναι σταθερή αφού f(x)=1h(x)=1 για κάθε x)
: Πρέπει η βάση g(x) να είναι θετική και διάφορη του 1 (στη περίπτωση που το g(x)=1 ορίζεται η f αλλά είναι σταθερή αφού f(x)=1h(x)=1 για κάθε x) - Συναρτήσεις οι οποίες έχουν προκύψει από την «σύνθεση» δύο άλλων συναρτήσεων: Για την περίπτωση της «σύνθεσης συναρτήσεων» όμως θα αναφερθούμε αναλυτικά σε άλλο άρθρο.
- Συναρτήσεις της μορφής
Αν θέλετε να κάνετε εξάσκηση στα παραπάνω μπορείτε να κατεβάσετε ένα αρχείο με ασκήσεις κάνοντας κλικ στον παρακάτω σύνδεσμο. Μη διστάσετε να στείλετε τις λύσεις ή να ρωτήσετε τυχόν απορίες , στέλνοντας ένα e-mail ή αφήνοντας ένα σχόλιο στο τέλος του άρθρου.




ΔΑΣΚΑΛΕ καλημέρα και συγχαρητήρια για τη δουλειά και το μεράκι σου. Στις δύσκολες μέρες που περνάμε σαν χώρα ανθρωποι με οράματα και μεράκι για τη δουλειά τους αποτελούν το φάρο μεσα στο σκοτάδι που ίσως μας οδηγήσει να βρούμε ξανά το δρόμο μας. Θεωρώ ότι οι εκπαιδευτικοί πρέπει να έχουν κυρίαρχο ρόλο στη διαμόρφωση μιας κοινωνίας και γι΄αυτό και η αρχική προσφώνηση που κατά την γνώμη μου αποτελεί τίτλο τιμής. Βρέθηκα τυχαία στην ιστοσελίδα σου ψάχνοντας βοήθεια στη μαθηματικά μια και αποφάσισα καθαρά από αγάπη για τη γνώση να ξαναγίνω φοιτητής στα 50 χρόνια μου στο τμήμα πληροφορικής του ΕΑΠ όταν είμαι ήδη Γεωπόνος κάτοχος μεταπτυχιακού τίτλου σπουδών και ειλικρινά ενθουσιάστηκα από την δουλεια σου
Κωστή σε ευχαριστώ για τα καλά σου λόγια. Συγχαρητήρια και για σένα που δεν το βάζεις κάτω, μακάρι να είχα κι εγώ το κουράγιο σου.
thanks!
Καλησπερα, θα ηθελα να σας ρωτησω πως βρισκουμε το πεδιοορισμου αυτης της συναρτησης
f(x)= [ln(x+3)] / [x^2 – 2*|x|]. Γνωριζω οτι το x + 3 >0 kai oti to x^2 – 2*|x|!=0 , αλλα πως συνεχιζουμε απο εδω και περα;
Ευχαριστω για το χρονο σας,
με εκτιμηση Κωνσταντινα
Κωνσταντίνα,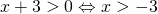 ή αλλιώς
ή αλλιώς 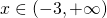 (σχέση 1)
(σχέση 1)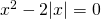 η οποία λύνεται με διάφορους τρόπους εγώ για συντομότερα προτείνω αυτόν: Επειδή το
η οποία λύνεται με διάφορους τρόπους εγώ για συντομότερα προτείνω αυτόν: Επειδή το 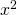 είναι μη αρνητικός αριθμός θα ισχύει
είναι μη αρνητικός αριθμός θα ισχύει 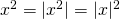 οπότε η εξίσωση γίνεται
οπότε η εξίσωση γίνεται 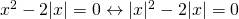 . Βγάζουμε τώρα κοινό παράγοντα το απόλυτο x κι έχουμε:
. Βγάζουμε τώρα κοινό παράγοντα το απόλυτο x κι έχουμε:
Πρώτα λύνεις την ανίσωση
και στη συνέχεια την εξίσωση
Αυτές οι τρεις τιμές πρέπει να αφαιρεθούν από το διάστημα που βρήκαμε στη σχέση 1, κι έστι καταλήγουμε ότι οι επιτρεπτές τιμές για το x είναι οι πραγματικοί αριθμοί που είναι μεγαλύτεροι του -3 εξαιρώντας φυσικα τις τιμές -2, 0 και 2 που μηδενίζουν τον παρονομαστή. Τελικά δηλαδή έχουμε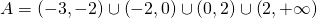
γεια σας , το αρθρο σας ηταν πραγματικα κατατοπιστικο και βοηθησε τοσο εμενα οσο και τος συμμαθητεσ μου και σας ευχαριστουμε θερμα γιαυτο … αλλα θα ηθελα να σασ ρωτησω πως γινεται η διαιρεση συναρτησεων..
σας ευχαριστω εκ των προτερων .. αν μπορουσατε να απαντησετε στο σιγγεκριμενο email θα με βοηθουσατε πολυ …
το ln0 poio ine?
Νίκο δεν ορίζεται το ln0, αν δεις το πεδίο ορισμού της συνάρτησης lnx θα παρατηρήσεις ότι πρέπει το χ να είναι μεγαλύτερο από το 0
Μπορεί κάποιος να μου πει πως σε αυτές βγαίνουνε τα πεδία ορισμού; Πως προκύπτουνε από τα πινακάκια;
http://i.snag.gy/A8sUM.jpg
http://i.snag.gy/p1BVz.jpg
1. Αν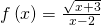 πρέπει να ισχύει:
πρέπει να ισχύει:
Άρα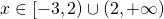
2. Αν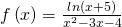 πρέπει:
πρέπει:
Άρα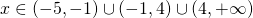
3. Αν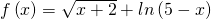 πρέπει
πρέπει
άρα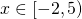
4. Αν![Rendered by QuickLaTeX.com f\left ( x \right )=\frac{\sqrt[3]{13-x}-5}{\sqrt[4]{x+21}}](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-b27d7d97c3c2226b5f324b032ec35592_l3.png) πρέπει
πρέπει 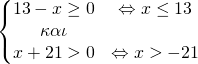 επομένως
επομένως ![Rendered by QuickLaTeX.com x\in (-21,13]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-e953c99b534f04f9b586ddefee0a21ef_l3.png)
Γεια σας και μπραβο για το αρθρο αυτο!
Εχετε καποιο αρθρο για τις συνθεσεις-αποσυνθεσεις κλπ?
Λευτέρη ίσως σε βοηθήσει αυτό: http://mathland.gr/archives/1786
Γεια σας,θα ήθελα να σας ρωτήσω,σε περίπτωση που έχω ένα μόνο κλάσμα,το όποιο στον παρανομαστή έχει τριώνυμο και η διακρίνουσα του βγαίνει αρνητική,τι πεδίου ορισμού έχω?
Καθώς,επίσης,όταν η άσκηση ζητάει να βρω τον πίνακα προσήμων των παρακάτω συναρτήσεων,εννοεί το πεδίο ορισμού της?
Αναστασία, όταν ένα τριώνυμο έχει διακρίνουσα αρνητική, δεν μηδενίζεται ποτέ άρα αφού ο παρανομαστής δεν μηδενίζεται για καμιά τιμή η συνάρτηση θα έχει πεδίο ορισμού όλους τους πραγματικούς αριθμούς.
Όσον αφορά το δεύτερο που ρωτάς δεν μπορώ να σου απαντήσω γιατί δεν καταλαβαίνω ακριβώς τι ζητάει η άσκηση. Αν θες μπορείς να μου τη στείλεις να σου πω.
Καλησπερα σας, θα ηθελα να σας ρωτησω πως βρισκουμε το πεδιο ορισμου της συναρτησης
f(x)=ln(1-e^x) – ln(1+e^x)
Πρέπει
και ταυτόχρονα
που ισχύει πάντα. Άρα η συνάρτηση ορίζεται για χ<0
Γεια σου φίλε μου συγχαρητήρια για την δουλειά σου συνέχισε έτσι…Έχω ένα προβληματάκι προσπαθώ να κατεβάσω αυτό το αρχείο με τις ασκήσεις πατώντας πάνω του αλλά δεν έχω καμία ανταπόκριση μήπως ξέρεις τι μπορεί να ευθύνεται;
Παναγιώτη ευχαριστώ που με ενημέρωσες το διόρθωσα και μπορεις πλέον κάνοντας κλικ να κατεβάσεις το αρχείο.
Αν θες κατεβασέ το κι από εδώ
Εγώ σε ευχαριστώ,καλή συνέχεια στις δουλειές σου!
το e^x=2 ποσο κανει;
Στις εξισώσεις αυτές χρησιμοποιείς τον λογάριθμο. «Λογαριθμίζεις και τα δύο μέλη και έχεις:
και σύμφωνα με ιδιότητα των λογαρίθμων ισχύει: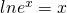 οπότε x=ln2
οπότε x=ln2
Καλημέρα σας και συγχαρητήρια για τη δουλειά που κάνετε.
Εδώ και ώρα, παλεύω με αυτό, γιατί δεν ξέρω τι να κάνω, όταν υπάρχει διάφορο :
Πως βρίσκω το πεδίο ορισμού σε αυτή την περίπτωση;
Νίκο,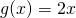 σε κάθε αριθμό αντιστοιχεί τον διπλάσιό του κι έτσι όταν το χ=5 τότε το ψ ή g(x) θα είναι
σε κάθε αριθμό αντιστοιχεί τον διπλάσιό του κι έτσι όταν το χ=5 τότε το ψ ή g(x) θα είναι 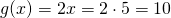 . Έτσι λοιπόν και η συνάρτηση f που έχεις κάνει το ίδιο πράγμα σε κάθε αριθμό χ αντιστοιχεί έναν αριθμό ψ. Πως; όπως περιγράφει ο τύπος της ο οποίος λέει: αν το χ είναι το -1 τότε το «ζευγάρι του» το ψ θα είναι το 1. Αν τώρα το χ είναι οποιοσδήποτε άλλος αριθμός εκτός από το -1, τότε το ζευγάρι του θα είναι ο αριθμός
. Έτσι λοιπόν και η συνάρτηση f που έχεις κάνει το ίδιο πράγμα σε κάθε αριθμό χ αντιστοιχεί έναν αριθμό ψ. Πως; όπως περιγράφει ο τύπος της ο οποίος λέει: αν το χ είναι το -1 τότε το «ζευγάρι του» το ψ θα είναι το 1. Αν τώρα το χ είναι οποιοσδήποτε άλλος αριθμός εκτός από το -1, τότε το ζευγάρι του θα είναι ο αριθμός 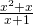 π.χ. όταν χ=1 θα έχουμε
π.χ. όταν χ=1 θα έχουμε 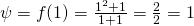 . Βλέπουμε λοιπόν ότι αυτή η συνάρτηση μπορεί να δουλέψει για οποιονδήποτε αριθμό. Αυτό όμως σημαίνει ότι το Πεδίο ορισμού της είναι όλοι οι πραγματικοί αριθμοί (δεν υπάρχει κανένας περιορισμός). Η παραπάνω συνάρτηση όπως βλέπεις κάνει τη δουλεία της (αντιστοίχιση) σε κάθε αριθμό άσχετα αν αλλιώς συμπεριφέρεται στον -1 και αλλιώς στους υπόλοιπους αριθμούς. Σε κάθε συνάρτηση που έχει κλάδους συμβαίνει αυτό, ο κάθε κλάδος μας δείχνει δύο πράγματα: τον τρόπο που γίνεται η αντιστοίχιση και για ποιους αριθμούς γίνεται. Εμείς για να δούμε ποιο είναι το Πεδίο Ορισμού δεν έχουμε παρά να ενώσουμε όλα τα διαστήματα που μας δίνουν οι κλάδοι. Π.χ. αν
. Βλέπουμε λοιπόν ότι αυτή η συνάρτηση μπορεί να δουλέψει για οποιονδήποτε αριθμό. Αυτό όμως σημαίνει ότι το Πεδίο ορισμού της είναι όλοι οι πραγματικοί αριθμοί (δεν υπάρχει κανένας περιορισμός). Η παραπάνω συνάρτηση όπως βλέπεις κάνει τη δουλεία της (αντιστοίχιση) σε κάθε αριθμό άσχετα αν αλλιώς συμπεριφέρεται στον -1 και αλλιώς στους υπόλοιπους αριθμούς. Σε κάθε συνάρτηση που έχει κλάδους συμβαίνει αυτό, ο κάθε κλάδος μας δείχνει δύο πράγματα: τον τρόπο που γίνεται η αντιστοίχιση και για ποιους αριθμούς γίνεται. Εμείς για να δούμε ποιο είναι το Πεδίο Ορισμού δεν έχουμε παρά να ενώσουμε όλα τα διαστήματα που μας δίνουν οι κλάδοι. Π.χ. αν
σε μερικές περιπτώσεις, όπως σε αυτή τη συνάρτηση που μου δίνεις, δεν χρειάζεται να βρεις το Πεδίο Ορισμού γιατί απλά δίνεται αυτό μαζί με τον τύπο της συνάρτησης. Για να το καταλάβεις, καλύτερα να δούμε τι μας λέει ο τύπος της συνάρτησης που έχουμε. Όλες οι συναρτήσεις κάνουν μια «δουλειά», αντιστοιχούν σε κάθε χ κάποιο ψ (ή f(x) αν θες). Με ποιόν τρόπο γίνεται η αντιστοίχηση μας το λέει ο τύπος. Π.χ. η συνάρτηση
τότε Πεδίο Ορισμού είναι: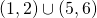
Καλησπερα δασκαλε θα ηθελα να σε ρωτησω αυτο .
F(×)=1προς ριζα χ τετραγωνο πλιν 1 πεδιο ορισμου και διαστημα
Πρέπει η παράσταση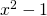 επειδή βρίσκεται μέσα στο ριζικό να είναι μεγαλύτερη ή ίση του μηδενός ταυτόχρονα όμως η ρίζα βρίσκεται στον παρονομαστή ενός κλάσματος κι έτσι δεν πρέπει να μηδενίζεται. Ο συνδυασμός αυτών των δύο περιορισμών μας επιβάλλει να δεχθούμε μόνο εκείνα τα χ για τα οποία η παράσταση
επειδή βρίσκεται μέσα στο ριζικό να είναι μεγαλύτερη ή ίση του μηδενός ταυτόχρονα όμως η ρίζα βρίσκεται στον παρονομαστή ενός κλάσματος κι έτσι δεν πρέπει να μηδενίζεται. Ο συνδυασμός αυτών των δύο περιορισμών μας επιβάλλει να δεχθούμε μόνο εκείνα τα χ για τα οποία η παράσταση 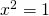 είναι θετική. Έτσι λοιπόν έχουμε να λύσουμε την ανισότητα:
είναι θετική. Έτσι λοιπόν έχουμε να λύσουμε την ανισότητα:
, αυτή λύνεται με διάφορους τρόπους. Στο σχόλιο της Λαμπρινής την λύσαμε με την βοήθεια (τις ιδιότητες) των απολύτων τιμών, εδώ θα τη λύσουμε με άλλο τρόπο: Η εξίσωση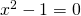 έχει δύο λύσεις το -1 και το 1 (αυτό μπορείς να το βρεις είτε με τη βοήθεια της θεωρίας «δευτεροβάθμια εξίσωση», διακρίνουσα κτλ είτε με παραγοντοποίηση – διαφορά τετραγώνων- κτλ) τώρα που ξέρουμε πότε μηδενίζεται η συγκεκριμένη παράσταση (για x= -1 ή για x=1) μας μένει να βρούμε πότε γίνεται θετική. Αυτό όμως μας το λέει η θεωρία:
έχει δύο λύσεις το -1 και το 1 (αυτό μπορείς να το βρεις είτε με τη βοήθεια της θεωρίας «δευτεροβάθμια εξίσωση», διακρίνουσα κτλ είτε με παραγοντοποίηση – διαφορά τετραγώνων- κτλ) τώρα που ξέρουμε πότε μηδενίζεται η συγκεκριμένη παράσταση (για x= -1 ή για x=1) μας μένει να βρούμε πότε γίνεται θετική. Αυτό όμως μας το λέει η θεωρία: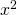 είναι το 1 (θετικός αριθμός) το τριώνυμο
είναι το 1 (θετικός αριθμός) το τριώνυμο 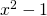 είναι θετικό όταν το x βρίσκεται «έξω» από το διάστημα που ορίζουν οι ρίζες του. Ας θυμηθούμε ότι οι ρίζες του είναι το -1 και το 1, άρα το Πεδίο Ορισμού είναι το
είναι θετικό όταν το x βρίσκεται «έξω» από το διάστημα που ορίζουν οι ρίζες του. Ας θυμηθούμε ότι οι ρίζες του είναι το -1 και το 1, άρα το Πεδίο Ορισμού είναι το 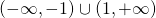
«Ένα πολυώνυμο δεύτερου βαθμού είναι ομόσημο του συντελεστή του μεγιστοβάθμιου όρου στα διαστήμα που βρίσκονται εκτός των ριζών του» δηλαδή στη συγκεκριμένη περίπτωση επειδή ο συντελεστής του
οταν ειναι ln(x+1 / x-1) ποιο ειναι το Df?
Κατ’ αρχάς πρέπει το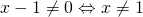 , γιατί δεν πρέπει να μηδενίζεται ο παρονομαστής του κλάσματος. Επίσης το περιεχόμενου του λογάριθμου, δηλαδή το κλάσμα
, γιατί δεν πρέπει να μηδενίζεται ο παρονομαστής του κλάσματος. Επίσης το περιεχόμενου του λογάριθμου, δηλαδή το κλάσμα 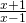 υποχρεούται να είναι θετικό. Έτσι πρέπει να ισχύει:
υποχρεούται να είναι θετικό. Έτσι πρέπει να ισχύει:
δηλαδή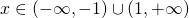 . Από το διάστημα αυτό βλέπουμε ότι λείπει το 1 που ήταν η πρώτη μας απαίτηση κι έτσι καταλήγουμε ότι το Πεδίο Ορισμού είναι το
. Από το διάστημα αυτό βλέπουμε ότι λείπει το 1 που ήταν η πρώτη μας απαίτηση κι έτσι καταλήγουμε ότι το Πεδίο Ορισμού είναι το 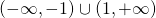
Καλησπερα, θα μπορουσατε να με βοηθησετε με το πεδιο ορισμου της συναρτησης : f(x)=x+ |x^2-1| ;
Κωνσταντίνε,
η συνάρτηση που έχεις δεν έχει κανένα περιορισμό για την μεταβλητή χ (δεν βρίσκεται σε παρονομαστή, δεν βρίσκεται κάτω από ρίζα, δεν βρίσκεται μέσα σε λογάριθμο ούτε μέσα σε εφαπτομένη ή συνεφαπτομένη) επομένως πεδίο ορισμού είναι το σύνολο των πραγματικών αριθμών.
f(x)= ριζα χ2+χ-2 , f(x)= x αριθμητης και 2χ+4 παρονομαστης πως λυνονται ?? εχω κολησει
1)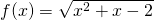 , πρέπει το υπόριζο
, πρέπει το υπόριζο 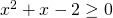 . Για το λόγο αυτό με τη βοήθεια της Διακρίνουσας (που είναι ίση με 9) βρίσκεις τις ρίζες του τριωνύμου που είναι -2 και 1 κι έχεις ότι το τριώνυμο
. Για το λόγο αυτό με τη βοήθεια της Διακρίνουσας (που είναι ίση με 9) βρίσκεις τις ρίζες του τριωνύμου που είναι -2 και 1 κι έχεις ότι το τριώνυμο 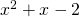 είναι ετερόσημο του α (α είναι ο συντελεστής του
είναι ετερόσημο του α (α είναι ο συντελεστής του 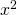 που στην περίπτωσή μας είναι 1) δηλαδή αρνητικό στο διάστημα που βρίσκετε ανάμεσα στις ρίζες -2 και 1. επομένως όταν το x ανήκει στο δίαστημα από -1 μέχρι 2 το τριώνυμο είναι αρνητικό. Εμείς όμως δεν θέλουμε να είναι αρνητικό, το αντίθετο μάλιστα. Έτσι λοιπόν λέμε ότι για να ορίζεται η συνάρτηση πρέπει το υπόριζο να είναι μεγαλύτερο ή ίσο με το μηδέν άρα το x πρέπει να παίρνει τιμές από το μειον άπειρο μέχρι το -1 ή από το 2 μέχρι το συν άπειρο. Δηλαδή Πεδίο Ορισμού είναι το
που στην περίπτωσή μας είναι 1) δηλαδή αρνητικό στο διάστημα που βρίσκετε ανάμεσα στις ρίζες -2 και 1. επομένως όταν το x ανήκει στο δίαστημα από -1 μέχρι 2 το τριώνυμο είναι αρνητικό. Εμείς όμως δεν θέλουμε να είναι αρνητικό, το αντίθετο μάλιστα. Έτσι λοιπόν λέμε ότι για να ορίζεται η συνάρτηση πρέπει το υπόριζο να είναι μεγαλύτερο ή ίσο με το μηδέν άρα το x πρέπει να παίρνει τιμές από το μειον άπειρο μέχρι το -1 ή από το 2 μέχρι το συν άπειρο. Δηλαδή Πεδίο Ορισμού είναι το 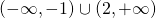
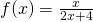 πρέπει ο παρονομαστής να μην γίνεατι ποτλε μηδεν, δηλαδή θέλουμε να ισχύει:
πρέπει ο παρονομαστής να μην γίνεατι ποτλε μηδεν, δηλαδή θέλουμε να ισχύει: 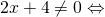
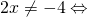
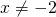 άρα το Πεδίο Ορισμού είναι όλοι οι πραγματικοί αριθμοίεκτός από το -2 γιατί αυτός ο αριθμός μηδενίζει τον παρονομαστή.
άρα το Πεδίο Ορισμού είναι όλοι οι πραγματικοί αριθμοίεκτός από το -2 γιατί αυτός ο αριθμός μηδενίζει τον παρονομαστή.
2)
Το x^e τι πεδιο ορισμου εχει ;
Όλους τους πραγματικούς αριθμούς αφού δεν υπάρχει κανένας περιορισμός για το χ
Στην περιπτωση που εχουμε υποριζο ποσοτητα υψωμενη στο τετραγωνο τοτε παιρνουμε ως πεδιο ορισμου την απολυτη τιμη αυτης μεγαλυτερη η ιση του μηδενος?
Στην περίπτωση αυτή το Πεδίο Ορισμού είναι όλοι οι πραγματικοί αριθμοί αφού κάθε ποσότητα που είναι υψωμένη στο τετράγωνο είναι μεγαλύτερη ή ιση του μηδενός.
Συγχαρητήρια στο άτομο που το επιμελήθηκε!
Ποιο ειναι το πεδιο ορισμου της συναρτησης : f(x)=|x| ?
Είναι όλοι οι πραγματικοί αριθμοί αφού δεν υπάρχει κανένας περιορισμός για το χ. Ούτε παρονομαστή έχουμε (φανερό ή κρυμένο), ούτε ριζικό, ούτε και λογάριθμο.
Μπορει καποιος να μου βρει το πεδιο ορισμου αυτης της συναρτησης: ln(x^2-2x+1)?
Άννα,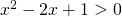 . Η συγκεκριμένη ανίσωση λύνεται με διάφορους τρόπους π.χ. ως δευτεροβάθμια ανίσωση όπου βρίσκεις μέσω της διακρίνουσας (Δ=0) τίς ρίζες (χ=1, διπλή ρίζα) και με το πινακάκι βρίσκεις τα πρόσημα κτλ. Όμως αν την παρατηρήσεις καλύτερα θα δεις ότι η παράσταση
. Η συγκεκριμένη ανίσωση λύνεται με διάφορους τρόπους π.χ. ως δευτεροβάθμια ανίσωση όπου βρίσκεις μέσω της διακρίνουσας (Δ=0) τίς ρίζες (χ=1, διπλή ρίζα) και με το πινακάκι βρίσκεις τα πρόσημα κτλ. Όμως αν την παρατηρήσεις καλύτερα θα δεις ότι η παράσταση 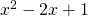 είναι μια ταυτότητα και τελικά παίρνει τη μορφή
είναι μια ταυτότητα και τελικά παίρνει τη μορφή 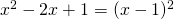 , άρα λοιπόν έχεις να λύσεις την ανίσωση
, άρα λοιπόν έχεις να λύσεις την ανίσωση 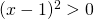 . Θυμήσου όμως ότι κάθε παράσταση που είναι υψωμένη στη δευτέρα δεν μπορεί να είναι αρνητική, επομένως τι θα είναι πάντα; είτε θετική είτε ίση με μηδέν. Εσύ θέλεις, επειδή αυτή η παράσταση είναι μέσα στο λογάριθμο, να είναι θετική. Τι δεν θες λοιπόν; να είναι ίση με μηδέν. Ψάχνεις λοιπόν να δεις πότε η χ-1 γίνεται ίση με μηδέν και εξαιρείς αυτήν την τιμή. Λύνεις δηλαδή την εξίσωση
. Θυμήσου όμως ότι κάθε παράσταση που είναι υψωμένη στη δευτέρα δεν μπορεί να είναι αρνητική, επομένως τι θα είναι πάντα; είτε θετική είτε ίση με μηδέν. Εσύ θέλεις, επειδή αυτή η παράσταση είναι μέσα στο λογάριθμο, να είναι θετική. Τι δεν θες λοιπόν; να είναι ίση με μηδέν. Ψάχνεις λοιπόν να δεις πότε η χ-1 γίνεται ίση με μηδέν και εξαιρείς αυτήν την τιμή. Λύνεις δηλαδή την εξίσωση 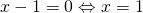 και απαντάς ότι πεδίο ορισμού είναι όλοι οι πραγματικοί αριθμοί εκτός από το 1, γιατί αυτός ο αριθμός μετατρέπει το περιεχόμενο του λογάριθμου σε 0 που δεν επιτέπεται.
και απαντάς ότι πεδίο ορισμού είναι όλοι οι πραγματικοί αριθμοί εκτός από το 1, γιατί αυτός ο αριθμός μετατρέπει το περιεχόμενο του λογάριθμου σε 0 που δεν επιτέπεται.
το περιεχόμενο του λογάριθμου απαιτείται να είναι θετικό. Πρέπει λοιπόν να δεις πότε ισχύει:
καλησπερα ,εχω μια μικρη απορια
οταν π.χ εχω σε ενα κλασμα ριζα στον παρανομαστη για πεδιο ορισμου παιρνω το εσωτερικο της ριζας μονο μεγαλυτερο του μηδενος .. οταν κανω το πινακακι για να βρω το προσημο του υποριζου βαζω και το -απειρο?
Ναι το πινακάκι πρέπει να είναι από μέχρι
μέχρι 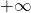 και αυτό γιατί δεν ξέρεις εκ των προτέρων που θα βρίσκονται οι λύσεις μπορεί για παράδειγμα να είναι
και αυτό γιατί δεν ξέρεις εκ των προτέρων που θα βρίσκονται οι λύσεις μπορεί για παράδειγμα να είναι 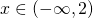 αν ο παρονομαστής είναι η παράσταση
αν ο παρονομαστής είναι η παράσταση 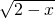 ή και όλο το R αν ο παρονομαστής είναι:
ή και όλο το R αν ο παρονομαστής είναι: 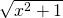
To ln (1+e*x)
Τι πεδιο ορισμου έχει διότι λύνω το μέσα μεγαλύτερο του 0 και βγαίνει e+×>1
Η άσκηση λέει να αποδείξω ότι έχει όλο το R
Πρέπει,
άρα
που ισχύει πάντα (για οποιοδήποτε x ισχύει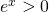 ) άρα αφού δεν υπάρχουν περιορισμοί πεδίο ορισμού είναι όλο το R
) άρα αφού δεν υπάρχουν περιορισμοί πεδίο ορισμού είναι όλο το R
στην περίπτωση f(x)=g(x)^h(x) γιατί πρέπει το g(x) να είναι θετικό;
ευχαριστώ
Ναι
Συγχαρητηρια για τη δουλεια πολυ κατανοητα ολα εγω θα ηθελα το πεδιο ορισμου της f(x)=ln(x/x-1)
Θα πρέπει να είναι
ή
Οι ρίζες του τριωνύμου είναι το μηδέν και το 1, το τριώνυμο είναι θετικό (ομόσημο του α) εκτός των ριζών κι επομένως:
όμως πρέπει να εξαιρέσουμε την τιμή 1 άρα το πεδίο ορισμού είναι: