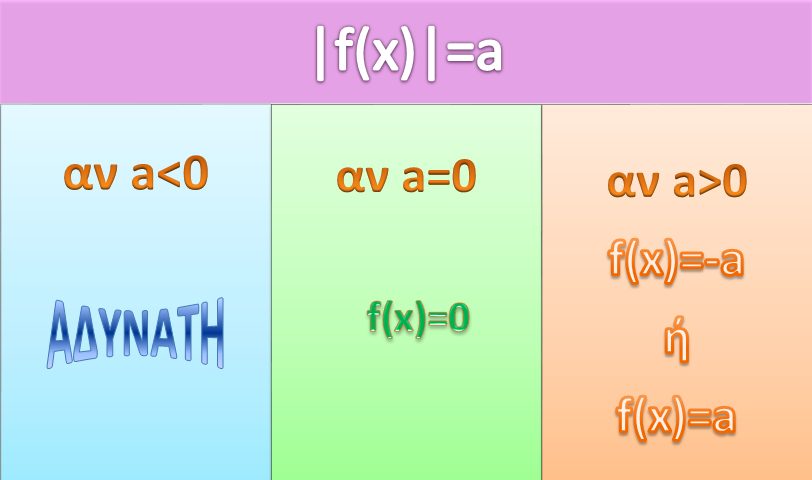Κατηγορία: Θέλω να μάθω…
Θέλω να μάθω … να λύνω εξισώσεις με απόλυτα
Για να λύσουμε εξισώσεις με απόλυτες τιμές (που ο άγνωστος είναι «φυλακισμένος» μέσα σε απόλυτα) πρέπει να ελευθερώσουμε τον άγνωστο από το απόλυτο. Πως μπορούμε να το πετύχουμε;
ΑΛΓΕΒΡΑ Α΄ ΛΥΚΕΙΟΥ
 Για το πως μπορούμε να απαλλαγούμε από τις απόλυτες τιμές που τυχόν εμφανίζονται σε μία αλγεβρική παράσταση έχουμε αναφερθεί σε προηγούμενο άρθρο μας (και καλό θα ήταν να του ρίξετε μια ματιά κάνοντας κλικ εδώ). Σε αυτή τη δημοσίευση θα ασχοληθούμε με εξισώσεις στις οποίες ο άγνωστος βρίσκεται πίσω από τις μπάρες της απόλυτης τιμής. Εξισώσεις δηλαδή που ο άγνωστος είναι «φυλακισμένος» μέσα σε μία ή και περισσότερες απόλυτες τιμές. Σκοπός μας σε μια τέτοια εξίσωση (όπως και σε κάθε εξίσωση άλλωστε) είναι να βρούμε ποιος αριθμός είναι «κρυμμένος πίσω από τη μάσκα του x». Στόχος μας είναι να «ελευθερώσουμε» το x μέσα από την απόλυτη τιμή. Για να το καταφέρουμε αυτό ας θυμηθούμε πρώτα τι είναι η απόλυτη τιμή ενός αριθμού και μετά βλέπουμε πως λύνουμε την εξίσωση.
Για το πως μπορούμε να απαλλαγούμε από τις απόλυτες τιμές που τυχόν εμφανίζονται σε μία αλγεβρική παράσταση έχουμε αναφερθεί σε προηγούμενο άρθρο μας (και καλό θα ήταν να του ρίξετε μια ματιά κάνοντας κλικ εδώ). Σε αυτή τη δημοσίευση θα ασχοληθούμε με εξισώσεις στις οποίες ο άγνωστος βρίσκεται πίσω από τις μπάρες της απόλυτης τιμής. Εξισώσεις δηλαδή που ο άγνωστος είναι «φυλακισμένος» μέσα σε μία ή και περισσότερες απόλυτες τιμές. Σκοπός μας σε μια τέτοια εξίσωση (όπως και σε κάθε εξίσωση άλλωστε) είναι να βρούμε ποιος αριθμός είναι «κρυμμένος πίσω από τη μάσκα του x». Στόχος μας είναι να «ελευθερώσουμε» το x μέσα από την απόλυτη τιμή. Για να το καταφέρουμε αυτό ας θυμηθούμε πρώτα τι είναι η απόλυτη τιμή ενός αριθμού και μετά βλέπουμε πως λύνουμε την εξίσωση.
Η απόλυτη τιμή ενός αριθμού ορίζεται και αλγεβρικά και γεωμετρικά. Εμείς θα αρκεστούμε στο δεύτερο μιας και είναι αρκετό για να στηριχτούμε σε αυτό και να καταφέρουμε να λύσουμε τις εξισώσεις.
Τι είναι λοιπόν η απόλυτη τιμή;
Γνωρίζουμε ότι κάθε πραγματικός αριθμός x παριστάνεται με ένα σημείο πάνω στον άξονα των πραγματικών αριθμών. Την απόσταση του σημείου αυτού από το 0 τη λέμε απόλυτη τιμή του αριθμού x και τη συμβολίζουμε |x|.

Έτσι μπορούμε να εξηγήσουμε και πολλές από τις ιδιότητες της απόλυτης τιμής όπως
Η απόλυτη τιμή οποιουδήποτε αριθμού είναι είτε θετικός αριθμός είτε μηδέν, γιατί όπως είναι γνωστό αρνητική απόσταση δεν υπάρχει. Έτσι έχουμε,
Οι αντίθετοι αριθμοί έχουν την ίδια απόλυτη τιμή, αφού ισαπέχουν από το 0.
Ας δούμε τώρα τι γίνεται με τις εξισώσεις.
Σας θυμίζω ότι για να αντιλαμβανόμαστε καλύτερα τις εξισώσεις μπορούμε να τις θεωρούμε σαν ερωτήσεις. Έτσι η εξίσωση |x|= -5 , μας ρωτάει ποιος αριθμός είναι αυτός που απέχει από το 0 -5 μονάδες; Προφανώς η απάντηση είναι κανένας (αναφέραμε και πιο πάνω ότι δεν νοείται αρνητική απόσταση). Ενώ η απάντηση στην ερώτηση(=εξίσωση) |x|=0 είναι «ο μοναδικός αριθμός που απέχει από το μηδέν 0 μονάδες είναι ο 0». Όμως η εξίσωση |χ|=2 μας ζητάει να βρούμε τον αριθμό που απέχει από το 0 2 μονάδες. Η απάντηση είναι ότι δεν υπάρχει μόνο ένας αριθμός με αυτή την ιδιότητα αλλά δύο αριθμοί ο 2 και ο -2. Έτσι η εξίσωσή μας έχει δύο λύσεις τις x=2 ή x= -2. Για να γενικεύσουμε λίγο τα πράγματα και να τα βάλουμε σε μία τάξη δείτε το παρακάτω σχεδιάγραμμα.

Όπου βλέπετε f(x) θα εννοούμε «μια παράσταση που περιέχει x». Γιατί μέσα στο απόλυτο δεν είναι απαραίτητο να υπάρχει μόνο x, μπορεί κάποιοι «κακοί μαθηματικοί» (σαν κι εμένα) να ζητήσουν να λυθούν εξισώσεις που μέσα στο απόλυτο να υπάρχουν αρκετά πράγματα.
Για να λύσουμε οποιαδήποτε εξίσωση στην οποία το x βρίσκεται μέσα σε απόλυτο, πρέπει να στηριχτούμε στα συμπεράσματα του παραπάνω πίνακα. Πρέπει λοιπόν να απομονώσουμε το απόλυτο στο ένα μέλος και μετά κοιτώντας τι ρόλο παίζει το άλλο μέλος να αποφανθούμε αν η εξίσωση έχει λύσεις ή όχι και στην περίπτωση που έχει ποιες είναι αυτές. Ας δούμε τώρα μερικά παραδείγματα:
Άσκηση 1: Να λυθεί η εξίσωση 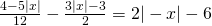
[gn_spoiler title=»Λύση:»]Φαίνεται η εξίσωση μας να έχει δύο διαφορετικές απόλυτες τιμές την |x| και την |-x|. Αυτό όμως δεν αληθεύει γιατί ξέρουμε ότι |-x|=|x|. Οπότε μπορούμε στην εξίσωση που μας δώσανε όπου έχει |-x| εμείς να βάλουμε |x|. Για να απομονώσουμε το απόλυτο που θέλουμε θα ακολουθήσουμε τη γνωστή διαδικασία που ακολουθούμε σε όλες τις εξισώσεις α΄ βαθμού.
Πρώτα θα διώξουμε τους παρονομαστές πολλαπλασιάζοντας κάθε όρο με το Ε.Κ.Π. των παρονομαστών που είναι το 12
![]()
![]()
Τώρα διώχνουμε τις παρενθέσεις κάνοντας χρήση της επιμεριστικής ιδιότητας
![]()
Χωρίζουμε τους γνωστούς από τους άγνωστους ώστε να μπορέσουμε να συνεχίσουμε τις πράξεις χωρίς να ξεχνάμε ότι προς το παρόν άγνωστος είναι το |x| κι όχι το x
![]()
![]()
άρα
![]()
ή πιο απλά
![]()
Αφού καταφέραμε κι απομονώσαμε το απόλυτο μπορούμε σύμφωνα με όσα έχουμε πει πιο πάνω ν΄απαντήσουμε ότι ![]() ή
ή ![]()
[/gn_spoiler]
Άσκηση 2: Να λυθεί η εξίσωση 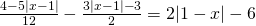
[gn_spoiler title=»Λύση:»]Όπως θα παρατηρήσατε η εξίσωση αυτή είναι ίδια με την προηγούμενη με την μόνη αλλαγή αντί για |x| έχουμε |x-1|. Και πάλι επειδή οι αριθμοί 1-x και x-1 είναι αντίθετοι η εξίσωση θα γίνει
![]()
και θα λυθεί με τον ίδιο ακριβώς τρόπο καταλήγοντας στο
![Rendered by QuickLaTeX.com \[|x-1|=2 \Leftrightarrow\left\{\begin{matrix}x-1=-2\Leftrightarrow x=-2+1=-1\\ \eta\\x-1=2\Leftrightarrow x=2+1=3\end{matrix}\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-3d8b31a9400dddc58f39cee2363a52b1_l3.png)
Έτσι λοιπόν βλέπουμε ότι αν τα απόλυτα που έχουμε στην εξίσωση περιέχουν ίσες ή ακόμη και αντίθετες παραστάσεις, τότε δεν μας ενδιαφέρει το περιεχόμενη της απόλυτης τιμής. Λύνουμε την εξίσωση κανονικά όπως όλες τις εξισώσεις «κουβαλώντας» το απόλυτο μέχρι να καταφέρουμε να το απομονώσουμε και στο τέλος το πετάμε (πάντα σύμφωνα με το διάγραμμα που έχουμε παραπάνω).
Επειδή κάποιοι μπορεί να «ψιλό» μπερδεύονται κουβαλώντας το απόλυτο μπορούν να γλυτώσουν από αυτό με την συνηθισμένη στα μαθηματικά μέθοδο: «αν κάτι μ΄ενοχλεί κάνω πως δεν το βλέπω». Έτσι λοιπόν θα μπορούσαμε να θέσουμε όπου |x-1|=α (σχέση 1) και να λύσουμε την εξίσωση χωρίς το απόλυτο. Μόλις ξεμπερδέψουμε με το α και το βρούμε γυρίζουμε και το αντικαθιστούμε στη σχέση 1 απ’ όπου υπολογίζουμε το x που μας ενδιαφέρει.
Watch me 
Θέτω |χ-1|=α (σχέση 1) οπότε η εξίσωση γίνεται
![]()
![]()
![]()
![]()
![]()
Ας μην ξεχνάμε όμως ότι δεν ψάχναμε το α αλλά το x. Πάμε λοιπόν στη σχέση 1 και αντικαθιστούμε όπου α=2, οπότε
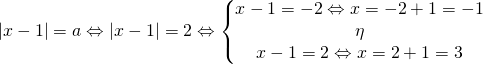
Τη μέθοδο αυτή για να είμαι ειλικρινής δεν σας την έδειξα μόνο για την περίπτωση που κάποιος δυσκολεύεται με τα πολλά απόλυτα αλλά και γιατί σε κάποιες περιπτώσεις θα έλεγα δεν μπορούμε να την αποφύγουμε γι’ αυτό καλό είναι να την ξέρουμε. Δείτε την επόμενη άσκηση και θα καταλάβετε. [/gn_spoiler]
Άσκηση 3: Να βρεθούν οι αριθμοί που ικανοποιούν τη σχέση 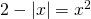
[gn_spoiler title=»Λύση:»] Την άσκηση αυτή θα μπορούσαμε να τη λύσουμε απομονώνοντας το απόλυτο στο ένα μέλος, οπότε η εξίσωση να γίνει |x|=2 – x2 αλλά πιστεύω ότι έτσι δεν θα μας συνέφερε γιατί το δεύτερο μέλος (το 2 – x2) δεν γνωρίζουμε αν είναι θετικός ή αρνητικός αριθμός ( για κάποιες τιμές του x γίνεται θετικός, για κάποιες αρνητικός και για κάποιες γίνεται ίσος με 0). Έτσι θα έπρεπε να διακρίνουμε περιπτώσεις και να πούμε
Περίπτωση 1η: αν το 2 – x2 είναι αρνητικό η εξίσωσή μας είναι αδύνατη (βλέπε και το σχεδιάγραμμα πιο πάνω)
Περίπτωση 2η: αν ![]() , τότε x=2-x2 ή x= – (2-x2 ) και να λύσω δύο εξισώσεις (δεύτερου βαθμού η καθεμία) κι αφού βρω τις λύσεις να κρατήσω από αυτές μόνο εκείνες που επαληθεύουν τον περιορισμό
, τότε x=2-x2 ή x= – (2-x2 ) και να λύσω δύο εξισώσεις (δεύτερου βαθμού η καθεμία) κι αφού βρω τις λύσεις να κρατήσω από αυτές μόνο εκείνες που επαληθεύουν τον περιορισμό ![]() .
.
Για να γλυτώσουμε όλη αυτή τη δουλειά μπορούμε να σκεφτούμε λίγο πιο έξυπνα και να αντικαταστήσουμε το |x| με έναν άλλο αριθμό έστω α. Τότε θα έχουμε γλυτώσει και από το |x| αλλά και από το x2 γιατί το x2=|x2|=|x|2=α2 (ρίξε μια ματιά στις ιδιότητες των απολύτων). Ας δούμε τώρα πως έχει καταντήσει η εξίσωσή μας θέτοντας |x|=α,
![]()
Η διακρίνουσα του τριωνύμου είναι
![]()
και οι λύσεις της εξίσωσης αυτής είναι
![]()
ή
![]()
Εύκολα λοιπόν βρήκαμε το α, το x όμως είναι αυτό που μας ενδιαφέρει
![Rendered by QuickLaTeX.com \[\left | x \right |=\alpha \Leftrightarrow \left\{\begin{matrix} \left | x \right |=1 \Leftrightarrow x=\pm 1\\\eta'\\ \left | x \right |=-2 & \alpha \delta \upsilon \nu \alpha \tau \eta \end{matrix}\right.\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-198fbd64d110d48053f6e400aa566f03_l3.png)
[/gn_spoiler]
Άσκηση 4: Να βρεθούν οι αριθμοί που ικανοποιούν τη σχέση 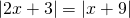
[gn_spoiler title=»Λύση:»] Στην άσκηση αυτή ανήκει στη γενική κατηγορία
![]()
και λύνεται με την ισοδυναμία
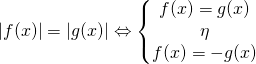
Έχουμε λοιπόν 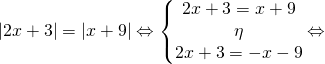
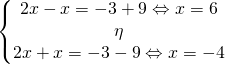 [/gn_spoiler]
[/gn_spoiler]
Μάθε τα όριά σου και … ξεπέρασέ τα !!!
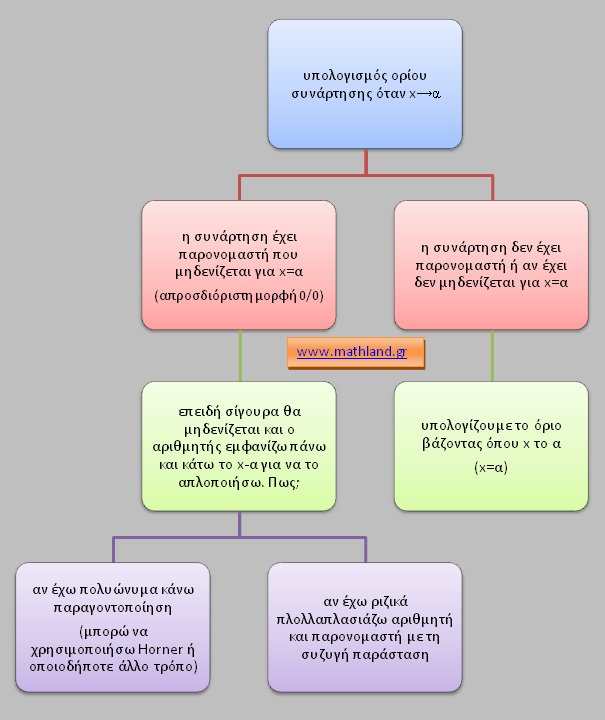
Πως μπορούμε να υπολογίζουμε το όριο μιας συνάρτησης όταν το χ τείνει σε πραγματικό αριθμό ακόμη και στην περίπτωση που μηδενίζεται ο παρονομαστής.
Γ΄ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
Εισαγωγή
Το πρώτο πράγμα που πρέπει να συζητήσουμε εδώ είναι το τι είναι το όριο μιας συνάρτησης. Δυστυχώς ή ευτυχώς στα μαθηματικά της γενικής παιδείας δεν μπορούμε να δώσουμε μαθηματικό ορισμό του ορίου, οπότε το μόνο που μας μένει είναι να πούμε «στο περίπου» τι είναι το όριο μιας συνάρτησης σε κάποιο συγκεκριμένο σημείο. Ας το δούμε αυτό καλύτερα με ένα παράδειγμα. Ας υποθέσουμε ότι έχουμε τη συνάρτηση f που έχει τύπο ![]() , το Πεδίο Ορισμού αυτής είναι το
, το Πεδίο Ορισμού αυτής είναι το ![]() (αν δεν θυμάσαι πως βρίσκουμε το Πεδίο Ορισμού μιας συνάρτησης κάνε κλικ εδώ). Στην περίπτωση που θέλουμε να βρούμε την τιμή που παίρνει f όταν το χ πάρει την τιμή 2 δεν έχουμε παρά να βρούμε το f(2) αντικαθιστώντας στον τύπο της f όπου x τον αριθμό 2 και βρίσκουμε
(αν δεν θυμάσαι πως βρίσκουμε το Πεδίο Ορισμού μιας συνάρτησης κάνε κλικ εδώ). Στην περίπτωση που θέλουμε να βρούμε την τιμή που παίρνει f όταν το χ πάρει την τιμή 2 δεν έχουμε παρά να βρούμε το f(2) αντικαθιστώντας στον τύπο της f όπου x τον αριθμό 2 και βρίσκουμε ![]() . Με αυτό τον απλό τρόπο μπορούμε να βρούμε την τιμή της f σε οποιοδήποτε σημείο του Πεδίου Oρισμού της. Αν θέλουμε όμως να δούμε τι τιμή παίρνει η συνάρτησή μας για x=1 αυτό είναι αδύνατο γιατί αφού το 1 δεν ανήκει στο Πεδίο Ορισμού της συνάρτησης δεν έχω το δικαίωμα να βάλω όπου χ το 1.
. Με αυτό τον απλό τρόπο μπορούμε να βρούμε την τιμή της f σε οποιοδήποτε σημείο του Πεδίου Oρισμού της. Αν θέλουμε όμως να δούμε τι τιμή παίρνει η συνάρτησή μας για x=1 αυτό είναι αδύνατο γιατί αφού το 1 δεν ανήκει στο Πεδίο Ορισμού της συνάρτησης δεν έχω το δικαίωμα να βάλω όπου χ το 1.
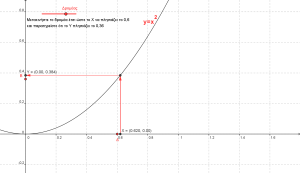
Το μόνο που μπορώ να κάνω είναι να δω το πως «συμπεριφέρεται» η συνάρτηση f όταν το x παίρνει τιμές πάρα πολύ κοντά στο 1. Σε αυτή τη περίπτωση λοιπόν αντί να βάζω x=1, χρησιμοποιώ την έννοια του «ορίου» και γράφω ![]() που σημαίνει ότι το x πλησιάζει (πάρα πολύ κοντά) στον αριθμό 1 και διαβάζεται «το x τείνει – πλησιάζει δηλαδή – το 1». Υποθέτουμε, προς το παρόν, ότι βρήκαμε το όριο και ότι αυτό είναι 2 ( θα δούμε παρακάτω πως υπολογίζεται ) δεν είναι σωστό να γράψουμε f(1)=2 γιατί αυτό σημαίνει ότι στη συνάρτηση f θέσαμε όπου x τον αριθμό 1 και αυτή μας έδωσε ως αποτέλεσμα την τιμή 2. Το σωστό είναι να γράψουμε
που σημαίνει ότι το x πλησιάζει (πάρα πολύ κοντά) στον αριθμό 1 και διαβάζεται «το x τείνει – πλησιάζει δηλαδή – το 1». Υποθέτουμε, προς το παρόν, ότι βρήκαμε το όριο και ότι αυτό είναι 2 ( θα δούμε παρακάτω πως υπολογίζεται ) δεν είναι σωστό να γράψουμε f(1)=2 γιατί αυτό σημαίνει ότι στη συνάρτηση f θέσαμε όπου x τον αριθμό 1 και αυτή μας έδωσε ως αποτέλεσμα την τιμή 2. Το σωστό είναι να γράψουμε ![]() που διαβάζεται «το όριο της συνάρτησης f , όταν το x τείνει στο 1, είναι ο αριθμός 2» και σημαίνει ότι: όταν το x παίρνει τιμές πολύ κοντά στο 1 το f(x) παίρνει τιμές πολύ κοντά στο 2. Επειδή σκοπός του άρθρου αυτού δεν είναι η έννοια του ορίου αλλά ο τρόπος υπολογισμού του ας προχωρήσουμε στο πως μπορούμε να βρούμε το όριο μιας συνάρτησης f όταν το x τείνει σε κάποιον αριθμό a (
που διαβάζεται «το όριο της συνάρτησης f , όταν το x τείνει στο 1, είναι ο αριθμός 2» και σημαίνει ότι: όταν το x παίρνει τιμές πολύ κοντά στο 1 το f(x) παίρνει τιμές πολύ κοντά στο 2. Επειδή σκοπός του άρθρου αυτού δεν είναι η έννοια του ορίου αλλά ο τρόπος υπολογισμού του ας προχωρήσουμε στο πως μπορούμε να βρούμε το όριο μιας συνάρτησης f όταν το x τείνει σε κάποιον αριθμό a (![]() ) και με την προϋπόθεση ότι το x θα μπορεί να πλησιάζει τον αριθμό a. Γιατί δεν μπορούμε να μιλάμε για όριο μιας συνάρτησης έστω g στο 5 αν το Πεδίο Ορισμού της είναι για παράδειγμα το σύνολο
) και με την προϋπόθεση ότι το x θα μπορεί να πλησιάζει τον αριθμό a. Γιατί δεν μπορούμε να μιλάμε για όριο μιας συνάρτησης έστω g στο 5 αν το Πεδίο Ορισμού της είναι για παράδειγμα το σύνολο ![]() αφού το x ανήκει σε αυτό το διάστημα μπορεί να πάρει οποιαδήποτε τιμή μεγαλύτερη του 1 αλλά μικρότερη του 4 πως λοιπόν θα του δώσουμε τιμές κοντά στο 5;
αφού το x ανήκει σε αυτό το διάστημα μπορεί να πάρει οποιαδήποτε τιμή μεγαλύτερη του 1 αλλά μικρότερη του 4 πως λοιπόν θα του δώσουμε τιμές κοντά στο 5;
Υπολογισμός Ορίου
[su_tabs style=1]
[su_tab title=»Η απλή περίπτωση»]
Στην περίπτωση που θέλουμε να υπολογίσουμε το όριο μιας συνάρτησης f όταν το x τείνει σε κάποιο σημείο a , τότε πολύ απλά βρίσκουμε το f(a) αντικαθιστώντας όπου x τον αριθμό a αρκεί:
- να μπορεί, όπως αναφέραμε πιο πάνω, το x να πλησιάζει το a , και
- να μην μηδενίζεται ο παρονομαστής της συνάρτησης
Ας δούμε κάποια παραδείγματα:
- Δίνεται η συνάρτηση
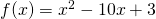 , να βρεθεί το
, να βρεθεί το  .Λύση: Βλέπουμε ότι η f έχει Πεδίο Ορισμού όλο το
.Λύση: Βλέπουμε ότι η f έχει Πεδίο Ορισμού όλο το 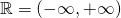 κι επομένως το x μπορεί να πλησιάζει στο 1 οπότε μπορούμε να ξεκινήσουμε τον υπολογισμό του ορίου:
κι επομένως το x μπορεί να πλησιάζει στο 1 οπότε μπορούμε να ξεκινήσουμε τον υπολογισμό του ορίου:
![Rendered by QuickLaTeX.com \[\underset{x\to 1 }{\mathop{\lim }}f(x)=\underset{x\to 1 }{\mathop{\lim }}(x^2-10x+3)=\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-613079e2fff0e19ef903d2209ed2b52a_l3.png)
![Rendered by QuickLaTeX.com \[=1^2-10\cdot 1+3=-6\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-1f401510464e4007779dd36248abe20b_l3.png)
- Για τη συνάρτηση
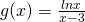 να βρείτε τα όρια
να βρείτε τα όρια 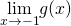 και
και 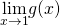 .Λύση: Το πρώτο πράγμα που κάνουμε πάντα είτε το ζητάει η άσκηση είτε όχι είναι να βρούμε το πεδίο ορισμού της συνάρτησης η οποία παρατηρούμε ότι έχει έχει λογάριθμο και πρέπει το περιεχόμενό του να είναι θετικό (άρα πρέπει x>0) και παρονομαστή το x-3 που δεν πρέπει να μηδενίζεται κι επομένως το x δεν μπορεί να πάρει την τιμή 3 καταλήγουμε λοιπόν στο ότι το πεδίο ορισμού της g είναι το
.Λύση: Το πρώτο πράγμα που κάνουμε πάντα είτε το ζητάει η άσκηση είτε όχι είναι να βρούμε το πεδίο ορισμού της συνάρτησης η οποία παρατηρούμε ότι έχει έχει λογάριθμο και πρέπει το περιεχόμενό του να είναι θετικό (άρα πρέπει x>0) και παρονομαστή το x-3 που δεν πρέπει να μηδενίζεται κι επομένως το x δεν μπορεί να πάρει την τιμή 3 καταλήγουμε λοιπόν στο ότι το πεδίο ορισμού της g είναι το 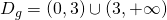 . Όσον αφορά στα όρια τώρα, βλέπουμε ότι το πρώτο από αυτά δεν έχει νόημα αφού το x δεν έχει τη δυνατότητα να «πλησιάζει» το -1 οπότε το αφήνουμε και για να είμαι ειλικρινής δεν πιστεύω ότι θα ζητηθεί ποτέ κάτι τέτοιο. Πάμε τώρα στο δεύτερο όριο το οποίο και θα υπολογίσουμε κανονικότατα
. Όσον αφορά στα όρια τώρα, βλέπουμε ότι το πρώτο από αυτά δεν έχει νόημα αφού το x δεν έχει τη δυνατότητα να «πλησιάζει» το -1 οπότε το αφήνουμε και για να είμαι ειλικρινής δεν πιστεύω ότι θα ζητηθεί ποτέ κάτι τέτοιο. Πάμε τώρα στο δεύτερο όριο το οποίο και θα υπολογίσουμε κανονικότατα
![Rendered by QuickLaTeX.com \[\underset{x\to 1}{\mathop{\lim }}g(x)=\underset{x\to 1}{\mathop{\lim }}\frac{lnx}{x-3}=\frac{ln1}{1-3}=\frac{0}{-2}=0\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-30e6878e453519c0892787595321274b_l3.png)
- Να βρεθεί το όριο
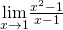
Λύση: Η συνάρτηση της οποίας αναζητάμε το όριο στο 1 είναι η![Rendered by QuickLaTeX.com \[h(x)=\frac{x^2-1}{x-1}\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-ca2eac187f9324a9f90db66551170ff2_l3.png)
. Επειδή η συνάρτηση έχει παρονομαστή το x-1 έχει πεδίο ορισμού το
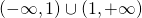 . Παρατηρούμε ότι το 1 δεν ανήκει στο πεδίο ορισμού της συνάρτησης, πράγμα που σημαίνει ότι δεν μπορώ να θέσω x=1, αυτό όμως δεν αποτελεί πρόβλημα αφού το x
. Παρατηρούμε ότι το 1 δεν ανήκει στο πεδίο ορισμού της συνάρτησης, πράγμα που σημαίνει ότι δεν μπορώ να θέσω x=1, αυτό όμως δεν αποτελεί πρόβλημα αφού το x έχει τη δυνατότητα να «προσεγγίσει» το 1 (δηλαδή μπορεί
έχει τη δυνατότητα να «προσεγγίσει» το 1 (δηλαδή μπορεί 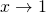 ) κι επομένως θα μπορούσαμε να υπολογίσουμε το όριο αυτό αν δεν είχαμε άλλο πρόβλημα. Και ποιο είναι το πρόβλημα αυτό; Ότι ο αριθμός 1 μηδενίζει τον παρονομαστή μας. Ευτυχώς όμως το 1 μηδενίζει και τον αριθμητή ( το x2-1 ) και αυτό μας λύνει τα χέρια γιατί σημαίνει ότι ο αριθμός 1 είναι ρίζα και του παρονομαστή αλλά και του αριθμητή κι όπως μάθαμε στη Β΄ Λυκείου, στον αριθμητή x2-1 είναι κρυμμένος ο παράγοντας x-1 [wpspoiler name=»διαβάστε εδώ το γιατί» ]όταν ένα πολυώνυμο p(x) μηδενίζεται για x=ρ, τότε θα έχει ρίζα τον αριθμό ρ και συνεπώς θα έχει παράγοντα το x-ρ, πράγμα που σημαίνει ότι το πολυώνυμο αναλύεται σε γινόμενο παραγόντων όπου ο ένας από τους παράγοντές του θα είναι το x-ρ, δηλαδή θα ισχύει p(x)=(x – ρ).π(x) , άρα:
) κι επομένως θα μπορούσαμε να υπολογίσουμε το όριο αυτό αν δεν είχαμε άλλο πρόβλημα. Και ποιο είναι το πρόβλημα αυτό; Ότι ο αριθμός 1 μηδενίζει τον παρονομαστή μας. Ευτυχώς όμως το 1 μηδενίζει και τον αριθμητή ( το x2-1 ) και αυτό μας λύνει τα χέρια γιατί σημαίνει ότι ο αριθμός 1 είναι ρίζα και του παρονομαστή αλλά και του αριθμητή κι όπως μάθαμε στη Β΄ Λυκείου, στον αριθμητή x2-1 είναι κρυμμένος ο παράγοντας x-1 [wpspoiler name=»διαβάστε εδώ το γιατί» ]όταν ένα πολυώνυμο p(x) μηδενίζεται για x=ρ, τότε θα έχει ρίζα τον αριθμό ρ και συνεπώς θα έχει παράγοντα το x-ρ, πράγμα που σημαίνει ότι το πολυώνυμο αναλύεται σε γινόμενο παραγόντων όπου ο ένας από τους παράγοντές του θα είναι το x-ρ, δηλαδή θα ισχύει p(x)=(x – ρ).π(x) , άρα:
![Rendered by QuickLaTeX.com \[P(\rho)=0 \Leftrightarrow P(x)=(x-\rho) \cdot \pi(x)\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-11d9992d557a8f258d8c87b25852e922_l3.png)
[/wpspoiler] Έτσι εμείς αρκεί να τον εμφανίσουμε για να μπορέσουμε να τον εξαφανίσουμε (δηλαδή να τον απλοποιήσουμε) κι αυτό δεν είναι δύσκολο αφού είναι γνωστό ότι ισχύει x2-1=(x-1)(x+1). Ας δούμε τώρα πως θα υπολογιστεί το όριο
![Rendered by QuickLaTeX.com \[\underset{x\to 1}{\mathop{\lim }}\frac{x^2-1}{x-1}=\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-bcf0e1e17ac10cdd32b676e9754fe378_l3.png)
![Rendered by QuickLaTeX.com \[\underset{x\to 1}{\mathop{\lim }}\frac{(x-1)(x+1)}{x-1}=\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-ec82cca5e5e1ff459930ec82764e430e_l3.png)
![Rendered by QuickLaTeX.com \[\underset{x\to 1}{\mathop{\lim }},(x+1)=1+1=2\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-b7bbf83af6d4f476d03c9afdc66283fd_l3.png)
Το παράδειγμα αυτό που λύσαμε ανήκει στην πιο συνηθισμένη κατηγορία ορίων που θα συναντήσετε φέτος και είναι αναγκαίο να επεκταθούμε κι άλλο γι’ αυτό το λόγο κάντε κλικ εδώ και μετά στην καρτέλα «Η Απροσδιόριστη μορφή 0/0» που βρίσκεται λίγο παραπάνω.[/su_tab]
[su_tab title=»Η απροσδιόριστη μορφή 0/0″]
Κατά την αναζήτηση του ορίου μιας κλασματικής συνάρτησης ας την πούμε f σε σημείο α ( ![]() )είναι πιθανό να μηδενίζεται για x=α ο αριθμητής και ο παρονομαστής της συνάρτησης. Σε μια τέτοια περίπτωση ( που ονομάζεται απροσδιόριστη μορφή 0/0) δεν μπορούμε να υπολογίσουμε το όριο από τη συνάρτηση που μας έχουν δώσει κι έτσι καταφεύγουμε στο να υπολογίσουμε το όριο αφού πρώτα απλοποιήσουμε την f . Το πως το καταφέρνουμε αυτό εξαρτάται από τη συνάρτηση που μας έχει δοθεί και θα το δούμε σε παραδείγματα παρακάτω. Η βασική ιδέα όμως είναι κοινή και απλή:
)είναι πιθανό να μηδενίζεται για x=α ο αριθμητής και ο παρονομαστής της συνάρτησης. Σε μια τέτοια περίπτωση ( που ονομάζεται απροσδιόριστη μορφή 0/0) δεν μπορούμε να υπολογίσουμε το όριο από τη συνάρτηση που μας έχουν δώσει κι έτσι καταφεύγουμε στο να υπολογίσουμε το όριο αφού πρώτα απλοποιήσουμε την f . Το πως το καταφέρνουμε αυτό εξαρτάται από τη συνάρτηση που μας έχει δοθεί και θα το δούμε σε παραδείγματα παρακάτω. Η βασική ιδέα όμως είναι κοινή και απλή:
από τη στιγμή που βλέπουμε ότι αν θέσουμε x=α στη συνάρτηση μηδενίζεται ο αριθμητής της και ο παρονομαστής της είμαστε σίγουροι ότι και στον αριθμητή αλλά και στον παρονομαστή είναι «κρυμμένος» ο παράγοντας x-α. Σκοπός είναι να τον «εμφανίσουμε» πάνω και κάτω στο κλάσμα έτσι ώστε να τον απλοποιήσουμε (να τον «εξαφανίσουμε» γιατί αυτός ευθύνεται για το 0/0). Μετά την απλοποίηση αυτή είμαστε σε θέση να υπολογίσουμε πολύ απλά το όριο αντικαθιστώντας όπου x το α.
Για να δούμε όμως αναλυτικά πως θα εμφανίσουμε το x-α θα χωρίσουμε τη διαδικασία σε δύο περιπτώσεις. Στην περίπτωση που οι όροι του κλάσματος είναι πολυώνυμα και στην περίπτωση που στο κλάσμα έχουμε τετραγωνική ρίζα. Κάντε κλικ στις παρακάτω μπάρες να δείτε λυμένα βασικά παραδείγματα με την απαραίτητη μεθοδολογία
[wpspoiler name=»Πολυώνυμα»]
Δίνεται η συνάρτηση ![]() . Να βρεθεί το όριο
. Να βρεθεί το όριο ![]() .
.
Λύση: Παρατηρούμε ότι ο παρονομαστής για x=1 μηδενίζεται (2.12-2=2-2=0). Είμαστε σίγουροι ότι και ο αριθμητής μηδενίζεται για x=1 αλλά το τσεκάρουμε (13-12+1-1=0). Τώρα κάνουμε γινόμενο τον αριθμητή και τον παρονομαστή (μπορείτε να θυμηθείτε την παραγοντοποίηση εδώ):
x3-x2+x-1=(x3-x2)+(x-1)[ref] κάναμε ομαδοποίηση[/ref]=x2(x-1)+(x-1)=(x-1)(x2+1). Βλέπουμε ότι εμφανίστηκε το x-1 άρα είμαστε εντάξει
2x2-2=2(x2-1)=2(x-1)(x+1)[ref]κοινός παράγοντας και διαφορά τετραγώνων[/ref] κι εδώ εντάξει, οπότε:
![]()
επομένως
![]()
Όπως βλέπουμε αν έχουμε υπόψη μας τι ακριβώς θέλουμε (να εμφανίσουμε τον παράγοντα x-1 και να τον απλοποιήσουμε) ο υπολογισμός ενός ορίου είναι εύκολη υπόθεση. Κι επειδή το μάθημα αυτό αφορά και μαθητές θεωρητικής κατεύθυνσης που ίσως αντιμετωπίζουν κάποιες δυσκολίες στην παραγοντοποίηση θα σας προτείνω κι έναν άλλο τρόπο που θεωρώ ευκολότερο και ίσως πιο σύντομο, το σχήμα Horner που διδαχθήκαμε στη Β΄τάξη του Λυκείου. Ας δούμε λοιπόν την ίδια άσκηση λυμένη με αυτή τη μέθοδο:
Για να κάνω γινόμενο τον αριθμητή x3-x2+x-1 κάνω σχήμα Horner με τον αριθμό 1
| 1 | -1 | 1 | -1 | 1 |
| 1 | 0 | 1 | ||
| 1 | 0 | 1 | 0 |
Η γαλάζια περιοχή περιέχει τους συντελεστές του πολυωνύμου x3-x2+x-1 που θέλω να κάνω γινόμενο
Η πορτοκαλί περιοχή θα έχει πάντα τον αριθμό στον οποίο τείνει το x (εδώ είναι το 1)
Η ροζ περιοχή θα είναι πάντα 0
Η πράσινη περιοχή μας δίνει τους συντελεστές του πολυωνύμου που θα μείνει όταν απλοποιηθεί το «ενοχλητικό» x-1. Έτσι η νέα μας συνάρτηση θα έχει αριθμητή τον x2+1 αφού το από το σχήμα Horner προκύπτει ότι x3-x2+x-1=(x-1)(x2+1) και το x-1 θα απλοποιηθεί.
Με την ίδια διαδικασία βρίσκω τον νέο παρονομαστή της συνάρτησης
| 2 | 0 | -2 | 1 |
| 2 | 2 | ||
| 2 | 2 | 0 |
οπότε ο παρονομαστής 2x2-2(το γαλάζιο) θα γίνει 2x+2(το πράσινο), αφού από το σχήμα Horner προκύπτει 2x2-2=(x-1)(2x+2) και το x-1 θα απλοποιηθεί.
Τελικά η συνάρτηση f θα γίνει
![]()
κι επομένως το όριο είναι
![]()
Το να ξεφύγεις από την απροσδιόριστη μορφή 0/0 στην περίπτωση που στη συνάρτηση έχεις πολυώνυμο το σχήμα Horner είναι το πιο εύκολο. Το δύσκολο είναι να το περιγράψω πλήρως μέσα από αυτό το άρθρο γι’ αυτό αν κάπου σας μπέρδεψα ζητήστε από τον καθηγητή σας να σας το θυμίσει (είναι υπόθεση δύο λεπτών) ή στείλτε μου μήνυμα να λύσουμε ότι απορία έχετε. Καλού κακού όμως θα λύσουμε ένα παράδειγμα ακόμη:
Να βρεθεί το ![]() .
.
Λύση: Για x=2 μηδενίζονται παρονομαστής και αριθμητής άρα πρέπει να εξαλειφθεί ο παράγοντας x-2.
Στον παρονομαστή υπάρχει το x-2 άρα δεν χρειάζεται να κάνουμε κάτι.
Στον αριθμητή θα κάνουμε σχήμα Horner με το 2 γιατί το x τείνει στο 2,
| 2 | -3 | -2 | 2 |
| 4 | 2 | ||
| 2 | 1 | 0 |
οπότε 2x2-3x-2=(x-2)(2x+1) άρα
![]()
![]()
![]()
[wpspoiler name=»Ριζικά»]
- Για να ξεφύγω από το 0/0 όταν το x τείνει στο α, πρέπει να «εμφανίσω» και μετά να «εξαφανίσω» το x-α από αριθμητή & παρονομαστή
Έστω ότι έχουμε τη συνάρτηση ![]() και θέλουμε να βρούμε το όριο της όταν το τείνει στο 5. Παρατηρούμε ότι για x=5 μηδενίζονται παρονομαστής και αριθμητής, πράγμα που σημαίνει ότι έχω απροσδιόριστη μορφή 0/0, και σύμφωνα με τα όσα έχουμε πει μέχρι τώρα στον αριθμητή αλλά και στον παρονομαστή της συνάρτησης υπάρχει ο παράγοντας x-5 ο οποίος ευθύνεται για τα μηδενικά. Εγώ πρέπει λοιπόν να τον «εμφανίσω» για να τον «εξαφανίσω» . Ευτυχώς στο παράδειγμά μας θα πρέπει να ασχοληθούμε μόνο με τον αριθμητή αφού στον παρονομαστή υπάρχει το x-5 και δεν χρειάζεται να κάνω κάτι. Ο αριθμητής όμως δεν είναι πολυώνυμο για να χρησιμοποιήσω σχήμα Horner ή έστω τους κανόνες της παραγοντοποίησης που έχουμε μάθει μέχρι τώρα. Υπάρχουν αρκετά «κόλπα» για να καταφέρουμε αυτό που θέλουμε αλλά θα αναφερθώ πρώτα στο πιο συνηθισμένο:
και θέλουμε να βρούμε το όριο της όταν το τείνει στο 5. Παρατηρούμε ότι για x=5 μηδενίζονται παρονομαστής και αριθμητής, πράγμα που σημαίνει ότι έχω απροσδιόριστη μορφή 0/0, και σύμφωνα με τα όσα έχουμε πει μέχρι τώρα στον αριθμητή αλλά και στον παρονομαστή της συνάρτησης υπάρχει ο παράγοντας x-5 ο οποίος ευθύνεται για τα μηδενικά. Εγώ πρέπει λοιπόν να τον «εμφανίσω» για να τον «εξαφανίσω» . Ευτυχώς στο παράδειγμά μας θα πρέπει να ασχοληθούμε μόνο με τον αριθμητή αφού στον παρονομαστή υπάρχει το x-5 και δεν χρειάζεται να κάνω κάτι. Ο αριθμητής όμως δεν είναι πολυώνυμο για να χρησιμοποιήσω σχήμα Horner ή έστω τους κανόνες της παραγοντοποίησης που έχουμε μάθει μέχρι τώρα. Υπάρχουν αρκετά «κόλπα» για να καταφέρουμε αυτό που θέλουμε αλλά θα αναφερθώ πρώτα στο πιο συνηθισμένο:
Κάνουμε χρήση της γνωστής ταυτότητας «διαφορά τετραγώνων». Ας την θυμηθούμε ![]() . Την ταυτότητα αυτή μπορούμε να την χρησιμοποιήσουμε και με αυτές τις μορφές:
. Την ταυτότητα αυτή μπορούμε να την χρησιμοποιήσουμε και με αυτές τις μορφές:
-
![Rendered by QuickLaTeX.com \[(\sqrt{A}-\sqrt{B})(\sqrt{A}+\sqrt{B})=(\sqrt{A})^2-(\sqrt{B})^2\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-14df396e773f6dfd4a5fce0934ba0cea_l3.png)
ή ακόμη καλύτερα
![Rendered by QuickLaTeX.com \[(\sqrt{A}-\sqrt{B})(\sqrt{A}+\sqrt{B})=A-B\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-dce0e83c3fbe2e70ad3bd1364a7b6354_l3.png)
-
![Rendered by QuickLaTeX.com \[(\sqrt{A}-B)(\sqrt{A}+B)=A-B^2\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-890c6d5e3b4b35cd7ded4730b24710c4_l3.png)
-
![Rendered by QuickLaTeX.com \[(A-\sqrt{B})(A+\sqrt{B})=A^2-B\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-2370eae11a90ffd7df8a13628462b01e_l3.png)
Για να δούμε τώρα τι κερδίζουμε από αυτό; Όταν θα μας τυχαίνει μία από τις παραστάσεις που βρίσκονται στις παραπάνω παρενθέσεις εμείς θα πολλαπλασιάζουμε αριθμητή αλλά και παρονομαστή με την διπλανή παρένθεση (λέγεται «συζυγής παράσταση» π.χ. η συζυγής παράσταση της ![]() είναι η
είναι η ![]() ) ώστε σύμφωνα με την ταυτότητα να φύγουν οι ρίζες. Ας το δούμε όμως στη πράξη, στη συνάρτηση f έχω την παράσταση
) ώστε σύμφωνα με την ταυτότητα να φύγουν οι ρίζες. Ας το δούμε όμως στη πράξη, στη συνάρτηση f έχω την παράσταση ![]() η συζυγής παράσταση αυτής είναι η
η συζυγής παράσταση αυτής είναι η ![]() πολλαπλασιάζω λοιπόν αριθμητή και παρονομαστή με αυτή
πολλαπλασιάζω λοιπόν αριθμητή και παρονομαστή με αυτή
![]()
![]()
![]()
![]()
οπότε αφού καταφέραμε και διώξαμε το x-5 μπορούμε να υπολογίσουμε το όριο
![]()
Ένα παράδειγμα ακόμη για να το καταλάβουμε καλύτερα. Να βρεθεί το ![]()
Λύση: Βάζοντας όπου h το 0 παίρνουμε 0/0. Φταίει ο παράγοντας h-0, δηλαδή το h. Κάτω το βλέπουμε και δεν κάνουμε τίποτα. Πάνω έχουμε ![]() η συζυγής της είναι η
η συζυγής της είναι η ![]() με την οποία πολλαπλασιάζω πάνω και κάτω και παίρνω
με την οποία πολλαπλασιάζω πάνω και κάτω και παίρνω
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Κι εδώ τελειώνουν οι περιπτώσεις υπολογισμού ορίων που μπορεί να συναντήσει ένας μαθητής Γ΄Λυκείου στα Μαθηματικά της Γενικής Παιδείας (για την κατεύθυνση έχουμε πολλά να πούμε ακόμη). Καταλαβαίνω ότι το άρθρο είναι τεράστιο, θα μπορούσε να είχε γίνει τριλογία, αλλά θεώρησα καλύτερο να υπάρχουν όλες οι περιπτώσεις μαζί για να έχετε μια ολοκληρωμένη εικόνα. Προτείνω να το διαβάσετε περισσότερες από μία φορά και εξασκηθείτε με τις ασκήσεις που σας δίνω στο παρακάτω link.[/wpspoiler]
Επιστροφή^^^
[/su_tab]
[/su_tabs]
[wpspoiler name=»Δείτε την μεθοδολογία» style=»wpui-quark»]
[/wpspoiler]
Θέλω να μάθω…πως βρίσκουμε το Πεδίο Ορισμού μιας συνάρτησης
Τι είναι το Πεδίο Ορισμού μιας συνάρτησης; Πως το υπολογίζω και γιατί;
Γ ‘ ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ & ΚΑΤΕΥΘΥΝΣΗΣ
Ας φανταστούμε τη συνάρτηση σαν μια “προξενήτρα” μιας και η δουλειά της είναι να “ζευγαρώνει” αριθμούς. Πάρτε για παράδειγμα τη συνάρτηση ![]() η οποία παίρνει τον αριθμό x και τον παντρεύει με τον αριθμό 2x, ζευγαρώνει δηλαδή κάθε αριθμό με τον διπλάσιό του, έτσι δημιουργεί ζεύγη αριθμών όπως το (1,2) αφού για χ=1, δίνει f(1)=2, το (3,6) αφού για χ=3 έχουμε f(3)=6. Η συγκεκριμένη συνάρτηση μπορεί να ζευγαρώσει οποιοδήποτε αριθμό και να της ζητήσουμε. Υπάρχουν όμως συναρτήσεις που δεν μπορούν να το κάνουν αυτό σε όλους τους αριθμούς, έχουν δηλαδή κάποιους περιορισμούς. Ας δούμε για παράδειγμα την
η οποία παίρνει τον αριθμό x και τον παντρεύει με τον αριθμό 2x, ζευγαρώνει δηλαδή κάθε αριθμό με τον διπλάσιό του, έτσι δημιουργεί ζεύγη αριθμών όπως το (1,2) αφού για χ=1, δίνει f(1)=2, το (3,6) αφού για χ=3 έχουμε f(3)=6. Η συγκεκριμένη συνάρτηση μπορεί να ζευγαρώσει οποιοδήποτε αριθμό και να της ζητήσουμε. Υπάρχουν όμως συναρτήσεις που δεν μπορούν να το κάνουν αυτό σε όλους τους αριθμούς, έχουν δηλαδή κάποιους περιορισμούς. Ας δούμε για παράδειγμα την ![]() η οποία “παντρεύει” έναν αριθμό με τον αντίστροφό του, δηλαδή το 5 με το 1/5 αφού g(5)=1/5, το 3/5 με το 5/3 γιατί g(3/5)=5/3 κ.τ.λ.. Το μοναδικό αριθμό όμως που δεν μπορεί να ταιριάξει είναι το 0 γιατί όπως έχουμε μάθει από το Γυμνάσιο ήδη το 0 δεν έχει αντίστροφο (για να μην αναφέρω και το Δημοτικό που μάθαμε ότι δεν ορίζεται διαίρεση με το 0). Όταν λοιπόν μας δίνουν τον τύπο μιας συνάρτησης το πρώτο πράγμα που πρέπει να κάνουμε πριν καν ξεκινήσουμε να την βάλουμε να δουλέψει είναι να βρούμε για ποιούς αριθμούς μπορεί να δουλέψει και για ποιούς όχι. Δεν δίνουμε στη συνάρτηση αριθμούς να παντρέψει χωρίς να δούμε πρώτα αν επιτρέπεται ένας τέτοιος γάμος γιατί υπάρχει περίπτωση αυτός ο γάμος να γεννήσει “τέρατα”. Έτσι λοιπόν όταν μιλάμε για Πεδίο Ορισμού μιας συνάρτησης στη πραγματικότητα εννοούμε το σύνολο των αριθμών που η συνάρτηση μπορεί να πάρει και να τους βρει σύντροφο. Και για να γίνουμε λίγο πιο τυπικοί Πεδίο Ορισμού μιας συνάρτησης f είναι το σύνολο των αριθμών x για τους οποίους υπάρχει το f(x).
η οποία “παντρεύει” έναν αριθμό με τον αντίστροφό του, δηλαδή το 5 με το 1/5 αφού g(5)=1/5, το 3/5 με το 5/3 γιατί g(3/5)=5/3 κ.τ.λ.. Το μοναδικό αριθμό όμως που δεν μπορεί να ταιριάξει είναι το 0 γιατί όπως έχουμε μάθει από το Γυμνάσιο ήδη το 0 δεν έχει αντίστροφο (για να μην αναφέρω και το Δημοτικό που μάθαμε ότι δεν ορίζεται διαίρεση με το 0). Όταν λοιπόν μας δίνουν τον τύπο μιας συνάρτησης το πρώτο πράγμα που πρέπει να κάνουμε πριν καν ξεκινήσουμε να την βάλουμε να δουλέψει είναι να βρούμε για ποιούς αριθμούς μπορεί να δουλέψει και για ποιούς όχι. Δεν δίνουμε στη συνάρτηση αριθμούς να παντρέψει χωρίς να δούμε πρώτα αν επιτρέπεται ένας τέτοιος γάμος γιατί υπάρχει περίπτωση αυτός ο γάμος να γεννήσει “τέρατα”. Έτσι λοιπόν όταν μιλάμε για Πεδίο Ορισμού μιας συνάρτησης στη πραγματικότητα εννοούμε το σύνολο των αριθμών που η συνάρτηση μπορεί να πάρει και να τους βρει σύντροφο. Και για να γίνουμε λίγο πιο τυπικοί Πεδίο Ορισμού μιας συνάρτησης f είναι το σύνολο των αριθμών x για τους οποίους υπάρχει το f(x).
Πως όμως μπορούμε να βρούμε το Πεδίο Ορισμού μιας συνάρτησης;
Αυτό είναι αρκετά απλό θα έλεγα αρκεί να ξέρουμε να λύνουμε εξισώσεις, ανισώσεις και να γνωρίζουμε ποιοί είναι οι
περιορισμοί που προκύπτουν από τον τύπο της συνάρτησης που μας έχει δοθεί. Το να γνωρίζουμε να λύνουμε εξισώσεις και ανισώσεις θα το θεωρήσουμε δεδομένο και θα σταθούμε λίγο στο ποιοι είναι οι περιορισμοί που έχουμε μάθει μέχρι τώρα.
Έτσι λοιπόν όταν μας δοθεί συνάρτηση που να έχει στον παρονομαστή της μεταβλητή (αυτές οι συναρτήσεις λέγονται ρητές) θα πρέπει εμείς να εξαιρέσουμε εκείνους τους αριθμούς που μηδενίζουν τον παρονομαστή της συνάρτησης.
Π.χ.1 Η συνάρτηση ![]() έχει παρονομαστή το 2x-4 πρέπει να δούμε για ποιές τιμές του x μηδενίζεται και να τις εξαιρέσουμε. Για το λόγο αυτό λύνουμε την εξίσωση
έχει παρονομαστή το 2x-4 πρέπει να δούμε για ποιές τιμές του x μηδενίζεται και να τις εξαιρέσουμε. Για το λόγο αυτό λύνουμε την εξίσωση
![]()
και απαντάμε ότι η συγκεκριμένη συνάρτηση έχει Πεδίο Ορισμού όλους τους (πραγματικούς) αριθμούς εκτός από τον αριθμό 2. Πιο καλά είναι να γράφουμε τον τύπο της συνάρτησης και δίπλα τον περιορισμό, δηλαδή ![]() με
με ![]() . Ή ακόμη καλύτερα
. Ή ακόμη καλύτερα ![]() , όπου με Df έχουμε συμβολίσει το Πεδίο Ορισμού της συνάρτησης f. Χρήσιμο είναι όπως θα δείτε αργότερα, όταν θα χρειαστεί να “μελετήσετε” τι ακριβώς δουλειά κάνει η συνάρτηση, να έχετε το Πεδίο Ορισμού σε μορφή διαστημάτων, έτσι σε αυτή τη περίπτωση θα μπορούσαμε να γράψουμε το αποτέλεσμα και ως εξής,
, όπου με Df έχουμε συμβολίσει το Πεδίο Ορισμού της συνάρτησης f. Χρήσιμο είναι όπως θα δείτε αργότερα, όταν θα χρειαστεί να “μελετήσετε” τι ακριβώς δουλειά κάνει η συνάρτηση, να έχετε το Πεδίο Ορισμού σε μορφή διαστημάτων, έτσι σε αυτή τη περίπτωση θα μπορούσαμε να γράψουμε το αποτέλεσμα και ως εξής, ![]() .
.
Π.χ.2 Η συνάρτηση ![]() έχει παρονομαστές τις παραστάσεις:
έχει παρονομαστές τις παραστάσεις:
x+1 η οποία μηδενίζεται για x= –1
(![]() ) και
) και
x2-5x+6 η οποία μηδενίζεται για x=2 ή για x=3
(x2-5x+6=0, Δ=β2-4αγ=1 και ![]() άρα x=2 ή x=3)
άρα x=2 ή x=3)
Η συνάρτηση g λοιπόν δεν μπορεί να δεχτεί στη θέση του x τους αριθμούς {-1,2,3} έτσι λέμε ότι το Πεδίο Ορισμού της είναι όλοι οι πραγματικοί αριθμοί εκτός από αυτούς και γράφουμε ![]() ή
ή![]() .
.
Τελικά καταλήγουμε στο ότι:
[su_box type=»info» title=»Tip 1″ color=»#0000FF»] όταν θέλουμε να βρούμε το πεδίο ορισμού μιας ρητής συνάρτησης της μορφής ![]() λύνουμε την εξίσωση g(x)=0 και γράφουμε Df=R-{οι λύσεις της εξίσωσης g(x)=0}[/su_box]
λύνουμε την εξίσωση g(x)=0 και γράφουμε Df=R-{οι λύσεις της εξίσωσης g(x)=0}[/su_box]
Αν ο τύπος της συνάρτησης που μας έχει δοθεί περιέχει ριζικά που το υπόρριζο (υπόρριζο είναι η παράσταση που βρίσκεται κάτω από το ριζικό) περιέχει μεταβλητή (τέτοιες συναρτήσεις λέγονται άρρητες), τότε απαιτούμε το υπόρριζο να είναι μεγαλύτερο ή ίσο με το 0.
π.χ.1 Η συνάρτηση ![]() ανήκει σε αυτή τη κατηγορία αφού στον τύπο της εμφανίζεται μια τουλάχιστον (τετραγωνική) ρίζα. Το υπόρριζο λοιπόν θα πρέπει να είναι μεγαλύτερο ή ίσο με το 0. Έτσι θα πρέπει να δεχτούμε στο Πεδίο Ορισμού μόνο εκείνες τις τιμές του x για τις οποίες ισχύει:
ανήκει σε αυτή τη κατηγορία αφού στον τύπο της εμφανίζεται μια τουλάχιστον (τετραγωνική) ρίζα. Το υπόρριζο λοιπόν θα πρέπει να είναι μεγαλύτερο ή ίσο με το 0. Έτσι θα πρέπει να δεχτούμε στο Πεδίο Ορισμού μόνο εκείνες τις τιμές του x για τις οποίες ισχύει: ![]() . Συμπεραίνουμε τώρα ότι το Πεδίο Ορισμού της συνάρτησης h είναι:
. Συμπεραίνουμε τώρα ότι το Πεδίο Ορισμού της συνάρτησης h είναι: ![]() .
.
π.χ.2 Στη συνάρτηση ![]() υπάρχουν δύο υπόρριζα (η παράσταση 2x-8 και η παράσταση x-8) και ένας παρονομαστής (η παράσταση
υπάρχουν δύο υπόρριζα (η παράσταση 2x-8 και η παράσταση x-8) και ένας παρονομαστής (η παράσταση ![]() ). Γι’ αυτό το λόγο απαιτούμε τα παρακάτω:
). Γι’ αυτό το λόγο απαιτούμε τα παρακάτω:
![Rendered by QuickLaTeX.com \[\left{\begin{matrix}2x-8\geq 0\Leftrightarrow 2x\geq 8\Leftrightarrow x\geq 4\\ \mathit{\kappa \alpha \iota }\\ x-8\geq 0\Leftrightarrow x\geq 8\\ \mathit{\kappa \alpha \iota }\\ \sqrt{x-8}\neq0\Leftrightarrow x-8\neq0\Leftrightarrow x\neq8\end{matrix}\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-45ac75147f615b071fda201a0c111c99_l3.png)
αλλά όλα αυτά μαζί μας δίνουν x>8 . Επομένως το Πεδίο Ορισμού της συνάρτησης t είναι το ![]() .
.
Καταλήγουμε τελικά στο εξής:
[su_box type=»info» title=»Tip 2″ color=»#0000FF»] όταν θέλουμε να βρούμε το πεδίο ορισμού μιας άρρητης συνάρτησης της μορφής ![]() λύνουμε την ανίσωση
λύνουμε την ανίσωση ![]() και γράφουμε Df={οι λύσεις της ανίσωσης
και γράφουμε Df={οι λύσεις της ανίσωσης ![]() }[/su_box]
}[/su_box]
Στη Β΄ Λυκείου είδαμε για πρώτη φορά τους λογάριθμους και «μελετήσαμε» τη λογαριθμική συνάρτηση ![]() όπου μάθαμε, εκτός των άλλων, ότι το Πεδίο Ορισμού της είναι το
όπου μάθαμε, εκτός των άλλων, ότι το Πεδίο Ορισμού της είναι το ![]() . Γι’ αυτό όταν σε μια συνάρτηση συναντήσουμε λογάριθμο θα πρέπει να αναζητάμε τα x εκείνα για τα οποία το «περιεχόμενο» του λογάριθμου να είναι θετικό. Για παράδειγμα η συνάρτηση
. Γι’ αυτό όταν σε μια συνάρτηση συναντήσουμε λογάριθμο θα πρέπει να αναζητάμε τα x εκείνα για τα οποία το «περιεχόμενο» του λογάριθμου να είναι θετικό. Για παράδειγμα η συνάρτηση ![]() , έχει Πεδίο Ορισμού το σύνολο
, έχει Πεδίο Ορισμού το σύνολο ![]() αφού πρέπει x-6>0 δηλαδή x>6.
αφού πρέπει x-6>0 δηλαδή x>6.
Συμπέρασμα,
[su_box type=»info» title=»Tip 3″ color=»#0000FF»] όταν θέλουμε να βρούμε το πεδίο ορισμού μιας λογαριθμικής συνάρτησης της μορφής ![]() λύνουμε την ανίσωση g(x)>0 και γράφουμε Df={οι λύσεις της ανίσωσης g(x)>0}[/su_box]
λύνουμε την ανίσωση g(x)>0 και γράφουμε Df={οι λύσεις της ανίσωσης g(x)>0}[/su_box]
ΠΑΡΑΤΗΡΗΣΕΙΣ – ΣΧΟΛΙΑ:
- Αν η συνάρτηση της οποίας ζητάμε το Πεδίο Ορισμού δεν έχει ούτε παρονομαστές, ούτε ρίζες, ούτε λογάριθμους που να περιέχουν μεταβλητή, τότε δεν υπάρχουν περιορισμοί κι επομένως το Πεδίο Ορισμού αυτής της συνάρτησης θα είναι όλοι οι πραγματικοί αριθμοί (
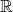 ).
).
π.χ. η ![]() έχει
έχει ![]() αφού δεν υπάρχει x σε παρονομαστή, ρίζα ή λογάριθμο.
αφού δεν υπάρχει x σε παρονομαστή, ρίζα ή λογάριθμο.
- Απ’ την άλλη μεριά όμως αν από τον τύπο μιας συνάρτησης f(x) προκύπτουν περισσότεροι του ενός περιορισμοί, είμαστε υποχρεωμένοι να τους χρησιμοποιήσουμε όλους για να βρούμε ποια είναι τελικά αυτά τα x που πληρούν τις προϋποθέσεις που θέλουμε. Ένα τέτοιο παράδειγμα είδαμε παραπάνω με την συνάρτηση
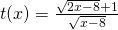 η οποία είχε x και σε παρονομαστή αλλά και σε ρίζες. Στο παράδειγμα αυτό πήραμε τους απαραίτητους περιορισμούς και για τις ρίζες αλλά και για τον παρονομαστή κι αφού λύσαμε τον καθένα ξεχωριστά βρήκαμε την κοινή τους λύση (στην πραγματικότητα λύσαμε ένα σύστημα).
η οποία είχε x και σε παρονομαστή αλλά και σε ρίζες. Στο παράδειγμα αυτό πήραμε τους απαραίτητους περιορισμούς και για τις ρίζες αλλά και για τον παρονομαστή κι αφού λύσαμε τον καθένα ξεχωριστά βρήκαμε την κοινή τους λύση (στην πραγματικότητα λύσαμε ένα σύστημα). - Επειδή στη Γ΄ Λυκείου θα συναντήσουμε πολλές φορές τριγωνομετρικές συναρτήσεις καλό είναι να επισημάνουμε ότι η εφαπτομένη αλλά και η συνεφαπτομένη έχουν παρονομαστές παρότι δεν φαίνονται (αρκεί να θυμηθούμε ότι
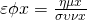 και
και 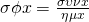 ). Έτσι θα χρειαστεί να πάρουμε τους παρακάτω περιορισμούς:
). Έτσι θα χρειαστεί να πάρουμε τους παρακάτω περιορισμούς:
για την ![]() ,
, ![]() με
με ![]()
για την ![]() ,
, ![]() με
με ![]()
-
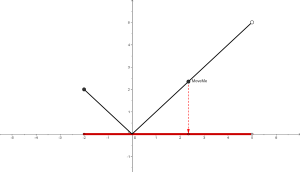
Το Πεδίο Ορισμού της συνάρτησης είναι το κόκκινο διάστημα πάνω στον οριζόντιο άξονα Το Πεδίο Ορισμού μιας συνάρτησης θα μπορούσε να βρεθεί και από τη γραφική παράσταση της συνάρτησης ( στη περίπτωση που δίνεται αυτή ). Για να δείτε πως κάντε κλικ στην εικόνα.
- Για τους μαθητές που παρακολουθούν τα μαθήματα της θετικής ή τεχνολογικής κατεύθυνσης θα πρέπει να αναφέρουμε και δύο ακόμη περιπτώσεις που θα συναντήσουν:
- Συναρτήσεις της μορφής
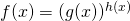 : Πρέπει η βάση g(x) να είναι θετική και διάφορη του 1 (στη περίπτωση που το g(x)=1 ορίζεται η f αλλά είναι σταθερή αφού f(x)=1h(x)=1 για κάθε x)
: Πρέπει η βάση g(x) να είναι θετική και διάφορη του 1 (στη περίπτωση που το g(x)=1 ορίζεται η f αλλά είναι σταθερή αφού f(x)=1h(x)=1 για κάθε x) - Συναρτήσεις οι οποίες έχουν προκύψει από την «σύνθεση» δύο άλλων συναρτήσεων: Για την περίπτωση της «σύνθεσης συναρτήσεων» όμως θα αναφερθούμε αναλυτικά σε άλλο άρθρο.
- Συναρτήσεις της μορφής
Αν θέλετε να κάνετε εξάσκηση στα παραπάνω μπορείτε να κατεβάσετε ένα αρχείο με ασκήσεις κάνοντας κλικ στον παρακάτω σύνδεσμο. Μη διστάσετε να στείλετε τις λύσεις ή να ρωτήσετε τυχόν απορίες , στέλνοντας ένα e-mail ή αφήνοντας ένα σχόλιο στο τέλος του άρθρου.

Θέλω να μάθω…πως δείχνουμε ότι τρία σημεία είναι συνευθειακά
Η βασική μεθοδολογία με την οποία αποδεικνύουμε ότι τρία σημεία με γνωστές συντεταγμένες είναι συνευθειακά (βρίσκονται και τα τρία στην ίδια ευθεία). Στο άρθρο θα βρείτε τρεις διαφορετικούς τρόπους επίλυσης τέτοιων προβλημάτων.
 Συνευθειακά Σημεία
Συνευθειακά Σημεία
(Μαθηματικά Κατεύθυνσης Β΄ Λυκείου)
Μπορούμε να αποδείξουμε ότι τρία σημεία είναι συνευθειακά με τρεις διαφορετικούς τρόπους ανάλογα με το σημείο στο οποίο έχουμε φτάσει στην ύλη μας στο σχολείο (Μαθηματικά Κατεύθυνσης Β΄ Λυκείου).
Έστω λοιπόν ότι έχουμε τα σημεία Α(1,3), Β(2,5) και Γ(4,9)
- 1ος τρόπος, με διανύσματα
Κατ’ αρχάς φτιάχνουμε δύο διανύσματα με άκρα αυτά τα σημεία έστω τα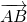 και
και 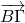 (Υπενθύμιση 1η),
(Υπενθύμιση 1η),
![Rendered by QuickLaTeX.com \[\overrightarrow{AB}=(2-1,5-3)=(1,2)\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-b6b0e60b4cd01bc4a278e3331e7574cf_l3.png)
και
![Rendered by QuickLaTeX.com \[\overrightarrow{B\Gamma}=(4-2,9-5)=(2,4)\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-7acac74d9a68a60475a3f4c3a3e65b3e_l3.png)
στη συνέχεια αποδεικνύουμε ότι αυτά τα διανύσματα είναι παράλληλα είτε με τους συντελεστές διεύθυνσης (Υπενθύμιση 2η)
![Rendered by QuickLaTeX.com \[\lambda_{\overrightarrow{AB}}=2/1=\lambda_{\overrightarrow{A\Gamma}}=4/2=2\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-52c2565b00f9d08a8a0369920c2fb182_l3.png)
είτε με την ορίζουσα (Υπενθύμιση 3η)
![Rendered by QuickLaTeX.com \[\det(\overrightarrow{AB},\overrightarrow{B\Gamma})=\begin{vmatrix}1 \:2 \\ 2\: 4\end{vmatrix}=1\cdot 4-2\cdot2=0\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-417ab8963772b356fca256c0175165be_l3.png)
Αυτό όμως ταυτόχρονα μας δείχνει ότι τα σημεία Α,Β και Γ είναι συνευθειακά γιατί για να είναι παράλληλα τα δύο διανύσματα θα πρέπει είτε να βρίσκονται σε παράλληλους φορείς πράγμα αδύνατο αφού έχουν ένα κοινό σημείο, το Β είτε να βρίσκονται στον ίδιο φορέα στην ίδια ευθεία δηλαδή.
[box type=»info»] Υπενθύμιση 1η:
αν ![]() και
και ![]() δύο σημεία τότε το διάνυσμα
δύο σημεία τότε το διάνυσμα
![]()
[/box]
[box type=»info»] Υπενθύμιση 2η:
Ένα διάνυσμα ![]() έχει συντελεστή διεύθυνσης
έχει συντελεστή διεύθυνσης ![]() εννοείται
εννοείται ![]() [/box]
[/box]
[box type=»info»] Υπενθύμιση 3η:
![]() [/box]
[/box]
- 2ος τρόπος, με ευθείες
Με το ίδιο σκεπτικό μπορούμε να δείξουμε ότι τα τρία σημεία βρίσκονται στην ίδια ευθεία αποδεικνύοντας ότι δύο ευθείες από αυτές που διέρχονται από τα Α,Β, και Γ είναι παράλληλες (δηλαδή έχουν τον ίδιο συντελεστή διεύθυνσης).Έτσι λοιπόν βρίσκουμε το συντελεστή διεύθυνσης της ΑΒ και ΒΓ(Υπενθύμιση 4η) κι έχουμε![Rendered by QuickLaTeX.com \[\lambda_{AB}=\frac{5-3}{2-1}=\lambda_{B\Gamma}=\frac{9-5}{4-2}=2\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-66bd8a4631a1140e2eef8b1b5ea3a3c6_l3.png)
Δύο ευθείες όμως με ένα κοινό σημείο (το Β) δεν γίνεται να είναι παράλληλες. Τι συμβαίνει τότε; Οι δύο ευθείες ταυτίζονται δηλαδή δεν είναι δύο αλλά μόνο μία ευθεία.
[box type=»info»] Υπενθύμιση 4η:
αν μια ευθεία (ε) διέρχεται από τα σημεία ![]() και
και ![]() τότε ο συντελεστής διεύθυνσής της είναι:
τότε ο συντελεστής διεύθυνσής της είναι:
![]()
[/box]
- 3ος τρόπος, με τρίγωνα

Κάντε κλικ στην εικόνα για να «παίξετε» Αρκεί να δείξουμε ότι το τρίγωνο ΑΒΓ έχει εμβαδό ίσο με 0, γιατί αυτό απλά σημαίνει ότι δεν υπάρχει τρίγωνο ΑΒΓ δηλαδή τα σημεία Α,Β και Γ δεν σχηματίζουν τρίγωνο γιατί βρίσκονται πάνω στην ίδια ευθεία (συνευθειακά). Έτσι λοιπόν στο παράδειγμά μας έχουμε
![Rendered by QuickLaTeX.com \[(AB\Gamma)=\frac{1}{2}\left|\det(\overrightarrow{AB},\overrightarrow{B\Gamma})\right|=0\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-9bcb76200d26817a62346b00263f3315_l3.png)
![Rendered by QuickLaTeX.com \[\Leftrightarrow \det(\overrightarrow{AB},\overrightarrow{B\Gamma})=0\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-d0b84dafc997672944c958c06eeb95ae_l3.png)
που ισχύει (τις πράξεις τις κάναμε προηγούμενα στον 1ο τρόπο).
Θέλω να μάθω … να λύνω κλασματικές εξισώσεις
Ας δούμε ποια εξίσωση λέγεται κλασματική, πως βρίσκουμε τις λύσεις της και πως τους περιορισμούς. Δείτε πόσο σημαντικό είναι να μην ξεχνάμε να παίρνουμε περιορισμούς κάθε φορά που μια μεταβλητή εμφανίζεται σε παρονομαστή.
Κατ’ αρχάς ας δούμε τι εννοούμε όταν λέμε «κλασματικές εξισώσεις». Πολλοί μπορεί να θεωρούν ότι μια εξίσωση που έχει κλάσματα είναι μια κλασματική εξίσωση. Αυτό όμως δεν είναι σωστό γιατί μια εξίσωση τη λέμε κλασματική μόνο στη περίπτωση που υπάρχει άγνωστος σε ένα τουλάχιστον παρονομαστή της. Έτσι λοιπόν η εξίσωση ![]() ναι μεν έχει κλάσματα αλλά δεν είναι κλασματική αφού δεν υπάρχει άγνωστος σε κανένα παρονομαστή, ενώ η εξίσωση
ναι μεν έχει κλάσματα αλλά δεν είναι κλασματική αφού δεν υπάρχει άγνωστος σε κανένα παρονομαστή, ενώ η εξίσωση ![]() σύμφωνα με αυτά που προαναφέραμε είναι μια κλασματική εξίσωση αφού ο άγνωστος x «κυκλοφορεί» σε παρονομαστές. Δηλαδή ο x «δουλεύει υπογείως (ύπουλα)» πράγμα επικίνδυνο όπως θα δούμε παρακάτω.
σύμφωνα με αυτά που προαναφέραμε είναι μια κλασματική εξίσωση αφού ο άγνωστος x «κυκλοφορεί» σε παρονομαστές. Δηλαδή ο x «δουλεύει υπογείως (ύπουλα)» πράγμα επικίνδυνο όπως θα δούμε παρακάτω.
Στη συνέχεια θα επιλύσουμε μια κλασματική εξίσωση για να δούμε ποια μέθοδο ακολουθούμε και τι πρέπει να προσέξουμε.
Να βρείτε τις λύσεις της παρακάτω εξίσωσης ![]()
[wptabs mode=»horizontal»] [wptabtitle] Επίλυση[/wptabtitle] [wptabcontent]
|
Όπως σε όλες τις κατηγορίες εξισώσεων το πρώτο πράγμα που πρέπει να κάνουμε είναι να απαλλαγούμε από τους παρονομαστές (αν υπάρχουν) |
|
|
Για να το πετύχουμε αυτό πρέπει να παραγοντοποιήσουμε όσους από τους παρονομαστές παραγοντοποιούνται. Στην άσκησή μας ο μόνος που μπορεί να παραγοντοποιηθεί είναι ο |
|
|
Τώρα είμαστε σε θέση να βρούμε το Ε.Κ.Π., που είναι το γινόμενο όλων των παρονομαστών με την προϋπόθεση όμως κάθε παράγοντας να εμφανίζεται μία μόνο φορά και μάλιστα στη μεγαλύτερη δύναμη. Στο παράδειγμά μας το Ε.Κ.Π.=χ(χ+3). Πολλαπλασιάζουμε τώρα όλους τους όρους της εξίσωσης με το Ε.Κ.Π. |
|
|
Μετά από τις απλοποιήσεις έχουμε μια εξίσωση χωρίς παρονομαστές, όπως φαίνεται δίπλα. Σειρά τώρα για «αποχώρηση» έχουν οι παρενθέσεις ώστε να απελευθερώσουμε το x. Αυτό γίνεται με τη βοήθεια της επιμεριστικής ιδιότητας |
|
|
Συμμαζεύοντας λίγο (κάνουμε αναγωγή όμοιων όρων) θα προκύψει μια εξίσωση 1ου (οπότε χωρίζουμε γνωστούς – άγνωστους κτλ) ή 2ου βαθμού (τα μεταφέρουμε όλα στο ένα μέλος, υπολογίζουμε τη διακρίνουσα κτλ). Στην άσκηση που προσπαθούμε να λύσουμε τώρα παρότι δείχνει δεύτερου βαθμού (αφού έχει x2) αν τη δουλέψουμε λίγο θα δούμε ότι μετά την αναγωγή των όμοιων όρων θα προκύψει μια εξίσωση πρώτου βαθμού οπότε |
|
|
βρίσκουμε τελικά πως η εξίσωση που μας δόθηκε έχει λύση τον αριθμό -3. |
Μετά από αρκετό κόπο θα έλεγα φτάσαμε στο να βρούμε ότι η εξίσωση ![]() έχει λύση το x=-3.
έχει λύση το x=-3.

Κι όμως έχουμε κάνει ΜΕΓΑΛΟ ΛΑΘΟΣ κι αν έχεις κάνει το κόπο να φτάσεις μέχρι εδώ καλό θα ήταν να κάνεις κλικ στην καρτέλα «Περιορισμοί» για να δεις ποιο είναι το λάθος που κάναμε και πόσο σοβαρό είναι.
Επιστροφή^^^
[/wptabcontent]
[wptabtitle]Περιορισμοί[/wptabtitle] [wptabcontent]Όταν έχουμε να λύσουμε μια εξίσωση αναζητούμε ποια τιμή (ή ποιες τιμές) μπορεί να πάρει η άγνωστη μεταβλητή έτσι ώστε αν την αντικαταστήσουμε στην εξίσωση να προκύψει μια αληθής ισότητα (για παράδειγμα η λύση της εξίσωσης 2χ-8=0 είναι ο αριθμός 4 γιατί αν αντικαταστήσουμε το χ με τον αριθμό 4 θα προκύψει 2.4-8=0 που είναι μια σωστή πρόταση.
Στο προηγούμενο όμως άρθρο είχαμε αναφερθεί στους περιορισμούς (κάντε κλικ εδώ για να το δείτε). Εκεί λοιπόν είπαμε ότι δεν έχει νόημα στα μαθηματικά κλάσμα με παρονομαστή το 0. Γιαυτό όταν λύνουμε κλασματικές εξισώσεις θα πρέπει εκ των προτέρων να θέτουμε περιορισμούς για τον άγνωστο. Δηλαδή από την αρχή να δηλώνουμε ότι για τον άγνωστο, έστω χ, δεν μπορούμε να δεχτούμε κάποιες τιμές γιατί μηδενίζουν κάποιον από τους παρονομαστές της εξίσωσης.
Κατά την επίλυση μιας εξίσωσης σε όποια κατηγορία κι αν ανήκει αυτή (1ου ή 2ου βαθμού ή και κλασματική) σε κάθε μας βήμα (όταν διώχνουμε παρονομαστές, παρενθέσεις κτλ) δημιουργούμε μια άλλη εξίσωση πιο απλή από την αρχική που έχει ως λύσεις της τις λύσεις της προηγούμενης αλλά πιθανόν να έχει κι άλλες (περισσότερες). Στο τέλος τις επιπλέον λύσεις θα πρέπει να τις απορρίψουμε, να μην τις δεχτούμε δηλαδή ως λύσεις της αρχικής εξίσωσης. Αυτό ακριβώς έχει συμβεί και με την εξίσωση ![]() γιατί στην πορεία πήρε διάφορες μορφές μέχρι που κατέληξε να γίνει 4χ=-12. Εμείς βρήκαμε ότι χ=-3 αυτή όμως η λύση είναι η λύση της 4χ=-12 (γιατί αν βάλουμε όπου χ το -3 προκύπτει μια αληθής πρόταση η 4.(-3)=-12 και όχι της
γιατί στην πορεία πήρε διάφορες μορφές μέχρι που κατέληξε να γίνει 4χ=-12. Εμείς βρήκαμε ότι χ=-3 αυτή όμως η λύση είναι η λύση της 4χ=-12 (γιατί αν βάλουμε όπου χ το -3 προκύπτει μια αληθής πρόταση η 4.(-3)=-12 και όχι της ![]() γιατί εδώ δεν μπορούμε καν να βάλουμε όπου χ το -3 αφού θα μας μηδενίσει κάποιους παρονομαστές (τον χ2+3χ και τον χ+3).
γιατί εδώ δεν μπορούμε καν να βάλουμε όπου χ το -3 αφού θα μας μηδενίσει κάποιους παρονομαστές (τον χ2+3χ και τον χ+3).
Τι πρέπει να κάνουμε λοιπόν σε τέτοιες περιπτώσεις;
Πρέπει να παίρνουμε τα μέτρα μας, δηλαδή να παίρνουμε περιορισμούς.
ΚΑΘΕ ΠΑΡΟΝΟΜΑΣΤΗΣ ΠΡΕΠΕΙ ΝΑ ΜΗΝ ΓΙΝΕΤΑΙ ΙΣΟΣ ΜΕ 0
κι επειδή μέσα στο Ε.Κ.Π. είναι «κρυμμένοι» όλοι οι παρονομαστές της εξίσωσης είναι αρκετό να απαιτούμε
ΤΟ Ε.Κ.Π. ΝΑ ΜΗΝ ΓΙΝΕΤΑΙ ΠΟΤΕ ΙΣΟ ΜΕ 0 (![]() ).
).
Στη συγκεκριμένη επομένως άσκηση θα έπρεπε την ώρα που βρήκαμε το Ε.Κ.Π. να γράφαμε: ![]() πράγμα που σημαίνει ότι και το x αλλά και το x+3 πρέπει να είναι διάφορα του 0 δηλαδή με άλλα λόγια δεν μπορούμε να δεχτούμε σαν λύσεις ούτε το 0 αλλά ούτε και το -3. Πιο σύντομα και πιο «μαθηματικά» όλα τα παραπάνω θα μπορούσαν να γραφούν ως εξής:
πράγμα που σημαίνει ότι και το x αλλά και το x+3 πρέπει να είναι διάφορα του 0 δηλαδή με άλλα λόγια δεν μπορούμε να δεχτούμε σαν λύσεις ούτε το 0 αλλά ούτε και το -3. Πιο σύντομα και πιο «μαθηματικά» όλα τα παραπάνω θα μπορούσαν να γραφούν ως εξής:
![]()
![]()
![]()
Βλέπουμε λοιπόν ότι η εξίσωση που λύναμε τελικά δεν έχει λύση το -3 , άρα δεν έχει καμία λύση ήταν δηλαδή αδύνατη. Ξεχνώντας όμως τους περιορισμούς «την πατήσαμε». Επιστροφή^^^
[/wptabcontent]
[wptabtitle]Σε Έκτακτη Περίπτωση[/wptabtitle] [wptabcontent]Αν σε κάποια περίπτωση αδυνατούμε να βρούμε τους περιορισμούς είτε γιατί κάποιος δυσκολεύεται είτε γιατί δεν προλαβαίνει (π.χ. σε διαγώνισμα) τότε μπορεί να αποφύγει τα παραπάνω και απλώς να ελέγξει αν οι λύσεις που βρήκε μηδενίζουν το Ε.Κ.Π. και
αν το Ε.Κ.Π. μηδενίζεται, τότε η λύση απορρίπτεται αν όχι γίνεται δεκτή.
Στην άσκησή μας το Ε.Κ.Π. =![]() για x=-3 γίνεται Ε.Κ.Π.=-3.(-3+3)=-3.0=0 κι επομένως η λύση x=-3 απορρίπτεται.
για x=-3 γίνεται Ε.Κ.Π.=-3.(-3+3)=-3.0=0 κι επομένως η λύση x=-3 απορρίπτεται.
Μπορεί να σας κούρασα με την μεγάλη έκταση που είχε το άρθρο αλλά θεωρώ τις κλασματικές εξισώσεις λιγάκι δύσκολες για μαθητές Γ΄ Γυμνασίου αλλά και πολύ σημαντικές για τη συνέχεια. Αυτό που πρέπει να θυμόμαστε τελικά είναι πως οι κλασματικές εξισώσεις λύνονται όπως και όλες οι υπόλοιπες δηλαδή:
- διώχνουμε παρονομαστές (πολλαπλασιάζοντας με το Ε.Κ.Π.)
- διώχνουμε παρενθέσεις (με επιμεριστική)
- συμμαζεύουμε λίγο (αναγωγή όμοιων όρων)
έτσι προκύπτει μια εξίσωση 1ου ή 2ου βαθμού που λύνουμε ανάλογα και
τέλος
ΔΕΝ ΞΕΧΝΑΜΕ ΝΑ ΕΛΕΓΞΟΥΜΕ ΑΝ ΟΙ ΛΥΣΕΙΣ ΠΟΥ ΒΡΗΚΑΜΕ ΠΕΡΝΟΥΝ ΤΟ (CRASH) TEST ΤΩΝ ΠΕΡΙΟΡΙΣΜΩΝ (δηλαδή να μην μηδενίζουν το Ε.Κ.Π.).
[/wptabcontent][/wptabs]
Θέλω να μάθω να λύνω … τριγωνομετρικές εξισώσεις
 Τριγωνομετρική εξίσωση λέγεται η εξίσωση στην οποία ο άγνωστος είναι «φυλακισμένος» μέσα σε κάποιο τριγωνομετρικό αριθμό. Οι τριγωνομετρικές εξισώσεις (λόγω της περιοδικότητας που παρουσιάζουν οι τριγωνομετρικές συναρτήσεις) έχουν άπειρες λύσεις που χωρίζονται σε δύο ομάδες. Για να μπορέσουμε να λύσουμε τριγωνομετρικές εξισώσεις θα πρέπει να ελευθερώσουμε τον άγνωστο μέσα από τον τριγωνομετρικό αριθμό, για να το πετύχουμε αυτό ακολουθούμε τα παρακάτω βήματα:
Τριγωνομετρική εξίσωση λέγεται η εξίσωση στην οποία ο άγνωστος είναι «φυλακισμένος» μέσα σε κάποιο τριγωνομετρικό αριθμό. Οι τριγωνομετρικές εξισώσεις (λόγω της περιοδικότητας που παρουσιάζουν οι τριγωνομετρικές συναρτήσεις) έχουν άπειρες λύσεις που χωρίζονται σε δύο ομάδες. Για να μπορέσουμε να λύσουμε τριγωνομετρικές εξισώσεις θα πρέπει να ελευθερώσουμε τον άγνωστο μέσα από τον τριγωνομετρικό αριθμό, για να το πετύχουμε αυτό ακολουθούμε τα παρακάτω βήματα:
Βήμα 10
Απομονώνουμε τον τριγωνομετρικό αριθμό που περιέχει τον άγνωστο στο ένα μέλος.
Βήμα 20
Βρίσκουμε μια «αρχική λύση» για την εξίσωσή μας, δηλαδή μια γωνία από 0ο εως 360ο που να ικανοποιεί την εξίσωση.
Βήμα 30
Χρησιμοποιούμε τους παρακάτω τύπους λύσεων, ανάλογα με την περίπτωση:
Τύποι λύσεων για τριγωνομετρικές εξισώσεις
| Εξίσωση | Λύσεις ( |
|---|---|
Ας δούμε κι ένα παράδειγμα για να καταλάβουμε καλύτερα τη διαδικασία επίλυσης μιας τριγωνομετρικής εξίσωσης:
Άσκηση: Να λυθεί η εξίσωση ![]()
Λύση:
Βήμα 10: απομονώνουμε το συνημίτονο (το θεωρούμε ως άγνωστο, χωρίζουμε γνωστούς από άγνωστους και διαιρούμε με το συντελεστή του άγνωστου)
![]()
![]()
![]()
Βήμα 20: Βρίσκουμε μια γωνία στο διάστημα [0 – 2π] που να ικανοποιεί την εξίσωση αυτή.
Η γωνία π/3 έχει συνημίτονο ίσο με 1/2, δηλαδή
![]() και
και ![]()

άρα ισχύει
![]()
Βήμα 3ο: Από τους τύπους των λύσεων παίρνω,
![]() ή
ή ![]() με
με ![]()
Περισσότερες λυμένες ασκήσεις μπορείτε να βρείτε εδώ.
Θέλω να μάθω τι είναι η αλγεβρική παράσταση
Πριν ξεκινήσουμε να πούμε τι είναι η αλγεβρική παράσταση καλό θα ήταν να δούμε πρώτα τι είναι η αριθμητική παράσταση.
Αριθμητική παράσταση

Μία παράσταση που αποτελείται από αριθμούς οι οποίοι συνδέονται μεταξύ τους με τα σύμβολα των πράξεων (πρόσθεση, αφαίρεση, πολλαπλασιασμό, δύναμη και πιθανόν παρένθεση), ονομάζεται αριθμητική παράσταση.
Έτσι αριθμητικές παραστάσεις είναι και οι: ![]() ,
, ![]()
Όταν σε μια αριθμητική παράσταση εκτελέσουμε τις πράξεις προκύπτει ένας και μοναδικός αριθμός που λέγεται τιμή της αριθμητικής παράστασης. Στα δύο προηγούμενα παραδείγματα έχουμε:
![]() και
και ![]() (Σχόλιο)
(Σχόλιο)
Αλγεβρική παράσταση
Όταν όμως σε μια παράσταση εκτός από αριθμούς υπάρχουν και μεταβλητές (γράμματα δηλαδή που παριστάνουν αριθμούς) που συνδέονται μεταξύ τους με τα σύμβολα των πράξεων, τότε λέμε ότι έχουμε μια αλγεβρική παράσταση. Για παράδειγμα, αλγεβρικές παραστάσεις είναι οι
![]() ,
, ![]() ,
, ![]()

Στις αλγεβρικές παραστάσεις μπορούμε να αντικαταστήσουμε τα γράμματα με διάφορους αριθμούς (γι’ αυτό το λόγο λέγονται και μεταβλητές). Όταν σε μια αλγεβρική παράσταση αντικαταστήσουμε τα γράμματα που περιέχει με κάποιους αριθμούς αυτό που θα προκύψει θα είναι μια αριθμητική παράσταση, κι αν στη συνέχεια εκτελέσουμε και τις πράξεις θα καταλήξουμε να έχουμε έναν αριθμό.
Έτσι αν στην αλγεβρική παράσταση ![]() αντικαταστήσουμε το x με τον αριθμό 3, θα έχουμε
αντικαταστήσουμε το x με τον αριθμό 3, θα έχουμε ![]() . Ο αριθμός 7 λέγεται τιμή της παράστασης για x=3. Πιο καλά διαβάζουμε ως εξής: Η τιμή της παράστασης
. Ο αριθμός 7 λέγεται τιμή της παράστασης για x=3. Πιο καλά διαβάζουμε ως εξής: Η τιμή της παράστασης ![]() για x=3 είναι 7.
για x=3 είναι 7.
Με παρόμοιο τρόπο βρίσκουμε ότι η τιμή της παράστασης
![]()
για x=1 και y=2 είναι
![]()
ενώ η τιμή της
![]()
για χ=-4 είναι
![]()
Δείτε εδώ βίντεο με θέμα τις αλγεβρικές παραστάσεις
_________________________________
Σχόλιο: Θυμηθείτε τη σειρά με την οποία πρέπει να κάνουμε τις πράξεις
- Δυνάμεις
- Πολλαπλασιασμοί – Διαιρέσεις
- Προσθέσεις – αφαιρέσεις
Στην περίπτωση που υπάρχουν παρενθέσεις ξεκινάμε τις πράξεις μέσα από τις παρενθέσεις αλλά και πάλι με την προηγούμενη σειρά.
__________________________________Επιστροφή
Επίλυση δευτεροβάθμιας εξίσωσης
Αφού είδαμε θεωρητικά το πως μπορούμε να βρούμε τις λύσεις μιας δευτεροβάθμιας εξίσωσης, καλό θα ήταν να το εφαρμόσουμε και στην πράξη
Θέλω να μάθω … πως να βρίσκω τις λύσεις σε μια εξίσωση 2ου βαθμού
Εξίσωση 2ου βαθμού (ή δευτεροβάθμια εξίσωση) είναι η εξίσωση που περιέχει έναν άγνωστο (π.χ. τον x) και έχει ή μπορεί να πάρει τη μορφή ![]() με
με ![]() .
.
Όταν μας δώσουν μια εξίσωση για να βρούμε τις λύσεις της και δεν είναι στη παραπάνω μορφή δεν γνωρίζουμε αν πράγματι είναι δευτεροβάθμια εξίσωση ή όχι. Γι’ αυτό είμαστε υποχρεωμένοι να κάνουμε κάποια «προεργασία» ώστε να είμαστε σε θέση να αντιληφθούμε το βαθμό της εξίσωσης και κατόπιν να ψάξουμε να βρούμε τις λύσεις. Γιατί με άλλο τρόπο δουλεύουμε στις εξισώσεις πρώτου βαθμού, με άλλο σε αυτές που είναι δεύτερου βαθμού, διαφορετικά στις τριτοβάθμιες κ.ο.κ. Όσον αφορά στις πρωτοβάθμιες εξισώσεις έχουμε δώσει τη μεθοδολογία εδώ.
Η «προεργασία» λοιπόν που πρέπει να γίνει είναι ήδη γνωστή, θα πρέπει:
- να απαλλάξουμε την εξίσωση από τους παρονομαστές που τυχόν έχει
(πολλαπλασιάζοντας όλους τους όρους με το ΕΚΠ των παρονομαστών)
- να διώξουμε τις παρενθέσεις
(με χρήση της επιμεριστικής ιδιότητας) και τέλος - να κάνουμε αναγωγή όμοιων όρων
(να «συμμαζέψουμε» την εξίσωση προσθέτοντας μεταξύ τους τους όμοιους όρους)
Σε αυτό το σημείο είμαστε σε θέση να δούμε το βαθμό της εξίσωσης και αν
- ο άγνωστος δεν είναι υψωμένος σε καμία δύναμη, τότε έχουμε να λύσουμε μια πρωτοβάθμια εξίσωση κατά τα γνωστά (χωρίζουμε γνωστούς – άγνωστους κ.τ.λ.)
- η μεγαλύτερη δύναμη στην οποία εμφανίζεται ο άγνωστος είναι το τετράγωνο, τότε είμαστε στη περίπτωση της δευτεροβάθμιας εξίσωσης και η διαδικασία που ακολουθούμε για να βρούμε τις λύσεις είναι η παρακάτω:
- Μεταφέρουμε όλους τους όρους στο ένα μέλος ώστε η εξίσωση να πάρει τη μορφή
![Rendered by QuickLaTeX.com \[\alpha\chi^2+\beta\chi+\gamma=0\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-81ace40d7c80db6a6ba0536fc9fb3af2_l3.png)
- Ξεκαθαρίζουμε ποιοι αριθμοί παίζουν το ρόλο των α, β και γ (α: ο συντελεστής του χ2, β: ο συντελεστής του χ και γ ο σταθερός όρος).
- Με τη βοήθεια των α, β, γ και του τύπου
![Rendered by QuickLaTeX.com \[\Delta=\beta^2-4\alpha\gamma\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-5d415ece8e5ba7b1aecd03b1a3fc7504_l3.png)
υπολογίζουμε ένα νέο αριθμό τον Δ που λέγεται «Διακρίνουσα» (διάβασε το Σχόλιο1 παρακάτω)
- Από το «είδος» αυτού του αριθμού, του Δ, εξαρτάται κα το πως θα προχωρήσουμε παρακάτω. Και πιο συγκεκριμένα:
- αν η Διακρίνουσα (Δ) είναι αρνητικός αριθμός, τότε η εξίσωση μας δεν έχει λύσεις, είναι όπως λέμε σε τέτοιες περιπτώσεις αδύνατη
- αν η Διακρίνουσα (Δ) είναι θετικός αριθμός, τότε η εξίσωση έχει 2 λύσεις διαφορετικές μεταξύ τους και που τις υπολογίζουμε από τους τύπους
![Rendered by QuickLaTeX.com \[\chi_1=\frac{-\beta-\sqrt{\Delta}}{2\alpha}\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-69010efac1192b69e8f519e706b5b494_l3.png)
και
![Rendered by QuickLaTeX.com \[\chi_2=\frac{-\beta+\sqrt{\Delta}}{2\alpha}\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-d821ee0f34f5ff8251b1eb2d5d5dca16_l3.png)
(διάβασε το Σχόλιο2)
- αν η Διακρίνουσα (Δ) είναι ίση με 0, τότε η εξίσωση έχει δύο ίσες λύσεις (ή όπως συνήθως λέμε μια διπλή λύση) που μπορούμε να υπολογίσουμε από τον τύπο
![Rendered by QuickLaTeX.com \[\chi_1=\chi_2=\frac{-\beta}{2\alpha}\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-d0834493947d83842b3e5b8053d83815_l3.png)
(Σχόλιο3)
Συνοπτικά η διαδικασία που ακολουθούμε ώστε να βρούμε τις λύσεις σε μια εξίσωση της μορφής
![]()
καθώς και οι περιπτώσεις που μπορούν να προκύψουν φαίνονται στο σχήμα που ακολουθεί:
Λυμένα παραδείγματα για να κατανοήσουμε καλύτερα αυτά που αναφέραμε θα δείτε στο επόμενο άρθρο.
Η παράσταση ![]() συμβολίζεται με Δ και λέγεται «Διακρίνουσα». Η ονομασία δεν είναι τυχαία γιατί η διακρίνουσα μας βοηθάει να διακρίνουμε το πλήθος των ριζών (λύσεων) της εξίσωσης. Πράγματι,
συμβολίζεται με Δ και λέγεται «Διακρίνουσα». Η ονομασία δεν είναι τυχαία γιατί η διακρίνουσα μας βοηθάει να διακρίνουμε το πλήθος των ριζών (λύσεων) της εξίσωσης. Πράγματι,
- Δ<0
 0 λύσεις
0 λύσεις - Δ=0
 1 λύση διπλή
1 λύση διπλή - Δ>0
 2 λύσεις διαφορετικές
2 λύσεις διαφορετικές
Οι δύο αυτοί τύποι μπορούν να γραφούν σε έναν πιο συμμαζεμένο:
![]()
Στην πραγματικότητα ο τύπος αυτός δεν είναι κάποιος νέος τύπος που πρέπει να απομνημονεύσουμε αρκεί να ξέρουμε απ’ έξω τον προηγούμενο τύπο αφού από εκεί προκύπτει και αυτός μόνο που τώρα το Δ είναι 0. Πράγματι,
![]()