πως μας βοηθά η παραγοντοποίηση στην επίλυση εξισώσεων δεύτερου βαθμού ή μεγαλύτερου.
Πριν όμως από αυτό θα πρέπει να δούμε μια σημαντική ιδιότητα:
![Rendered by QuickLaTeX.com \[A \cdot\ B=0\Leftrightarrow \left \{ \begin{matrix} A=0\\ \eta\\ B=0 \end{matrix} \right.\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-94a3e97ff683988e71bf7dccfb4717e3_l3.png)
Η οποία μας λέει ότι ένα γινόμενο είναι ίσο με μηδέν τότε και μόνο τότε αν τουλάχιστον ένας από τους παράγοντες του γινομένου είναι ίσος με μηδέν.
Να δούμε τώρα λύνοντας ένα παράδειγμα πως μπορούμε να εκμεταλλευτούμε τα παραπάνω για να βρούμε τις λύσεις σε μια εξίσωση 2ου βαθμού. Έστω λοιπόν ότι ψάχνουμε να βρούμε εκείνους τους αριθμούς που ικανοποιούν τη σχέση ![]() . Αυτή είναι μια δευτεροβάθμια εξίσωση την οποία και θα μετατρέψω σε γινόμενο (με κάποια από τις μεθόδους παραγοντοποίησης που μάθαμε) με σκοπό να χρησιμοποιήσω την ιδιότητα που προαναφέραμε. Έτσι έχουμε
. Αυτή είναι μια δευτεροβάθμια εξίσωση την οποία και θα μετατρέψω σε γινόμενο (με κάποια από τις μεθόδους παραγοντοποίησης που μάθαμε) με σκοπό να χρησιμοποιήσω την ιδιότητα που προαναφέραμε. Έτσι έχουμε
![]()
(βγάζουμε κοινό παράγοντα το x)
![]()
φτάσαμε λοιπόν στο σημείο να έχουμε ένα γινόμενο που είναι ίσο με το μηδέν. Το γινόμενο αυτό αποτελείται από δύο (πρωτοβάθμιους) παράγοντες τον x και τον x-1. Σύμφωνα με την ιδιότητα που αναφέραμε παραπάνω συμπεραίνουμε ότι τουλάχιστον ένας από αυτούς τους παράγοντες θα είναι ίσος με μηδέν. Δηλαδή θα ισχύει:
![Rendered by QuickLaTeX.com \[\left \{ \begin{matrix} x=0\\ \eta\\ x-1=0\Leftrightarrow x=1 \end{matrix} \right.\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-e0bf973469422918d9d4517961478978_l3.png)
Από τον τρόπο που λύθηκε το προηγούμενο παράδειγμα φαίνεται το ποια μέθοδο πρέπει ν’ ακολουθούμε για να επιλύσουμε μια εξίσωση που έχει βαθμό μεγαλύτερο του πρώτου:
[su_label style=»important»]Βήμα 1ο:[/su_label] Μεταφέρουμε όλους τους όρους στο α’ μέλος έτσι ώστε στο δεύτερο μέλος να είναι ίσο με μηδέν.
[su_label style=»success»]Βήμα 2ο:[/su_label] Μετατρέπουμε σε γινόμενο το α’ μέλος.
[su_label style=»warning»]Βήμα 3ο:[/su_label] Παίρνουμε κάθε παράγοντα του γινομένου ίσο με μηδέν.
[su_label style=»info»]Βήμα 4ο:[/su_label] Λύνουμε κάθε μια από τις εξισώσεις (1ου βαθμού) που προκύπτουν από το προηγούμενο βήμα.


hallo ,δεν μπορώ να κανω εγγραφή και θελω να εχω ενημερωτικο δελτιο
ok
πως λυνετε το παρακατω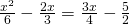
Πολλαπλασιάζουμε τους όρους με το ΕΚΠ των παρονομαστών (το 12):
μετά από τις απλοποιήσεις παίρνουμε:
Επειδή είναι 2ου βαθμού τα φέρνουμε όλα στο 1ο μέλος:
επομένως:
κι έτσι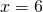 ή
ή 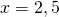
Γεια σας, πώς μπορώ να παραγοντοποιήσω ένα πολυώνυμο τρίτου βαθμού όπως το
Έλενα, αν υποθέσω ότι είσαι μαθήτρια της Γ’ Γυμνασίου η άσκηση που δίνεις είναι αρκετά δύσκολη. Το πως θα καταφέρεις να παραγοντοποιήσεις ένα τέτοιο πολυώνυμο τρίτου βαθμού θα το μάθεις στη Β΄ Λυκείου. Έτσι λοιπόν για την Τρίτη Γυμνασίου κατά τη γνώμη μου αυτή η άσκηση ξεφεύγει από αυτά που είσαι «υποχρεωμένη» να ξέρεις εκτός και αν αυτή αποτελεί υποερώτημα σε άλλη άσκηση που σου δίνει προηγούμενα κάποια σοιχεία για να σε βοηθήσει.
Θα λύσουμε εδώ αυτή την άσκηση αλλά δεν νομίζω ότι αυτή ή κάποια παρόμοια θα μπορούσε να τη λύσει μαθητής της Τρίτης με αυτά που έχει μάθει. Λύνω και θα καταλάβεις το γιατί:
εδώ θα σπάσουμε δύο όρους το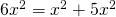 και το
και το 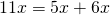
στη συνέχεια τα χωρίζουμε σε ομάδες ανά δύο (ομαδοποίηση)
στο στάδιο που φτάσαμε μετατρέψαμε το πολυώνυμο σε γινόμενο αλλά θα μπορούσαμε να προχωρήσουμε κι άλλο αρκεί να παραγοντοποιήσουμε και το τριώνυμο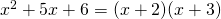 -με όποιον από τους δύο τρόπους έχεις διδαχθεί γιαυτό (άθροισμα και γινόμενο ή με τον τύπο
-με όποιον από τους δύο τρόπους έχεις διδαχθεί γιαυτό (άθροισμα και γινόμενο ή με τον τύπο 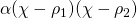 )
)
Τελικά το αρχικό πολυώνυμο γίνεται:
Στα σχόλια λέτε για την επίλυση τριτοβάθμιας.Πώς μπορούμε να βρούμε σε τί πρέπει να σπάσουμε τους όρους με τετράγωνο χ και χ?Ο τρόπος αυτός ισχύει για όλες τις τριτοβάθμιες?
Όχι δεν μπορεί να χρησιμοποιηθεί σε όλες τις περιπτώσεις και γι’ αυτό το λόγο δεν προτείνεται σαν μέθοδος επίλυσης τριτοβάθμιας εξίσωσης.
Χ τετράγωνο συν 4Χ – 5 = μηδέν .Πρεπει να λυθει με παραγοντοποιηση μπορειτε να με βοηθησετε; Ευχαριστω
Θα πρέπει να σπάσεις το 4χ σε 5χ-χ έτσι από 3 όρους θα έχεις 4 όρους και θα κάνεις ομαδοποίηση.
άρα ή χ-1=0 ή χ+5=0 οπότε ή χ=1 ή χ=-5