Αφού είδαμε θεωρητικά το πως μπορούμε να βρούμε τις λύσεις μιας δευτεροβάθμιας εξίσωσης, καλό θα ήταν να το εφαρμόσουμε και στην πράξη
Άσκηση1
Να βρείτε τους φυσικούς αριθμούς χ που ικανοποιούν τη σχέση ![]()
[gn_spoiler title=»Λύση1″]
θα προσπαθήσουμε να κάνουμε τη σχέση(εξίσωση) που μας έχουν δώσει όσο το δυνατόν πιο απλή ξεκινώντας από το να διώξουμε τους παρονομαστές. Αυτό γίνεται αν πολλαπλασιάσουμε όλους τους όρους με το ΕΚΠ των παρονομαστών 2,3 και 6 που είναι το 6 οπότε προκύπτει:
![]()
![]()
που μετά τις απλοποιήσεις γίνεται:
![]()
προσέξτε ότι όταν ένας αριθμητής αποτελείται από δύο ή περισσότερους όρους είμαστε υποχρεωμένοι να τον βάλουμε σε παρένθεση μετά την απαλοιφή των παρονομαστών.
Τώρα θα διώξουμε τις παρενθέσεις κάνοντας επιμεριστική ιδιότητα και προσέχοντας μη τυχόν και υπάρχει «-» έξω από κάποια παρένθεση γιατί τότε θα πρέπει να αλλάξουμε πρόσημα σε όλους τους όρους που βρίσκονται μέσα στη παρένθεση αυτή. Έτσι έχουμε,
![]()
![]()
Έφυγαν και οι παρενθέσεις και μας μένει τώρα η αναγωγή των όμοιων όρων. Επειδή όμως παρατηρούμε ότι η εξίσωση είναι 2ου βαθμού (αφού υπάρχει ο όρος ![]() ) θα τα μαζέψουμε όλα στο ένα μέλος, έστω στο πρώτο, και μετά θα κάνουμε την αναγωγή.
) θα τα μαζέψουμε όλα στο ένα μέλος, έστω στο πρώτο, και μετά θα κάνουμε την αναγωγή.
![]()
![]()
![]()
Από εδώ και κάτω θα ακολουθήσουμε τη διαδικασία που είδαμε στο προηγούμενο άρθρο. Πιο συγκεκριμένα ,
- Ξεκαθαρίζουμε ποιοι αριθμοί παίζουν το ρόλο των α, β και γ

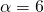 ,
, 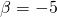 και
και 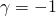
- Υπολογίζουμε τη Διακρίνουσα
![Rendered by QuickLaTeX.com \[\Delta=\beta^2-4\alpha\gamma\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-5d415ece8e5ba7b1aecd03b1a3fc7504_l3.png)
![Rendered by QuickLaTeX.com \[\Delta=(-5)^2-4(+6)(-1)\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-0f5d4bc83b2b9f8041e246c0a65c1b84_l3.png)
![Rendered by QuickLaTeX.com \[\Delta=25+24=49\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-ad76ec09ea43ba19347b6a41aff0b936_l3.png)
Αφού η Διακρίνουσα μας προέκυψε θετική, γνωρίζουμε ότι η εξίσωση θα έχει 2 διαφορετικές λύσεις τις οποίες και θα υπολογίσουμε από τους γνωστούς τύπους
- Υπολογίζουμε τις λύσεις
![Rendered by QuickLaTeX.com \[\chi_1,\chi_2=\frac{-\beta\pm\sqrt{\Delta}}{2\alpha}\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-228906b51cff6fcc77b65938cfdd7a20_l3.png)
![Rendered by QuickLaTeX.com \[\chi_1,\chi_2=\frac{-(-5)\pm\sqrt{49}}{2(+6)}\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-d56d668877cb646783f3ec9c478574fa_l3.png)
![Rendered by QuickLaTeX.com \[\chi_1,\chi_2=\frac{5\pm7}{12}\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-7147163aaedd0c2c48544b2a5b4da978_l3.png)
άρα
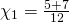 ή
ή 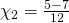
επομένως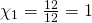 ή
ή 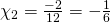
Έτσι λοιπόν καταλήξαμε στο ότι η εξίσωση ![]() έχει λύση τον αριθμό 1 ή τον -1/6. Αλλά ο αριθμός -1/6 δεν είναι φυσικός κι επομένως δεν μπορούμε να τον συμπεριλάβουμε στην απάντησή μας η οποία θα πρέπει να είναι:
έχει λύση τον αριθμό 1 ή τον -1/6. Αλλά ο αριθμός -1/6 δεν είναι φυσικός κι επομένως δεν μπορούμε να τον συμπεριλάβουμε στην απάντησή μας η οποία θα πρέπει να είναι:
Ο φυσικός αριθμός που ικανοποιεί τη σχέση ![]() είναι ο αριθμός 1.
είναι ο αριθμός 1.
[/gn_spoiler]
Άσκηση2
Να υπολογιστεί η υποτείνουσα ορθογωνίου τριγώνου που οι κάθετες πλευρές του είναι ρίζες της εξίσωσης ![]()
[gn_spoiler title=»Λύση2″]
Πρώτα απ’ όλα θα βρούμε τις ρίζες (λύσεις) της δευτεροβάθμιας εξίσωσης
![]()
![]()
![]() άρα
άρα
![]()
αφού η διακρίνουσα είναι ίση με 0 η εξίσωσή μας έχει δύο ίσες λύσεις τις
![]()
.
Πάμε τώρα στο ορθογώνιο τρίγωνο για το οποίο γνωρίζουμε το μήκος των κάθετων πλευρών του ότι είναι 1 και 1 (είναι ισοσκελές) και θέλουμε να βρούμε το μήκος της υποτείνουσάς του. Για το λόγο αυτό χρησιμοποιούμε το Πυθαγόρειο θεώρημα.
Πράγματι έστω x η υποτείνουσα, τότε έχουμε:
![]()
![]()
κι έτσι
![]()
.
[/gn_spoiler]


θα ηθελα να με βοηθεσετε με τις εξης εξισωσεις
αχ+αy+βχ+βy=
Αυτό που μου έχεις γράψει Κατερίνα δεν είναι εξίσωση. Υποθέτω ότι είσαι στην Τρίτη τάξη και θέλεις να κάνεις γινόμενο την παράσταση αχ+αψ+βχ+βψ.
Για να μπορέσεις να καταλάβεις τον τρόπο θα πρέπει να διαβάσεις αυτό:Παραγοντοποίηση και μάλιστα η συγκεκριμένη άσκηση λύνεται με τη μέθοδο της ομαδοποίησης που θα δεις στο λινκ που σου έγραψα. Η λύση της είναι:
αχ+αψ+βχ+βψ=(αχ+αψ)+(βχ+βψ)=α(χ+ψ)+β(χ+ψ)=(χ+ψ)(α+β)
τι να κανω με εξισωσεις που δεν θελω να λυθουν με Διακρινουσα…υπαρχουν καποια βηματα για να ακολουθησω ?
Κάποιες ειδικές περιπτώσεις μπορούν να λυθούν και με άλλο τρόπο, γενικά όμως να ξέρεις ότι μόνο με τη διακρίνουσα μπορείς να λύσεις οποιαδήποτε εξίσωση δεύτερου βαθμού.
Θα ηθελα να με βοηθήσετε με την λυση της παρακατω εξίσωσης 2ου βαθμού: (x-2)(x*x+5x+4)=0
*x υψωμένο στο τετράγωνο
Τάνια, η εξίσωση που έχεις είναι 3ου βαθμού. Είναι γινόμενο που αποτελείται από δύο παράγοντες τον χ-2 και τον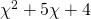 . Στην περίπτωση που έχουμε ένα γινόμενο ίσο με το μηδέν όπως ακριβώς και στην άσκησή σου λύνουμε δύο εξισώσεις, τη μια φορά λύνουμε την εξίσωση στην οποία έχουμε θέσει τον ένα παράγοντα του γινομένου ίσο με το μηδέν και μετά λύνουμε άλλη εξίσωση που έχουμε θέσει τον άλλο παράγοντα ίσο με το μηδέν. Στη δική σου άσκηση λοιπόν θα έχουμε:
. Στην περίπτωση που έχουμε ένα γινόμενο ίσο με το μηδέν όπως ακριβώς και στην άσκησή σου λύνουμε δύο εξισώσεις, τη μια φορά λύνουμε την εξίσωση στην οποία έχουμε θέσει τον ένα παράγοντα του γινομένου ίσο με το μηδέν και μετά λύνουμε άλλη εξίσωση που έχουμε θέσει τον άλλο παράγοντα ίσο με το μηδέν. Στη δική σου άσκηση λοιπόν θα έχουμε:
οπότε λύνουμε την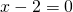 άρα x=2 και την
άρα x=2 και την 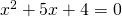 (με την βοήθεια των τύπων) με
(με την βοήθεια των τύπων) με 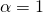
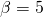
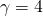 και
και 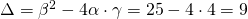 οπότε
οπότε
Τελικά η εξίσωσή σου είχε τρεις λύσεις τους αριθμούς -1, -4, και 2.