Λύκειο Γ΄

ΑΛΓΕΒΡΑ Α΄ ΛΥΚΕΙΟΥ

Όταν μας δίνεται ο τύπος μιας συνάρτησης στην ουσία μας δίνεται μια σχέση (ισότητα) που μας δείχνει τον τρόπο που συνδέονται μεταξύ τους τα x (=πρότυπα) με τα y (ή αλλιώς f(x)-εικόνες). Έτσι έχουμε τη δυνατότητα όταν γνωρίζουμε το x να μπορούμε να υπολογίσουμε την εικόνα του αλλά και το αντίστροφο όταν μας δίνουν το y μπορούμε εμείς να βρούμε το x. Ας πάρουμε για παράδειγμα τη συνάρτηση f με τύπο f(x)=4-x². Για να βρω την εικόνα του 1 δεν έχω παρά να βάλω όπου x τον αριθμό 1 και να υπολογίσω το y. Έτσι θα έχω f(1)=4-1²=3, δηλαδή η εικόνα του 1 είναι ο αριθμός 3. Αυτό μου δίνει και μια επιπλέον πληροφορία ότι η γραφική παράσταση της συνάρτησης f διέρχεται από το σημείο με συντεταγμένες (1,3). Αν τώρα μας ρωτήσουν ποιος αριθμός έχει εικόνα το -12 θα πρέπει εμείς να πάμε και πάλι στον τύπο της συνάρτησης και να βάλουμε όπου y (ή f(x) – το ίδιο είναι) τον αριθμό -12 και από τη σχέση αυτή να υπολογίσουμε το x. Ας το δούμε,

-12=4-x² άρα 0=16-x² δηλαδή (4-x)(4+x)=0 οπότε x=4 ή x= -4. Απαντάμε λοιπόν ότι οι αριθμοί -4 , 4 έχουν εικόνα τον -12. Πράγμα που σημαίνει ακόμη ότι η γραφική παράσταση της συνάρτησης f (συμβολίζεται με C_f) περνάει από τα σημεία (-4,-12) και (4,-12). Τελειώσαμε με την εισαγωγή πάμε τώρα στο θέμα μας.

Θέλουμε να βρούμε τα σημεία που η γραφική παράσταση μιας συνάρτησης τέμνει τον άξονα x’x γνωρίζουμε όμως ότι όλα τα σημεία που βρίσκονται πάνω στον άξονα αυτό έχουν τεταγμένη μηδέν (y=0). Το ίδιο θα ισχύει και με το σημείο που ψάχνουμε άρα αρκεί να βάλουμε στον τύπο της συνάρτησης μας y=0 και να υπολογίσουμε το x. Ας χρησιμοποιήσουμε πάλι την ίδια συνάρτηση που χρησιμοποιήσαμε και πιο πάνω y=4-x² η οποία για y=0 γίνεται 0=4-x² δηλαδή 0=(2-x)(2+x) απ’ όπου προκύπτει x=-2 ή x=2. Επομένως γνωρίζουμε τώρα ότι η f τέμνει τον x’x στα σημεία με συντεταγμένες (-2,0) και (2,0)
Για να βρούμε το σημείο(αν υπάρχει θα είναι ένα και μοναδικό) που η γραφική παράσταση μιας συνάρτησης τέμνει τον άξονα y’y αρκεί να σκεφτούμε ότι όλα τα σημεία του άξονα αυτού έχουν τετμημένη ίση με μηδέν (x=0). Έτσι λοιπόν θα βάλουμε κι εμείς στον τύπο της συνάρτησης όπου x το αριθμό 0 και θα βρούμε πολύ εύκολα το y. Στην y=4-x² για x=0 παίρνω y=4 και γνωρίζω πλέον ότι η f τέμνει τον y’y στο σημείο με συντεταγμένες (0,4).

Μπορούμε τώρα να καταλήξουμε στο παρακάτω συμπέρασμα:

[su_box color=»#0997FC» title=»Τομές γραφικής παράστασης με τους άξονες»][su_list style=»idea»]

Για να βρω που τέμνει η γραφική παράσταση της f

τον x’x, βάζω στον τύπο της f y=0
τον y’y, βάζω στον τύπο της f x=0

[/su_list][/su_box]

Ας δούμε και μερικά παραδειγματάκια τα οποία σας προτείνω να λύσετε μόνοι σας και στη συνέχεια να κάνετε κλικ στη «Λύση» για να τσεκάρετε αυτό που βρήκατε.

Άσκηση 1:

Να βρείτε σε ποιο σημείο τέμνει η

$f(x)=\frac{x^3-1}{2x^5+3x-1}$

τον άξονα y’y
[wpspoiler name=»Λύση»]

Η f αν τέμνει τον y’y θα τον τέμνει στο σημείο με συντεταγμένες (0,f(0)). Αρκεί λοιπόν να βρούμε το f(0). Βάζουμε x=0 και έχουμε

$f(0)=\frac{0^3-1}{2\cdot 0^5+3\cdot 0-1}=\frac{-1}{-1}=1$

Επομένως το σημείο είναι το (0,1)

Παρατήρηση: Μια συνάρτηση δεν είναι υποχρεωτικό να τέμνει τον άξονα y’y αυτό μπορεί να συμβαίνει για παράδειγμα σε μια συνάρτηση που το 0 δεν θα ανήκει στο πεδίο ορισμού της και κατά συνέπεια δεν θα υπάρχει το f(0) π.χ. η g(x)=1/x. Αν στο πεδίο ορισμού της συνάρτησης υπάρχει το 0 τότε μπορώ να βρω την εικόνα του άρα και το σημείο που τέμνει αυτή τον y’y. Το σημείο αυτό όμως θα είναι μοναδικό γιατί δεν γίνεται να δώσω στο x την τιμή 0 και να πάρω περισσότερα από ένα αποτελέσματα άλλωστε το λέει ξεκάθαρα και ο ορισμός της συνάρτησης ότι «σε κάθε x από το πεδίο ορισμού αντιστοιχεί ένα και μόνο y». Έτσι λοιπόν η γραφική παράσταση μιας συνάρτησης μπορεί να τέμνει τον y’y το πολύ σε ένα σημείο.

[/wpspoiler]

Άσκηση 2:

Αν η συνάρτηση

$f(x)=\frac{x^3-k}{2x^5+3x-3k+4}$

τέμνει τον y’y σε σημείο με τεταγμένη 1 να βρείτε το k.

[wpspoiler name=»Λύση»]Το σημείο που η f τέμνει τον y’y έχει συντεταγμένες (0,f(0)). Η άσκηση μας δίνει τη πληροφορία ότι το σημείο αυτό είναι το (0,1) άρα είναι «υποχρεωτικό» να ισχύει

$f(0)=1\Leftrightarrow$

$\frac{0^3-k}{2\cdot 0^5+3\cdot 0 -3k+4}=1\Leftrightarrow$

$\frac{-k}{-3k+4}=1\Leftrightarrow$

$-k=-3k+4\Leftrightarrow$

$3k-k=4\Leftrightarrow 2k=4\Leftrightarrow k=2$

[/wpspoiler]

Άσκηση 3:

Να βρείτε τα σημεία τομής των γραφικών παραστάσεων των συναρτήσεων

$f(x)=\frac{x^2+x+2}{x-1}$

και

$g(x)=\frac{|4x-12|-8}{x}$

με τους άξονες.

[wpspoiler name=»Λύση»]

Για την f έχουμε
Πεδίο ορισμού:
$\mathbb{R}-\{1\}$

γιατί το x δεν μπορεί να πάρει την τιμή 1 αφού μηδενίζει τον παρονομαστή (x-1=0 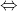$\Leftrightarrow$ x=1)
Τομή με τον y’y: Βάζω x=0 και παίρνω
$f(0)=\frac{0^2+0+2}{0-1}=-2$

άρα τέμνει τον y’y στο (0,-2)
Τομές με τον x’x: Βάζω y=0 και παίρνω
$\frac{x^2+x+2}{x-1}=0\Leftrightarrow x^2+x+2=0$

η εξίσωση αυτή είναι δεύτερου βαθμού με διακρίνουσα αρνητική (Δ=1²-4^.1^.2=-7) επομένως δεν έχει λύσεις πράγμα που σημαίνει ότι η γραφική παράσταση της f δεν τέμνει τον x’x.
Παρατήρηση: Η εξίσωση f(x)=0 είναι μια εξίσωση με άγνωστο το x και το πόσες λύσεις θα έχει εξαρτάται από τη μορφή που θα έχει ο τύπος της συνάρτησης μπορεί να είναι αδύνατη όπως αυτή που είδαμε μόλις τώρα και η C_f να μην τέμνει τον x’x αλλά μπορεί να έχει μια, δύο, τρεις ή και άπειρες λύσεις οπότε να τέμνει τον x’x σε δύο, τρία ή και άπειρα σημεία.
Για την g έχουμε
Πεδίο ορισμού:
$\mathbb{R}-\{0\}$

γιατί το x είναι παρονομαστής και δεν μπορεί να μηδενίζεται
Τομή με τον y’y: Βάζω x=0 ???? Προφανώς η C_g δεν τέμνει τον άξονα των y αφού δεν υπάρχει το g(0)
Τομές με τον x’x: Βάζω y=0 και λύνω την εξίσωση
$g(x)=0\Leftrightarrow$

$\frac{|4x-12|-8}{x}=0\Leftrightarrow$

$|4x-12|-8=0\Leftrightarrow$

$|4x-12|=8\Leftrightarrow$

$\left\{\begin{matrix}4x-12=8\\ \eta \\4x-12=-8 \end{matrix}\Leftrightarrow \left\{\begin{matrix}4x=20\Leftrightarrow x=5\\ \eta \\4x=4\Leftrightarrow x=1\end{matrix}$

επομένως η γραφική παράσταση της g τέμνει τον άξονα x’x στα σημεία (1,0) , (5,0)

[/wpspoiler]

Άσκηση 4:

Αν γνωρίζουμε ότι η συνάρτηση

$f(x)=ax^2+bx+c$

τέμνει τον y’y στο σημείο με τεταγμένη 6 και τον x’x στα σημεία με τετμημένες 2 και 3 να βρεθούν τα a,b και c.

[wpspoiler name=»Λύση»]

Επειδή η f τέμνει τον y’y στο (0,6) θα πρέπει να ισχύει

$f(0)=6\Leftrightarrow a0^2+b0+c=6\Leftrightarrow c=6$

Τώρα η συνάρτηση μας παίρνει τη μορφή

$f(x)=ax^2+bx+6$

γνωρίζουμε όμως ότι τέμνει και τον x’x στα (2,0) και (3,0) επομένως θα ισχύει

$\left\{\begin{matrix}f(2)=0\\ \kappa\alpha\iota\\f(3)=0\end{matrix} \Leftrightarrow$ $\left\{\begin{matrix}4a+2b+6=0\\ \kappa\alpha\iota\\9a+3b+6=0\end{matrix}\Leftrightarrow$ $\left\{\begin{matrix}2a+b+3=0\\ \kappa\alpha\iota\\3a+b+2=0\end{matrix}\Leftrightarrow$

$\left\{\begin{matrix}2a+b=-3\\ \kappa\alpha\iota\\3a+b=-2\end{matrix}\Leftrightarrow$ $\left\{\begin{matrix}b=-2a-3\\ \kappa\alpha\iota\\3a+(-2a-3)=-2\end{matrix}\Leftrightarrow$ $\left\\{begin{matrix}b=-2a-3\\ \kappa\alpha\iota\\a-3=-2\end{matrix}\Leftrightarrow$

$\left\{\begin{matrix}b=-2a-3\\ \kappa\alpha\iota\\a=1\end{matrix}\Leftrightarrow$ $\left\{\begin{matrix}b=-2\cdot 1-3\\ \kappa\alpha\iota\\a=1\end{matrix}\Leftrightarrow$ $\left\{\begin{matrix}b=-5\\ \kappa\alpha\iota\\a=1\end{matrix}$

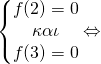
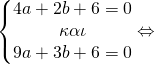
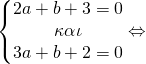
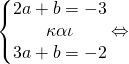
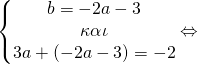
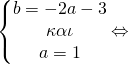
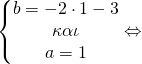
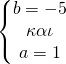
Έτσι μετά τη λύση του συστήματος βρήκαμε a=1, b=-5, c=6 οπότε και η f είναι η

$f(x)=x^2-5x+6$

[/wpspoiler]

Κατηγορία: Λύκειο Γ΄

Θέλω να μάθω…πως βρίσκουμε τα σημεία που η γραφική παράσταση μιας συνάρτησης τέμνει τους άξονες

Άσκηση 1:

Άσκηση 2:

Άσκηση 3:

Άσκηση 4: