Μήνας: Νοεμβρίου 2012
Πρώτοι & Σύνθετοι Αριθμοί – Βιντεομάθημα
Διαιρέτες Μ.Κ.Δ. – Βιντεομάθημα
Πολλαπλάσια Ε.Κ.Π. – Βιντεομάθημα
Ιδιότητες Κλασμάτων
Κατ’ αρχάς θα δεχτούμε ότι το κλάσμα ![]() παριστάνει το πηλίκο της διαίρεσης
παριστάνει το πηλίκο της διαίρεσης ![]() . Έτσι λοιπόν έχουμε ότι
. Έτσι λοιπόν έχουμε ότι ![]() . Μέσα από αυτό τον ορισμό προκύπτουν εύκολα οι παρακάτω ιδιότητες των κλασμάτων:
. Μέσα από αυτό τον ορισμό προκύπτουν εύκολα οι παρακάτω ιδιότητες των κλασμάτων:
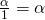 αφού
αφού 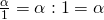
Σύμφωνα με αυτή την ιδιότητα κάθε αριθμός μπορεί να γραφεί σαν κλάσμα, αρκεί να του βάλουμε παρονομαστή το 1.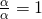 αφού
αφού 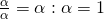
Εδώ βλέπουμε ότι όταν σε ένα κλάσμα ο αριθμητής και ο παρονομαστής είναι ίσοι, τότε το κλάσμα είναι ίσο με 1. Και αντίστροφα αν δούμε ότι συμβαίνει αυτό: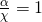 ή αυτό:
ή αυτό: 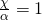 τότε αμέσως συμπεραίνουμε ότι:
τότε αμέσως συμπεραίνουμε ότι: 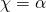 Δηλαδή ισχύει:
Δηλαδή ισχύει:  και
και  και λίγο πιο συνοπτικά:
και λίγο πιο συνοπτικά: 
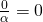 αφού
αφού 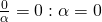
Από αυτή την ιδιότητα έχουμε ότι ένα κλάσμα είναι ίσο με το 0 αν και μόνο αν ο αριθμητής του είναι το 0. Δηλαδή ισχύει: Παρατήρηση: Ο παρονομαστής του κλάσματος δεν μπορεί να είναι μηδέν αφού όπως είδαμε και στην Ευκλείδεια Διαίρεση δεν επιτρέπεται διαίρεση με το 0.
Παρατήρηση: Ο παρονομαστής του κλάσματος δεν μπορεί να είναι μηδέν αφού όπως είδαμε και στην Ευκλείδεια Διαίρεση δεν επιτρέπεται διαίρεση με το 0.
Συγκεντρωτικά:
| Ιδιότητες Κλασμάτων |
|
|
|
|
|
|
|
|
![]()
![]()
Σύγκριση Κλασμάτων
Μαθαίνουμε πότε τα κλάσματα λέγονται ομώνυμα και πότε ετερώνυμα.
Μαθαίνουμε να μετατρέπουμε τα ετερώνυμα κλάσματα σε ομώνυμα, να συγκρίνουμε κλάσματα για να δούμε αν είναι ίσα και στην περίπτωση που δεν είναι να ξέρουμε ποιο είναι μεγαλύτερο.
Ομώνυμα λέγονται δύο ή περισσότερα κλάσματα όταν έχουν τον ίδιο παρονομαστή.
Ετερώνυμα λέγονται δύο ή περισσότερα κλάσματα όταν δεν έχουν ίδιους παρονομαστές.
Πως μπορούμε να μετατρέψουμε ετερώνυμα κλάσματα σε ομώνυμα;
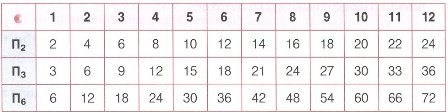
i. Βρίσκουμε το ΕΚΠ των παρονομαστών:
![]() , ΕΚΠ(4,6,12)=12
, ΕΚΠ(4,6,12)=12
ii. Διαιρούμε το ΕΚΠ με κάθε παρονομαστή:
12:4=3, 12:6=2 και 12:12=1
iii. Με τον αριθμό που προκύπτει πολλαπλασιάζουμε τους όρους κάθε κλάσματος:
![]()
![]()
![]()
κι έτσι προκύπτουν ισοδύναμα με τα αρχικά κλάσματα που είναι πλέον ομώνυμα με παρονομαστή το ΕΚΠ των παρονομαστών.
Γιατί να μετατρέψουμε ετερώνυμα κλάσματα σε ομώνυμα;
πρώτον, όπως θα δούμε αμέσως πιο κάτω, για να μπορέσουμε να τα συγκρίνουμε και δεύτερον, όπως θα δούμε στην επόμενη ενότητα, για να τα προσθέσουμε ή για να τα αφαιρέσουμε.
Σύγκριση κλασμάτων:
Πως ελέγχουμε αν δύο κλάματα είναι ισοδύναμα;
α΄ τρόπος: Αν έχουμε δύο κλάσματα και θέλουμε να δούμε αν αυτά είναι ίσα ή όχι ελέγχουμε αν είναι ίσα τα «χιαστί» γινόμενα. Δηλαδή πολλαπλασιάζουμε τον αριθμητή του ενός με τον παρονομαστή του άλλου. Αυτό το κάνουμε και για τα δύο κλάσματα κι αν τα γινόμενα που προκύψουν είναι ίσα, τότε και τα κλάσματα είναι ίσα.
‘Έστω ότι έχουμε να ελέγξουμε την αλήθεια της παρακάτω πρότασης:![]() κάνουμε
κάνουμε ![]() και
και ![]() και βλέπουμε ότι τα κλάσματα που μας έδωσαν είναι πράγματι ίσα.
και βλέπουμε ότι τα κλάσματα που μας έδωσαν είναι πράγματι ίσα.
β΄ τρόπος: Κάνουμε τα κλάσματα ομώνυμα.
Αυτός ο τρόπος προσφέρεται στη περίπτωση που έχουμε να ελέγξουμε αν είναι ίσα περισσότερα από δύο κλάσματα. Ακόμη με αυτόν τον τρόπο όχι μόνο βλέπουμε αν τα κλάσμα είναι ίσα αλλά και στην περίπτωση που αυτά είναι άνισα μπορούμε να καταλάβουμε ποιο είναι μικρότερο και ποιο μεγαλύτερο.
Πως συγκρίνουμε δύο ή περισσότερα κλάσματα;
Αν έχουν ίδιους παρονομαστές (ομώνυμα), τότε κοιτάμε τους αριθμητές και προφανώς μεγαλύτερο είναι αυτό που έχει τον πιο μεγάλο αριθμητή.
π.χ. ![]()
Αν έχουν διαφορετικούς παρονομαστές (ετερώνυμα), τότε τα μετατρέπουμε σε ομώνυμα κι εφαρμόζουμε το προηγούμενο.
Ισοδύναμα Κλάσματα
 Αν υποθέσουμε ότι έχουμε μία πίτσα που την κόβουμε σε 8 ίσα κομμάτια και από αυτά παίρνουμε τα 4, τότε έχουμε πάρει τα
Αν υποθέσουμε ότι έχουμε μία πίτσα που την κόβουμε σε 8 ίσα κομμάτια και από αυτά παίρνουμε τα 4, τότε έχουμε πάρει τα ![]() της πίτσας.
της πίτσας.
Αν αυτή τη κόβαμε σε 4 ίσα κομμάτια και από αυτά παίρναμε τα 2, τότε θα είχαμε τα ![]() της πίτσας.
της πίτσας.
Και στις δύο περιπτώσεις όμως θα είχαμε πάρει τη μισή πίτσα. Έτσι παρότι τα κλάσματα ![]() και
και ![]() φαίνονται διαφορετικά στην πραγματικότητα δεν είναι αφού εκφράζουν και τα δύο το ίδιο μέρος της πίτσας. Τα κλάσματα αυτά είναι λοιπόν ίσα ή ισοδύναμα.
φαίνονται διαφορετικά στην πραγματικότητα δεν είναι αφού εκφράζουν και τα δύο το ίδιο μέρος της πίτσας. Τα κλάσματα αυτά είναι λοιπόν ίσα ή ισοδύναμα.
[important]
Γενικότερα,
Ισοδύναμα (ή ίσα) λέγονται δύο ή περισσότερα κλάσματα όταν εκφράζουν το ίδιο μέρος (τμήμα) ενός μεγέθους.
[/important]
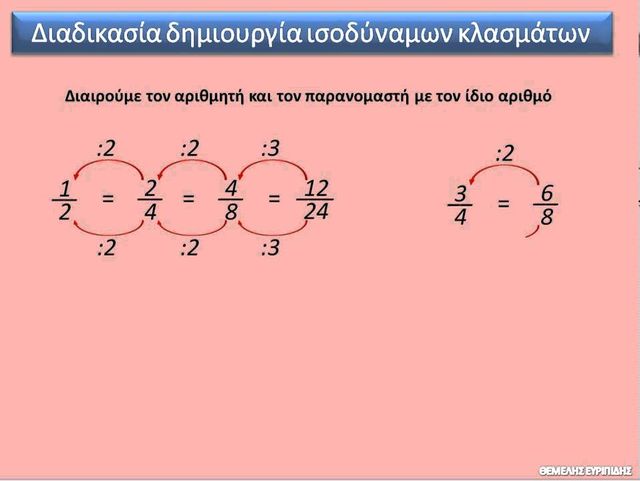
Να δούμε όμως όταν μας δώσουν ένα κλάσμα,πως μπορούμε εμείς να φτιάξουμε ένα ή και περισσότερα άλλα κλάσματα ισοδύναμα με αυτό. Αν παρατηρήσουμε τα κλάσματα του προηγούμενου παραδείγματος θα δούμε ότι για να πάμε από το ![]() στο
στο ![]() αρκεί να πολλαπλασιάσουμε και τους δύο όρους του
αρκεί να πολλαπλασιάσουμε και τους δύο όρους του ![]() με τον αριθμό 2, και αντίστροφα για να πάμε από το
με τον αριθμό 2, και αντίστροφα για να πάμε από το ![]() στο
στο ![]() πρέπει να διαιρέσουμε τους όρους με το 2. Έτσι λοιπόν συμπεραίνουμε ότι:
πρέπει να διαιρέσουμε τους όρους με το 2. Έτσι λοιπόν συμπεραίνουμε ότι:
Για να φτιάξεις κλάσματα ισοδύναμα με κάποιο δοσμένο κλάσμα αρκεί:
ή να πολλαπλασιάσεις τους όρους του κλάσματος με τον ίδιο αριθμό ( π.χ. ![]() )
)
ή να διαιρέσεις τους όρους του κλάματος με τον ίδιο αριθμό ( ![]() ).
).
Ισχύουν λοιπόν τα εξής:
και
![]()
![]()
Όταν διαιρούμαι τους όρους ενός κλάσματος με κάποιον κοινό διαιρέτη τους, προκύπτει ένα νέο κλάσμα ισοδύναμο με το αρχικό αλλά με μικρότερους όρους. Όπως και στο προηγούμενο παράδειγμα από το κλάσμα ![]() διαιρώντας και τους δύο όρους με το 10 καταλήξαμε στο πιο απλό
διαιρώντας και τους δύο όρους με το 10 καταλήξαμε στο πιο απλό ![]() . Τα δύο αυτά κλάσματα είναι ίσα αλλά το
. Τα δύο αυτά κλάσματα είναι ίσα αλλά το ![]() έχει μικρότερους όρους από το
έχει μικρότερους όρους από το ![]() . Η παραπάνω διαδικασία ονομάζεται απλοποίηση κλάσματος.
. Η παραπάνω διαδικασία ονομάζεται απλοποίηση κλάσματος.
[important]
Δηλαδή:
Απλοποίηση κλάσματος ονομάζουμε τη διαδικασία κατά την οποία βρίσκουμε ένα κλάσμα ίσο με το αρχικό αλλά με μικρότερους όρους.
[/important]
Για να κάνουμε απλοποίηση πρέπει να διαιρέσουμε τους όρους του κλάσματος με κάποιο κοινό διαιρέτη του αριθμητή και του παρονομαστή (π.χ ![]() ). Αν όμως χρησιμοποιήσουμε τον ΜΚΔ
). Αν όμως χρησιμοποιήσουμε τον ΜΚΔ
του αριθμητή και παρονομαστή θα πετύχουμε καλύτερο αποτέλεσμα (π.χ. ΜΚΔ(6,12)=6, άρα ![]() ).
).
[important]
Όταν ένα κλάσμα δεν απλοποιείται καλείται ανάγωγο.
[/important]
Π.χ. τα κλάσματα ![]() ,
, ![]() και είναι ανάγωγα.
και είναι ανάγωγα.
Η έννοια του κλάσματος
 Από ένα τμήμα 25 μαθητών επιλέγουμε 4 για την παρέλαση. Έχουμε λοιπόν πάρει τους 4 από τους 25. Αυτό θα μπορούσαμε να το συμβολίσουμε και ως
Από ένα τμήμα 25 μαθητών επιλέγουμε 4 για την παρέλαση. Έχουμε λοιπόν πάρει τους 4 από τους 25. Αυτό θα μπορούσαμε να το συμβολίσουμε και ως ![]() και το διαβάζουμε «4 από τους 25» ή «4 προς 25» ή και «τέσσερα εικοστά πέμπτα». Ο συμβολισμός αυτός λέγεται κλάσμα (που σημαίνει κομμάτι και δηλώνει ένα μέρος από ένα σύνολο).
και το διαβάζουμε «4 από τους 25» ή «4 προς 25» ή και «τέσσερα εικοστά πέμπτα». Ο συμβολισμός αυτός λέγεται κλάσμα (που σημαίνει κομμάτι και δηλώνει ένα μέρος από ένα σύνολο).
Αν κόψουμε μία πίτσα σε 8 ίσα κομμάτια και από αυτά πάρουμε τα 2, τότε λέμε ότι έχουμε τα 2 από τα 8, δηλαδή έχουμε τα ![]() της πίτσας.
της πίτσας.
Και γενικότερα:
Όταν έχουμε ένα μέγεθος και το χωρίζουμε σε ν ίσα μέρη, τότε το καθένα από αυτά είναι ίσο με το «ένα νιοστό του μεγέθους». Ο συμβολισμός σε αυτή τη περίπτωση είναι ![]() . Αν πάρουμε κ από αυτά τα ίσα κομμάτια τότε λέμε πως έχουμε πάρει τα «κάπα από τα νι» ή συμβολικά
. Αν πάρουμε κ από αυτά τα ίσα κομμάτια τότε λέμε πως έχουμε πάρει τα «κάπα από τα νι» ή συμβολικά ![]() (διαβάζεται κ προς ν).Στην περίπτωση που έχουμε μια ομάδα από ν όμοια αντικείμενα και πάρουμε κ από αυτά , τότε και πάλι λέμε ότι έχουμε πάρει τα «κάπα από τα νι» ή τα « κάπα νιοστά». Ο συμβολισμός και πάλι είναι
(διαβάζεται κ προς ν).Στην περίπτωση που έχουμε μια ομάδα από ν όμοια αντικείμενα και πάρουμε κ από αυτά , τότε και πάλι λέμε ότι έχουμε πάρει τα «κάπα από τα νι» ή τα « κάπα νιοστά». Ο συμβολισμός και πάλι είναι ![]() .
.
Το σύμβολο ![]() λέγεται κλάσμα. Ο αριθμός κ λέγεται αριθμητής ενώ ο αριθμός ν παρονομαστής. Ο αριθμητής και ο παρονομαστής λέγονται όροι του κλάσματος.
λέγεται κλάσμα. Ο αριθμός κ λέγεται αριθμητής ενώ ο αριθμός ν παρονομαστής. Ο αριθμητής και ο παρονομαστής λέγονται όροι του κλάσματος.
Γενικότερα,
κλάσμα ονομάζουμε το σύμβολο ![]() με
με ![]() .
.
[error]Παρατήρηση: Ο παρονομαστής β δεν μπορεί να είναι 0 αφού δεν είναι δυνατό ένα μέγεθος να το χωρίσουμε σε 0 κομμάτια.[/error]
Κριτήρια ή Χαρακτήρες Διαιρετότητας
Κριτήρια (ή χαρακτήρες ) διαιρετότητας ονομάζονται οι κανόνες με τους οποίους μπορούμε να συμπεράνουμε αν ένας αριθμός διαιρείται με κάποιον άλλο χωρίς να χρειαστεί να κάνουμε τη διαίρεση.

Κριτήρια (ή χαρακτήρες ) διαιρετότητας ονομάζονται οι κανόνες με τους οποίους μπορούμε να συμπεράνουμε αν ένας αριθμός διαιρείται με κάποιον άλλο χωρίς να χρειαστεί να κάνουμε τη διαίρεση.
| Διαίρεση με το | όταν |
| 2 | λήγει σε 0,2,4,6,8 |
| 5 | λήγει σε 0,5 |
| 10 | λήγει σε 0 |
| 100 | λήγει σε 00 |
| 3 | το μονοψήφιο άθροισμα των ψηφίων του είναι 3 ή 6 ή 9 |
| 9 | το μονοψήφιο άθροισμα των ψηφίων του είναι 9 |
| 4 | το τελευταίο διψήφιο κομμάτι του αριθμού είναι πολλαπλάσιο του 4 |
| 6 | διαιρείται και με το 2 και με το 3 |
| 25 | λήγει σε 00 ή 25 ή 50 ή 75 |
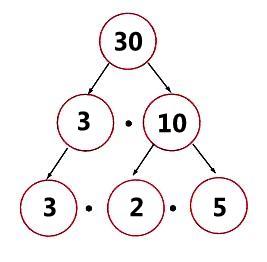
Ανάλυση Αριθμού σε Γινόμενο Πρώτων Παραγόντων
Κάθε φυσικός αριθμός μπορεί να γραφεί σε μορφή γινομένου που ο κάθε παράγοντας να είναι πρώτος αριθμός.(και μάλιστα με μοναδικό τρόπο)
π.χ. το ![]() και το
και το ![]() .
.
Η ανάλυση ενός αριθμού σε γινόμενο πρώτων παραγόντων μας βοηθά στο να βρίσκουμε το Ε.Κ.Π. και τον Μ.Κ.Δ. δύο ή περισσότερων αριθμών.
Αν έχουμε δύο ή περισσότερους αριθμούς σε μορφή γινομένου πρώτων παραγόντων, τότε
Το ΕΚΠ τους είναι ίσο με: το γινόμενο των κοινών και μη κοινών παραγόντων τους με το μεγαλύτερο εκθέτη.
Ο ΜΚΔ τους είναι ίσος με: το γινόμενο των κοινών παραγόντων τους με το μικρότερο εκθέτη.
Παράδειγμα: Αν αναλύσουμε σε γινόμενο πρώτων παραγόντων τους αριθμούς 18 και 24 θα πάρουμε: ![]() και
και ![]() .
.
Επομένως το ΕΚΠ του 18 και του 24 είναι ΕΚΠ(18,24) = ![]() (κοινοί και μη κοινοί παράγοντες με το μεγαλύτερο εκθέτη) και
(κοινοί και μη κοινοί παράγοντες με το μεγαλύτερο εκθέτη) και
ο ΜΚΔ είναι ΜΚΔ(18,24) = ![]() (οι κοινοί παράγοντες με το μικρότερο εκθέτη) .
(οι κοινοί παράγοντες με το μικρότερο εκθέτη) .