Γ΄ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
Εισαγωγή
Το πρώτο πράγμα που πρέπει να συζητήσουμε εδώ είναι το τι είναι το όριο μιας συνάρτησης. Δυστυχώς ή ευτυχώς στα μαθηματικά της γενικής παιδείας δεν μπορούμε να δώσουμε μαθηματικό ορισμό του ορίου, οπότε το μόνο που μας μένει είναι να πούμε «στο περίπου» τι είναι το όριο μιας συνάρτησης σε κάποιο συγκεκριμένο σημείο. Ας το δούμε αυτό καλύτερα με ένα παράδειγμα. Ας υποθέσουμε ότι έχουμε τη συνάρτηση f που έχει τύπο ![]() , το Πεδίο Ορισμού αυτής είναι το
, το Πεδίο Ορισμού αυτής είναι το ![]() (αν δεν θυμάσαι πως βρίσκουμε το Πεδίο Ορισμού μιας συνάρτησης κάνε κλικ εδώ). Στην περίπτωση που θέλουμε να βρούμε την τιμή που παίρνει f όταν το χ πάρει την τιμή 2 δεν έχουμε παρά να βρούμε το f(2) αντικαθιστώντας στον τύπο της f όπου x τον αριθμό 2 και βρίσκουμε
(αν δεν θυμάσαι πως βρίσκουμε το Πεδίο Ορισμού μιας συνάρτησης κάνε κλικ εδώ). Στην περίπτωση που θέλουμε να βρούμε την τιμή που παίρνει f όταν το χ πάρει την τιμή 2 δεν έχουμε παρά να βρούμε το f(2) αντικαθιστώντας στον τύπο της f όπου x τον αριθμό 2 και βρίσκουμε ![]() . Με αυτό τον απλό τρόπο μπορούμε να βρούμε την τιμή της f σε οποιοδήποτε σημείο του Πεδίου Oρισμού της. Αν θέλουμε όμως να δούμε τι τιμή παίρνει η συνάρτησή μας για x=1 αυτό είναι αδύνατο γιατί αφού το 1 δεν ανήκει στο Πεδίο Ορισμού της συνάρτησης δεν έχω το δικαίωμα να βάλω όπου χ το 1.
. Με αυτό τον απλό τρόπο μπορούμε να βρούμε την τιμή της f σε οποιοδήποτε σημείο του Πεδίου Oρισμού της. Αν θέλουμε όμως να δούμε τι τιμή παίρνει η συνάρτησή μας για x=1 αυτό είναι αδύνατο γιατί αφού το 1 δεν ανήκει στο Πεδίο Ορισμού της συνάρτησης δεν έχω το δικαίωμα να βάλω όπου χ το 1.
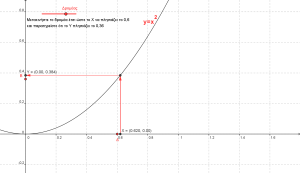
Το μόνο που μπορώ να κάνω είναι να δω το πως «συμπεριφέρεται» η συνάρτηση f όταν το x παίρνει τιμές πάρα πολύ κοντά στο 1. Σε αυτή τη περίπτωση λοιπόν αντί να βάζω x=1, χρησιμοποιώ την έννοια του «ορίου» και γράφω ![]() που σημαίνει ότι το x πλησιάζει (πάρα πολύ κοντά) στον αριθμό 1 και διαβάζεται «το x τείνει – πλησιάζει δηλαδή – το 1». Υποθέτουμε, προς το παρόν, ότι βρήκαμε το όριο και ότι αυτό είναι 2 ( θα δούμε παρακάτω πως υπολογίζεται ) δεν είναι σωστό να γράψουμε f(1)=2 γιατί αυτό σημαίνει ότι στη συνάρτηση f θέσαμε όπου x τον αριθμό 1 και αυτή μας έδωσε ως αποτέλεσμα την τιμή 2. Το σωστό είναι να γράψουμε
που σημαίνει ότι το x πλησιάζει (πάρα πολύ κοντά) στον αριθμό 1 και διαβάζεται «το x τείνει – πλησιάζει δηλαδή – το 1». Υποθέτουμε, προς το παρόν, ότι βρήκαμε το όριο και ότι αυτό είναι 2 ( θα δούμε παρακάτω πως υπολογίζεται ) δεν είναι σωστό να γράψουμε f(1)=2 γιατί αυτό σημαίνει ότι στη συνάρτηση f θέσαμε όπου x τον αριθμό 1 και αυτή μας έδωσε ως αποτέλεσμα την τιμή 2. Το σωστό είναι να γράψουμε ![]() που διαβάζεται «το όριο της συνάρτησης f , όταν το x τείνει στο 1, είναι ο αριθμός 2» και σημαίνει ότι: όταν το x παίρνει τιμές πολύ κοντά στο 1 το f(x) παίρνει τιμές πολύ κοντά στο 2. Επειδή σκοπός του άρθρου αυτού δεν είναι η έννοια του ορίου αλλά ο τρόπος υπολογισμού του ας προχωρήσουμε στο πως μπορούμε να βρούμε το όριο μιας συνάρτησης f όταν το x τείνει σε κάποιον αριθμό a (
που διαβάζεται «το όριο της συνάρτησης f , όταν το x τείνει στο 1, είναι ο αριθμός 2» και σημαίνει ότι: όταν το x παίρνει τιμές πολύ κοντά στο 1 το f(x) παίρνει τιμές πολύ κοντά στο 2. Επειδή σκοπός του άρθρου αυτού δεν είναι η έννοια του ορίου αλλά ο τρόπος υπολογισμού του ας προχωρήσουμε στο πως μπορούμε να βρούμε το όριο μιας συνάρτησης f όταν το x τείνει σε κάποιον αριθμό a (![]() ) και με την προϋπόθεση ότι το x θα μπορεί να πλησιάζει τον αριθμό a. Γιατί δεν μπορούμε να μιλάμε για όριο μιας συνάρτησης έστω g στο 5 αν το Πεδίο Ορισμού της είναι για παράδειγμα το σύνολο
) και με την προϋπόθεση ότι το x θα μπορεί να πλησιάζει τον αριθμό a. Γιατί δεν μπορούμε να μιλάμε για όριο μιας συνάρτησης έστω g στο 5 αν το Πεδίο Ορισμού της είναι για παράδειγμα το σύνολο ![]() αφού το x ανήκει σε αυτό το διάστημα μπορεί να πάρει οποιαδήποτε τιμή μεγαλύτερη του 1 αλλά μικρότερη του 4 πως λοιπόν θα του δώσουμε τιμές κοντά στο 5;
αφού το x ανήκει σε αυτό το διάστημα μπορεί να πάρει οποιαδήποτε τιμή μεγαλύτερη του 1 αλλά μικρότερη του 4 πως λοιπόν θα του δώσουμε τιμές κοντά στο 5;
Υπολογισμός Ορίου
[su_tabs style=1]
[su_tab title=»Η απλή περίπτωση»]
Στην περίπτωση που θέλουμε να υπολογίσουμε το όριο μιας συνάρτησης f όταν το x τείνει σε κάποιο σημείο a , τότε πολύ απλά βρίσκουμε το f(a) αντικαθιστώντας όπου x τον αριθμό a αρκεί:
- να μπορεί, όπως αναφέραμε πιο πάνω, το x να πλησιάζει το a , και
- να μην μηδενίζεται ο παρονομαστής της συνάρτησης
Ας δούμε κάποια παραδείγματα:
- Δίνεται η συνάρτηση
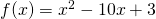 , να βρεθεί το
, να βρεθεί το  .Λύση: Βλέπουμε ότι η f έχει Πεδίο Ορισμού όλο το
.Λύση: Βλέπουμε ότι η f έχει Πεδίο Ορισμού όλο το 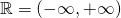 κι επομένως το x μπορεί να πλησιάζει στο 1 οπότε μπορούμε να ξεκινήσουμε τον υπολογισμό του ορίου:
κι επομένως το x μπορεί να πλησιάζει στο 1 οπότε μπορούμε να ξεκινήσουμε τον υπολογισμό του ορίου:
![Rendered by QuickLaTeX.com \[\underset{x\to 1 }{\mathop{\lim }}f(x)=\underset{x\to 1 }{\mathop{\lim }}(x^2-10x+3)=\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-613079e2fff0e19ef903d2209ed2b52a_l3.png)
![Rendered by QuickLaTeX.com \[=1^2-10\cdot 1+3=-6\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-1f401510464e4007779dd36248abe20b_l3.png)
- Για τη συνάρτηση
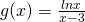 να βρείτε τα όρια
να βρείτε τα όρια 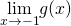 και
και 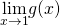 .Λύση: Το πρώτο πράγμα που κάνουμε πάντα είτε το ζητάει η άσκηση είτε όχι είναι να βρούμε το πεδίο ορισμού της συνάρτησης η οποία παρατηρούμε ότι έχει έχει λογάριθμο και πρέπει το περιεχόμενό του να είναι θετικό (άρα πρέπει x>0) και παρονομαστή το x-3 που δεν πρέπει να μηδενίζεται κι επομένως το x δεν μπορεί να πάρει την τιμή 3 καταλήγουμε λοιπόν στο ότι το πεδίο ορισμού της g είναι το
.Λύση: Το πρώτο πράγμα που κάνουμε πάντα είτε το ζητάει η άσκηση είτε όχι είναι να βρούμε το πεδίο ορισμού της συνάρτησης η οποία παρατηρούμε ότι έχει έχει λογάριθμο και πρέπει το περιεχόμενό του να είναι θετικό (άρα πρέπει x>0) και παρονομαστή το x-3 που δεν πρέπει να μηδενίζεται κι επομένως το x δεν μπορεί να πάρει την τιμή 3 καταλήγουμε λοιπόν στο ότι το πεδίο ορισμού της g είναι το 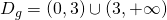 . Όσον αφορά στα όρια τώρα, βλέπουμε ότι το πρώτο από αυτά δεν έχει νόημα αφού το x δεν έχει τη δυνατότητα να «πλησιάζει» το -1 οπότε το αφήνουμε και για να είμαι ειλικρινής δεν πιστεύω ότι θα ζητηθεί ποτέ κάτι τέτοιο. Πάμε τώρα στο δεύτερο όριο το οποίο και θα υπολογίσουμε κανονικότατα
. Όσον αφορά στα όρια τώρα, βλέπουμε ότι το πρώτο από αυτά δεν έχει νόημα αφού το x δεν έχει τη δυνατότητα να «πλησιάζει» το -1 οπότε το αφήνουμε και για να είμαι ειλικρινής δεν πιστεύω ότι θα ζητηθεί ποτέ κάτι τέτοιο. Πάμε τώρα στο δεύτερο όριο το οποίο και θα υπολογίσουμε κανονικότατα
![Rendered by QuickLaTeX.com \[\underset{x\to 1}{\mathop{\lim }}g(x)=\underset{x\to 1}{\mathop{\lim }}\frac{lnx}{x-3}=\frac{ln1}{1-3}=\frac{0}{-2}=0\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-30e6878e453519c0892787595321274b_l3.png)
- Να βρεθεί το όριο
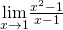
Λύση: Η συνάρτηση της οποίας αναζητάμε το όριο στο 1 είναι η![Rendered by QuickLaTeX.com \[h(x)=\frac{x^2-1}{x-1}\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-ca2eac187f9324a9f90db66551170ff2_l3.png)
. Επειδή η συνάρτηση έχει παρονομαστή το x-1 έχει πεδίο ορισμού το
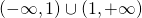 . Παρατηρούμε ότι το 1 δεν ανήκει στο πεδίο ορισμού της συνάρτησης, πράγμα που σημαίνει ότι δεν μπορώ να θέσω x=1, αυτό όμως δεν αποτελεί πρόβλημα αφού το x
. Παρατηρούμε ότι το 1 δεν ανήκει στο πεδίο ορισμού της συνάρτησης, πράγμα που σημαίνει ότι δεν μπορώ να θέσω x=1, αυτό όμως δεν αποτελεί πρόβλημα αφού το x έχει τη δυνατότητα να «προσεγγίσει» το 1 (δηλαδή μπορεί
έχει τη δυνατότητα να «προσεγγίσει» το 1 (δηλαδή μπορεί 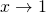 ) κι επομένως θα μπορούσαμε να υπολογίσουμε το όριο αυτό αν δεν είχαμε άλλο πρόβλημα. Και ποιο είναι το πρόβλημα αυτό; Ότι ο αριθμός 1 μηδενίζει τον παρονομαστή μας. Ευτυχώς όμως το 1 μηδενίζει και τον αριθμητή ( το x2-1 ) και αυτό μας λύνει τα χέρια γιατί σημαίνει ότι ο αριθμός 1 είναι ρίζα και του παρονομαστή αλλά και του αριθμητή κι όπως μάθαμε στη Β΄ Λυκείου, στον αριθμητή x2-1 είναι κρυμμένος ο παράγοντας x-1 [wpspoiler name=»διαβάστε εδώ το γιατί» ]όταν ένα πολυώνυμο p(x) μηδενίζεται για x=ρ, τότε θα έχει ρίζα τον αριθμό ρ και συνεπώς θα έχει παράγοντα το x-ρ, πράγμα που σημαίνει ότι το πολυώνυμο αναλύεται σε γινόμενο παραγόντων όπου ο ένας από τους παράγοντές του θα είναι το x-ρ, δηλαδή θα ισχύει p(x)=(x – ρ).π(x) , άρα:
) κι επομένως θα μπορούσαμε να υπολογίσουμε το όριο αυτό αν δεν είχαμε άλλο πρόβλημα. Και ποιο είναι το πρόβλημα αυτό; Ότι ο αριθμός 1 μηδενίζει τον παρονομαστή μας. Ευτυχώς όμως το 1 μηδενίζει και τον αριθμητή ( το x2-1 ) και αυτό μας λύνει τα χέρια γιατί σημαίνει ότι ο αριθμός 1 είναι ρίζα και του παρονομαστή αλλά και του αριθμητή κι όπως μάθαμε στη Β΄ Λυκείου, στον αριθμητή x2-1 είναι κρυμμένος ο παράγοντας x-1 [wpspoiler name=»διαβάστε εδώ το γιατί» ]όταν ένα πολυώνυμο p(x) μηδενίζεται για x=ρ, τότε θα έχει ρίζα τον αριθμό ρ και συνεπώς θα έχει παράγοντα το x-ρ, πράγμα που σημαίνει ότι το πολυώνυμο αναλύεται σε γινόμενο παραγόντων όπου ο ένας από τους παράγοντές του θα είναι το x-ρ, δηλαδή θα ισχύει p(x)=(x – ρ).π(x) , άρα:
![Rendered by QuickLaTeX.com \[P(\rho)=0 \Leftrightarrow P(x)=(x-\rho) \cdot \pi(x)\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-11d9992d557a8f258d8c87b25852e922_l3.png)
[/wpspoiler] Έτσι εμείς αρκεί να τον εμφανίσουμε για να μπορέσουμε να τον εξαφανίσουμε (δηλαδή να τον απλοποιήσουμε) κι αυτό δεν είναι δύσκολο αφού είναι γνωστό ότι ισχύει x2-1=(x-1)(x+1). Ας δούμε τώρα πως θα υπολογιστεί το όριο
![Rendered by QuickLaTeX.com \[\underset{x\to 1}{\mathop{\lim }}\frac{x^2-1}{x-1}=\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-bcf0e1e17ac10cdd32b676e9754fe378_l3.png)
![Rendered by QuickLaTeX.com \[\underset{x\to 1}{\mathop{\lim }}\frac{(x-1)(x+1)}{x-1}=\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-ec82cca5e5e1ff459930ec82764e430e_l3.png)
![Rendered by QuickLaTeX.com \[\underset{x\to 1}{\mathop{\lim }},(x+1)=1+1=2\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-b7bbf83af6d4f476d03c9afdc66283fd_l3.png)
Το παράδειγμα αυτό που λύσαμε ανήκει στην πιο συνηθισμένη κατηγορία ορίων που θα συναντήσετε φέτος και είναι αναγκαίο να επεκταθούμε κι άλλο γι’ αυτό το λόγο κάντε κλικ εδώ και μετά στην καρτέλα «Η Απροσδιόριστη μορφή 0/0» που βρίσκεται λίγο παραπάνω.[/su_tab]
[su_tab title=»Η απροσδιόριστη μορφή 0/0″]
Κατά την αναζήτηση του ορίου μιας κλασματικής συνάρτησης ας την πούμε f σε σημείο α ( ![]() )είναι πιθανό να μηδενίζεται για x=α ο αριθμητής και ο παρονομαστής της συνάρτησης. Σε μια τέτοια περίπτωση ( που ονομάζεται απροσδιόριστη μορφή 0/0) δεν μπορούμε να υπολογίσουμε το όριο από τη συνάρτηση που μας έχουν δώσει κι έτσι καταφεύγουμε στο να υπολογίσουμε το όριο αφού πρώτα απλοποιήσουμε την f . Το πως το καταφέρνουμε αυτό εξαρτάται από τη συνάρτηση που μας έχει δοθεί και θα το δούμε σε παραδείγματα παρακάτω. Η βασική ιδέα όμως είναι κοινή και απλή:
)είναι πιθανό να μηδενίζεται για x=α ο αριθμητής και ο παρονομαστής της συνάρτησης. Σε μια τέτοια περίπτωση ( που ονομάζεται απροσδιόριστη μορφή 0/0) δεν μπορούμε να υπολογίσουμε το όριο από τη συνάρτηση που μας έχουν δώσει κι έτσι καταφεύγουμε στο να υπολογίσουμε το όριο αφού πρώτα απλοποιήσουμε την f . Το πως το καταφέρνουμε αυτό εξαρτάται από τη συνάρτηση που μας έχει δοθεί και θα το δούμε σε παραδείγματα παρακάτω. Η βασική ιδέα όμως είναι κοινή και απλή:
από τη στιγμή που βλέπουμε ότι αν θέσουμε x=α στη συνάρτηση μηδενίζεται ο αριθμητής της και ο παρονομαστής της είμαστε σίγουροι ότι και στον αριθμητή αλλά και στον παρονομαστή είναι «κρυμμένος» ο παράγοντας x-α. Σκοπός είναι να τον «εμφανίσουμε» πάνω και κάτω στο κλάσμα έτσι ώστε να τον απλοποιήσουμε (να τον «εξαφανίσουμε» γιατί αυτός ευθύνεται για το 0/0). Μετά την απλοποίηση αυτή είμαστε σε θέση να υπολογίσουμε πολύ απλά το όριο αντικαθιστώντας όπου x το α.
Για να δούμε όμως αναλυτικά πως θα εμφανίσουμε το x-α θα χωρίσουμε τη διαδικασία σε δύο περιπτώσεις. Στην περίπτωση που οι όροι του κλάσματος είναι πολυώνυμα και στην περίπτωση που στο κλάσμα έχουμε τετραγωνική ρίζα. Κάντε κλικ στις παρακάτω μπάρες να δείτε λυμένα βασικά παραδείγματα με την απαραίτητη μεθοδολογία
[wpspoiler name=»Πολυώνυμα»]
Δίνεται η συνάρτηση ![]() . Να βρεθεί το όριο
. Να βρεθεί το όριο ![]() .
.
Λύση: Παρατηρούμε ότι ο παρονομαστής για x=1 μηδενίζεται (2.12-2=2-2=0). Είμαστε σίγουροι ότι και ο αριθμητής μηδενίζεται για x=1 αλλά το τσεκάρουμε (13-12+1-1=0). Τώρα κάνουμε γινόμενο τον αριθμητή και τον παρονομαστή (μπορείτε να θυμηθείτε την παραγοντοποίηση εδώ):
x3-x2+x-1=(x3-x2)+(x-1)[ref] κάναμε ομαδοποίηση[/ref]=x2(x-1)+(x-1)=(x-1)(x2+1). Βλέπουμε ότι εμφανίστηκε το x-1 άρα είμαστε εντάξει
2x2-2=2(x2-1)=2(x-1)(x+1)[ref]κοινός παράγοντας και διαφορά τετραγώνων[/ref] κι εδώ εντάξει, οπότε:
![]()
επομένως
![]()
Όπως βλέπουμε αν έχουμε υπόψη μας τι ακριβώς θέλουμε (να εμφανίσουμε τον παράγοντα x-1 και να τον απλοποιήσουμε) ο υπολογισμός ενός ορίου είναι εύκολη υπόθεση. Κι επειδή το μάθημα αυτό αφορά και μαθητές θεωρητικής κατεύθυνσης που ίσως αντιμετωπίζουν κάποιες δυσκολίες στην παραγοντοποίηση θα σας προτείνω κι έναν άλλο τρόπο που θεωρώ ευκολότερο και ίσως πιο σύντομο, το σχήμα Horner που διδαχθήκαμε στη Β΄τάξη του Λυκείου. Ας δούμε λοιπόν την ίδια άσκηση λυμένη με αυτή τη μέθοδο:
Για να κάνω γινόμενο τον αριθμητή x3-x2+x-1 κάνω σχήμα Horner με τον αριθμό 1
| 1 | -1 | 1 | -1 | 1 |
| 1 | 0 | 1 | ||
| 1 | 0 | 1 | 0 |
Η γαλάζια περιοχή περιέχει τους συντελεστές του πολυωνύμου x3-x2+x-1 που θέλω να κάνω γινόμενο
Η πορτοκαλί περιοχή θα έχει πάντα τον αριθμό στον οποίο τείνει το x (εδώ είναι το 1)
Η ροζ περιοχή θα είναι πάντα 0
Η πράσινη περιοχή μας δίνει τους συντελεστές του πολυωνύμου που θα μείνει όταν απλοποιηθεί το «ενοχλητικό» x-1. Έτσι η νέα μας συνάρτηση θα έχει αριθμητή τον x2+1 αφού το από το σχήμα Horner προκύπτει ότι x3-x2+x-1=(x-1)(x2+1) και το x-1 θα απλοποιηθεί.
Με την ίδια διαδικασία βρίσκω τον νέο παρονομαστή της συνάρτησης
| 2 | 0 | -2 | 1 |
| 2 | 2 | ||
| 2 | 2 | 0 |
οπότε ο παρονομαστής 2x2-2(το γαλάζιο) θα γίνει 2x+2(το πράσινο), αφού από το σχήμα Horner προκύπτει 2x2-2=(x-1)(2x+2) και το x-1 θα απλοποιηθεί.
Τελικά η συνάρτηση f θα γίνει
![]()
κι επομένως το όριο είναι
![]()
Το να ξεφύγεις από την απροσδιόριστη μορφή 0/0 στην περίπτωση που στη συνάρτηση έχεις πολυώνυμο το σχήμα Horner είναι το πιο εύκολο. Το δύσκολο είναι να το περιγράψω πλήρως μέσα από αυτό το άρθρο γι’ αυτό αν κάπου σας μπέρδεψα ζητήστε από τον καθηγητή σας να σας το θυμίσει (είναι υπόθεση δύο λεπτών) ή στείλτε μου μήνυμα να λύσουμε ότι απορία έχετε. Καλού κακού όμως θα λύσουμε ένα παράδειγμα ακόμη:
Να βρεθεί το ![]() .
.
Λύση: Για x=2 μηδενίζονται παρονομαστής και αριθμητής άρα πρέπει να εξαλειφθεί ο παράγοντας x-2.
Στον παρονομαστή υπάρχει το x-2 άρα δεν χρειάζεται να κάνουμε κάτι.
Στον αριθμητή θα κάνουμε σχήμα Horner με το 2 γιατί το x τείνει στο 2,
| 2 | -3 | -2 | 2 |
| 4 | 2 | ||
| 2 | 1 | 0 |
οπότε 2x2-3x-2=(x-2)(2x+1) άρα
![]()
![]()
![]()
[wpspoiler name=»Ριζικά»]
- Για να ξεφύγω από το 0/0 όταν το x τείνει στο α, πρέπει να «εμφανίσω» και μετά να «εξαφανίσω» το x-α από αριθμητή & παρονομαστή
Έστω ότι έχουμε τη συνάρτηση ![]() και θέλουμε να βρούμε το όριο της όταν το τείνει στο 5. Παρατηρούμε ότι για x=5 μηδενίζονται παρονομαστής και αριθμητής, πράγμα που σημαίνει ότι έχω απροσδιόριστη μορφή 0/0, και σύμφωνα με τα όσα έχουμε πει μέχρι τώρα στον αριθμητή αλλά και στον παρονομαστή της συνάρτησης υπάρχει ο παράγοντας x-5 ο οποίος ευθύνεται για τα μηδενικά. Εγώ πρέπει λοιπόν να τον «εμφανίσω» για να τον «εξαφανίσω» . Ευτυχώς στο παράδειγμά μας θα πρέπει να ασχοληθούμε μόνο με τον αριθμητή αφού στον παρονομαστή υπάρχει το x-5 και δεν χρειάζεται να κάνω κάτι. Ο αριθμητής όμως δεν είναι πολυώνυμο για να χρησιμοποιήσω σχήμα Horner ή έστω τους κανόνες της παραγοντοποίησης που έχουμε μάθει μέχρι τώρα. Υπάρχουν αρκετά «κόλπα» για να καταφέρουμε αυτό που θέλουμε αλλά θα αναφερθώ πρώτα στο πιο συνηθισμένο:
και θέλουμε να βρούμε το όριο της όταν το τείνει στο 5. Παρατηρούμε ότι για x=5 μηδενίζονται παρονομαστής και αριθμητής, πράγμα που σημαίνει ότι έχω απροσδιόριστη μορφή 0/0, και σύμφωνα με τα όσα έχουμε πει μέχρι τώρα στον αριθμητή αλλά και στον παρονομαστή της συνάρτησης υπάρχει ο παράγοντας x-5 ο οποίος ευθύνεται για τα μηδενικά. Εγώ πρέπει λοιπόν να τον «εμφανίσω» για να τον «εξαφανίσω» . Ευτυχώς στο παράδειγμά μας θα πρέπει να ασχοληθούμε μόνο με τον αριθμητή αφού στον παρονομαστή υπάρχει το x-5 και δεν χρειάζεται να κάνω κάτι. Ο αριθμητής όμως δεν είναι πολυώνυμο για να χρησιμοποιήσω σχήμα Horner ή έστω τους κανόνες της παραγοντοποίησης που έχουμε μάθει μέχρι τώρα. Υπάρχουν αρκετά «κόλπα» για να καταφέρουμε αυτό που θέλουμε αλλά θα αναφερθώ πρώτα στο πιο συνηθισμένο:
Κάνουμε χρήση της γνωστής ταυτότητας «διαφορά τετραγώνων». Ας την θυμηθούμε ![]() . Την ταυτότητα αυτή μπορούμε να την χρησιμοποιήσουμε και με αυτές τις μορφές:
. Την ταυτότητα αυτή μπορούμε να την χρησιμοποιήσουμε και με αυτές τις μορφές:
-
![Rendered by QuickLaTeX.com \[(\sqrt{A}-\sqrt{B})(\sqrt{A}+\sqrt{B})=(\sqrt{A})^2-(\sqrt{B})^2\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-14df396e773f6dfd4a5fce0934ba0cea_l3.png)
ή ακόμη καλύτερα
![Rendered by QuickLaTeX.com \[(\sqrt{A}-\sqrt{B})(\sqrt{A}+\sqrt{B})=A-B\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-dce0e83c3fbe2e70ad3bd1364a7b6354_l3.png)
-
![Rendered by QuickLaTeX.com \[(\sqrt{A}-B)(\sqrt{A}+B)=A-B^2\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-890c6d5e3b4b35cd7ded4730b24710c4_l3.png)
-
![Rendered by QuickLaTeX.com \[(A-\sqrt{B})(A+\sqrt{B})=A^2-B\]](http://users.sch.gr/dpanagiotis/wp-content/ql-cache/quicklatex.com-2370eae11a90ffd7df8a13628462b01e_l3.png)
Για να δούμε τώρα τι κερδίζουμε από αυτό; Όταν θα μας τυχαίνει μία από τις παραστάσεις που βρίσκονται στις παραπάνω παρενθέσεις εμείς θα πολλαπλασιάζουμε αριθμητή αλλά και παρονομαστή με την διπλανή παρένθεση (λέγεται «συζυγής παράσταση» π.χ. η συζυγής παράσταση της ![]() είναι η
είναι η ![]() ) ώστε σύμφωνα με την ταυτότητα να φύγουν οι ρίζες. Ας το δούμε όμως στη πράξη, στη συνάρτηση f έχω την παράσταση
) ώστε σύμφωνα με την ταυτότητα να φύγουν οι ρίζες. Ας το δούμε όμως στη πράξη, στη συνάρτηση f έχω την παράσταση ![]() η συζυγής παράσταση αυτής είναι η
η συζυγής παράσταση αυτής είναι η ![]() πολλαπλασιάζω λοιπόν αριθμητή και παρονομαστή με αυτή
πολλαπλασιάζω λοιπόν αριθμητή και παρονομαστή με αυτή
![]()
![]()
![]()
![]()
οπότε αφού καταφέραμε και διώξαμε το x-5 μπορούμε να υπολογίσουμε το όριο
![]()
Ένα παράδειγμα ακόμη για να το καταλάβουμε καλύτερα. Να βρεθεί το ![]()
Λύση: Βάζοντας όπου h το 0 παίρνουμε 0/0. Φταίει ο παράγοντας h-0, δηλαδή το h. Κάτω το βλέπουμε και δεν κάνουμε τίποτα. Πάνω έχουμε ![]() η συζυγής της είναι η
η συζυγής της είναι η ![]() με την οποία πολλαπλασιάζω πάνω και κάτω και παίρνω
με την οποία πολλαπλασιάζω πάνω και κάτω και παίρνω
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Κι εδώ τελειώνουν οι περιπτώσεις υπολογισμού ορίων που μπορεί να συναντήσει ένας μαθητής Γ΄Λυκείου στα Μαθηματικά της Γενικής Παιδείας (για την κατεύθυνση έχουμε πολλά να πούμε ακόμη). Καταλαβαίνω ότι το άρθρο είναι τεράστιο, θα μπορούσε να είχε γίνει τριλογία, αλλά θεώρησα καλύτερο να υπάρχουν όλες οι περιπτώσεις μαζί για να έχετε μια ολοκληρωμένη εικόνα. Προτείνω να το διαβάσετε περισσότερες από μία φορά και εξασκηθείτε με τις ασκήσεις που σας δίνω στο παρακάτω link.[/wpspoiler]
Επιστροφή^^^
[/su_tab]
[/su_tabs]
[wpspoiler name=»Δείτε την μεθοδολογία» style=»wpui-quark»]
[/wpspoiler]



Καλημέρα
Θα ήθελα την βοήθεια σας για το παρακάτω όριο lim x τείνει στο 2 8/(χ-2) ^2
Ευχαριστώ
Κωνσταντίνε το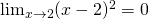 πράγμα που σημαίνει ότι όσο το χ πλησιάζει στο 2 τόσο πιο πολύ το
πράγμα που σημαίνει ότι όσο το χ πλησιάζει στο 2 τόσο πιο πολύ το 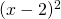 πλησιάζει στο 0. Όμως το ότι «πλησιάζει στο 0» σημαίνει οτι δεν 0 αλλά κάποιος αριθμός πολύ πολύ κοντά στο 0. Αυτός ο αριθμός όμως θα είναι σίγουρα θετικός αφού η παράσταση
πλησιάζει στο 0. Όμως το ότι «πλησιάζει στο 0» σημαίνει οτι δεν 0 αλλά κάποιος αριθμός πολύ πολύ κοντά στο 0. Αυτός ο αριθμός όμως θα είναι σίγουρα θετικός αφού η παράσταση 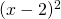 είναι μονίμως θετική ( αφού είναι υψωμένη στο τετράγωνο), άρα θα είναι ένας υπερβολικά μικρός θετικός αριθμός. Έτσι λοιπόν το κλάσμα
είναι μονίμως θετική ( αφού είναι υψωμένη στο τετράγωνο), άρα θα είναι ένας υπερβολικά μικρός θετικός αριθμός. Έτσι λοιπόν το κλάσμα 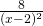 θα είναι πάντα θετικός αριθμός. Όταν όμως το χ θα πλησιάζει το 2 το κλάσμα θα έχει αριθμητή το 8 και παρονομαστή όπως είπαμε έναν υπερβολικά μικρό θετικό αριθμό. Αυτό σημαίνει ότι το κλάσμα θα είναι ένας τεράστια μεγάλος θετικός αριθμός (γιατί, σου θυμίζω ότι, όσο μικραίνει ο παρονομαστής ενός κλάσματος τόσο μεγαλώνει το κλάσμα), δηλαδή το όριο θα είναι
θα είναι πάντα θετικός αριθμός. Όταν όμως το χ θα πλησιάζει το 2 το κλάσμα θα έχει αριθμητή το 8 και παρονομαστή όπως είπαμε έναν υπερβολικά μικρό θετικό αριθμό. Αυτό σημαίνει ότι το κλάσμα θα είναι ένας τεράστια μεγάλος θετικός αριθμός (γιατί, σου θυμίζω ότι, όσο μικραίνει ο παρονομαστής ενός κλάσματος τόσο μεγαλώνει το κλάσμα), δηλαδή το όριο θα είναι 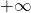 . Τώραόσον αφορά το πως θα γράψεις τη λύση προτείνω το εξής:
. Τώραόσον αφορά το πως θα γράψεις τη λύση προτείνω το εξής: